|
|
|
CHAPTER 7: REGIONAL ANALYSIS |
|
"In most natural systems, drainage from the uplands finds its way into rivers and then into the ocean. Ocean disposal is nature's way of moving dissolved salts out of the landscape." Jan van Schilfgaarde (1990) |
|
This chapter is divided into three sections. Section 7.1 describes joint probability distributions, including marginal distributions and conditional probability. Section 7.2 describes the techniques of regression analysis. Section 7.3 presents selected techniques for regional analysis of flood and rainfall characteristics. |
7.1 JOINT PROBABILITY
|
|
In engineering hydrology, regional analysis encompasses the study of hydrologic phenomena with the aim of developing mathematical relations to be used in a regional context. Generally, mathematical relations are developed so that information from gaged or long-record catchments can be readily transferred to neighboring ungaged or short-record catchments of similar hydrologic characteristics. Other applications of regional analysis include regression techniques used to develop empirical (i.e., parametric) equations applicable within a broad geographical region. Regional analysis makes use of statistics and probability, including frequency analysis (Chapter 6) and joint probability distributions.
Joint Probability Distributions
Probability distributions possessing one random variable (X) were discussed in Chapter 6. These are called univariate distributions. Probability distributions with two random variables, X and Y, are called bivariate or joint distributions. A joint distribution expresses in mathematical terms the probability of occurrence of an outcome consisting of a pair of values of X and Y. In statistical notation, P(X = xi, Y = yj) is the probability P that the random variables X and Y will take on the outcomes xi and yj simultaneously. A shorter notation is P(xi, yj).
For xi (1, 2, ... , n), and yj (1, 2, ... , m), the sum of the probabilities of all possible outcomes is equal to unity:
|
n m Σ Σ P(xi, yj) = 1 i = 1 j = 1 | (7-1) |
A classical example of joint probability is that of the outcome of the cast of two dice, say A and B. Intuitively, the probability of getting a 1 for A and a 1 for B is P(A = 1, B = 1) = 1/36; see Fig. 7-1. In total, there are 6 × 6 = 36 possible outcomes, and each one of them has the same probability: 1/36 (assuming, of course, that the dice are not loaded). This distribution is referred to as the bivariate uniform distribution because each outcome has a uniform and equal probability of occurrence. The sum of the probabilities of all possible outcomes is confirmed to be equal to 1.
Figure 7-1 Joint probability: The outcome of two dice. |
Joint cumulative probabilities are defined in a similar way as for univariate probabilities:
|
k l F(xk, yl) = Σ Σ P(xi, yj) i = 1 j = 1 | (7-2) |
in which F(xk, yl) is the joint cumulative probability. Continuing with the example of the two dice, the probability of A being ≤ 3 and B being ≤ 3 is the sum of all the individual probabilities, for all combinations of i and j, as i varies from 1 to 3, and as j varies from 1 to 3; i.e., 3 × 3 = 9 possible combinations, resulting in a probability equal to 9 × (1/36) = 1/4.
Marginal Probability Distributions
Marginal probability distributions are obtained by summing up P(xi, yj) over all values of one of the variables, for instance, X. The resulting (marginal) distribution is the probability distribution of the other variable, in this case Y without regard to X. Marginal distributions are univariate distributions obtained from bivariate distributions. In statistical notation, the marginal probability distribution of X is:
|
m P(xi) = Σ P(xi, yj) j = 1 | (7-3) |
Likewise, the marginal distribution of Y is:
|
n P(yj) = Σ P(xi, yj) i = 1 | (7-4) |
The example of the two dice A and B may be used to illustrate the concept of marginal probability. Intuitively, the probability of A being equal to 1, regardless of the value of B, is 6 × (1/36) = 1/6. Likewise, the probability of B being equal to 4, regardless of the value of A, is also 1/6. Notice that the joint probabilities (1/36) of each one of all 6 possible outcomes have been summed in order to calculate the marginal probability.
Marginal cumulative probability distributions are obtained by combining the concepts of marginal and cumulative distributions. In statistical notation, the marginal cumulative probability distribution of X is:
|
k m F(xk) = Σ Σ P(xi, yj) i = 1 j = 1 | (7-5) |
Likewise, the marginal distribution of Y is:
|
n l F(yl) = Σ Σ P(xi, yj) i = 1 j = 1 | (7-6) |
The example of the two dice A and B is again used to illustrate the concept of marginal cumulative probability. The probability of A ≤ 2, regardless of the value of B, is: 2 × 6 × (1/36) = 1/3. Likewise, the probability of B ≤ 5, regardless of the value of A, is: 5 × 6 × (1/36) = 5/6. To calculate the marginal cumulative probabilities, the concepts of marginal and cumulative distributions have been combined.
Conditional Probability
The concept of conditional probability is useful in regression analysis and other hydrologic applications. The conditional probability is the ratio of joint and marginal probabilities. In statistical notation:
|
P(x,y) P(x |y) = ________ P(y) | (7-7) |
in which P(x |y) is the conditional probability of x, given y. Likewise, the conditional probability of y, given x, is:
|
P(x,y) P(y |x) = ________ P(x) | (7-8) |
From Eqs. 7-7 and 7-8, it follows that joint probability is the product of conditional and marginal probabilities.
Joint probability distributions can be expressed as continuous functions.
In this case they are called joint density functions, with the notation f(x,y).
For the conditional density function, the notation is
As with univariate distributions, the moments provide descriptions of the properties of joint distributions. For continuous functions, the joint moment of order r and s about the origin (indicated with ') is defined as follows:
|
∞ ∞ μ'r,s = ∫ ∫ x ry s f (x,y ) dy dx -∞ -∞ | (7-9) |
With r = 1 and s = 0, Eq. 7-9 reduces to the mean of x :
|
∞ ∞ μ'1,0 = ∫ x [ ∫ x ry s f (x,y ) dy ] dx -∞ -∞ | (7-10) |
with the expression between brackets being the marginal PDF of x, or f(x). Therefore, the expression for the mean of x is:
|
∞ μ'1,0 = μx = ∫ x f (x ) dx -∞ | (7-11) |
Similar equations hold for y.
The second moments are usually written about the mean:
|
∞ ∞ μ'r,s = ∫ ∫ ( x - μx )r ( y - μy )s f (x,y ) dy dx -∞ -∞ | (7-12) |
For r = 2 and s = 0, Eq. 7-12 reduces to the variance of x.
Likewise, for r = 0 and s = 2, Eq. 7-12 reduces to the variance of y.
A third type of second moment, i.e., the covariance, arises for r = 1 and
|
∞ ∞ σx,y = ∫ ∫ ( x - μx ) ( y - μy ) f (x, y ) dy dx -∞ -∞ | (7-13) |
in which σx,y is the covariance.
The correlation coefficient is a dimensionless value relating the covariance σx,y and standard deviations σx and σy :
|
σx,y ρx,y = _________ σx σy | (7-14) |
in which ρx,y is the correlation coefficient based on population data. The sample correlation coefficient is:
|
sx,y rx,y = ________ sx sy | (7-15) |
The calculation of sample correlation coefficient rx,y including the sample covariance sx,y is illustrated by Example 7-1.
The correlation coefficient is a measure of the linear dependence between x and y.
It varies in the range of -1 to + 1.
A value of ρ (or r ) close to or equal to 1 indicates a strong linear dependence
between the variables, with large values of x associated with large values of y,
and small values of x with small values of y.
A value of ρ (or r ) close to or equal to -1 indicates a correlation such that large values of x are associated with small values of y and vice versa.
A value of ρ = 0
Example 7-1.
The monthly flows of the North Fork and South Fork tributaries of a certain stream (see, for example, Fig. 7-2) have the following joint probability distribution f (x, y) (expressed as mean value in each class) (Note that
1 hm3 = 1 million cubic meters):
Calculate the marginal distributions, means, variances, standard deviations, covariance, and correlation coefficient for this joint distribution.
The North Fork marginal distribution, f(x), is obtained by summing up the joint probabilities across y.
Therefore:
Likewise, the South Fork marginal distribution, f(y), is obtained by summing up the joint probabilities across x:
The means are the first moments of the marginal distributions with respect to the origin:
The variances are the second moments of the marginal distributions with respect to the means:
sx2 = Σ ( x - x̄ )2 f (x) Therefore:
sx = 95.26 hm3
Likewise, for y:
sy = 97.42 hm3
The covariance is the second moment of the joint distribution:
The correlation coefficient is rx,y = sx,y / (sx sy) = 7785 / (95.26 × 97.42) = 0.839.
ONLINE CALCULATION. Using
ONLINE TWOD CORRELATION,
the answer
is: Correlation coefficient rx,y = 0.839, confirming the hand calculation.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
Figure 7-2 North Fork and South Fork, Little Butte Creek, Oregon.
Bivariate Normal Distribution
Among the many joint probability distributions, the bivariate normal distribution is important in hydrology because it is the foundation of regression theory. The bivariate normal probability distribution is [12]:
| f (x , y) = K e M | (7-16) |
in which x and y are the random variables, and K and M are coefficient and exponent. respectively, defined as follows:
|
1 K = _________________________ 2 π σx σy (1 - ρ2)1/2 | (7-17) |
|
1 M = - ___________ [ A ] 2 (1 - ρ2) | (7-18a) |
in which:
|
x - μx x - μx y - μy y - μy A = ( _________ )2 - 2 ρ ( _________ ) ( _________ ) + ( _________ )2 σx σx σy σy | (7-18b) |
The distribution has five parameters: the means μx and μy, the standard deviations σx and σy, and the correlation coefficient ρ.
Following Eq. 7-8, the conditional distribution is obtained by dividing the bivariate normal (Eq. 7-16) by the univariate normal (Eq. 6-7), to yield
|
f
(x, y) K = _________ = K' eM' f (x) | (7-19) |
in which K' and M' are coefficient and exponent, respectively, defined as follows:
|
1 K' = _____________________ σy [2 π (1 - ρ2)]1/2 | (7-20) |
|
1
σy M' = - ________________ [ (y - μy) - ρ ______ (x - μx) ]2 2 σy2 (1 - ρ2) σx | (7-21) |
By inspection of Eqs. 7-20 and 7-21, and comparison with Eq. 6-7, it is concluded that the conditional distribution is also normal, with mean and variance:
|
σy μy|x = μy - ρ _____ (x - μx) σx | (7-22) |
| σe2 = σy2 (1 - ρ2) | (7-23) |
Equations 7-22 and 7-23 are useful in regression analysis. Equation 7-22 expresses the linear dependence between x and y. The slope of the regression line is [ρ σy/σx]. Likewise, ρ is the fraction of the original variance explained or removed by the regression. In other words, the variance of the conditional distribution is less than or equal to the variance of y without regard to x, and it depends on the value of the correlation coefficient ρ. For ρ = 1, all the variance is removed, and the error of the predictive equation (i.e., the error of the regression) is reduced to zero. For ρ = 0, none of the original variance is removed, and σe remains equal to σy.
7.2 REGRESSION ANALYSIS
|
|
A fundamental tool of regional analysis is the equation relating two or more hydrologic variables. The variable for which values are given is called the predictor variable. The variable for which values must be estimated is called the criterion variable [7]. The equation relating criterion variable to one or more predictor variables is called the prediction equation.
The objective of regression analysis is to evaluate the parameters of the prediction equation relating the criterion variable to one or more predictor variables. The predictor variables are those whose variation is believed to cause or agree with variation in the criterion variable.
Correlation provides a measure of the goodness of fit of the regression. Therefore, while regression provides the parameters of the prediction equation, correlation describes its quality. The distinction between correlation and regression is necessary because the predictor and criterion variables cannot be switched unless the correlation coefficient is equal to 1. Stated in other terms, if a criterion variable Y is regressed on a predictor variable X, the regression parameters cannot be used to express X as a function of Y, unless the correlation coefficient is 1. In hydrologic modeling, regression analysis is useful in model calibration; correlation is useful in model formulation and verification.
The principle of least squares is used in regression analysis as a means of obtaining the best estimates of the parameters of the prediction equation. The principle is based on the minimization of the sum of the squares of the differences between observed and predicted values. The procedure can be used to regress one criterion variable on one or more predictor variables.
One-Predictor-Variable Regression
Assume a predictor variable x, a criterion variable y, and a set on n paired observations of x and y. In the simplest linear case, the line to be fitted has the following form:
| y' = α + βx | (7-24) |
in which y' is an estimate of y, and α and β are parameters to be determined by regression.
In the least squares procedure, values of the intercept α and slope β are sought such that y' is the best estimate of y. For this purpose, the sum of the squares of the differences between y and y' are minimized as follows:
| Σ ( y - y' )2 = Σ [ y - ( α + βx ) ] 2 | (7-25) |
in which the symbol Σ indicates the sum of all values from i = 1 to i = n.
Setting the partial derivatives equal to zero:
|
∂ ____ { Σ [ y - ( α + βx ) ] 2 } = 0 ∂α | (7-26) |
|
∂ ____ { Σ [ y - ( α + βx ) ] 2 } = 0 ∂β | (7-27) |
This leads to the normal equations:
| Σ y - nα - β Σ x = 0 | (7-28) |
| Σ xy - α Σ x - β Σ x2 = 0 | (7-29) |
Solving Eqs. 7-28 and 7-29 simultaneously gives:
|
Σ xy - ( Σ x Σ y ) / n β = ________________________ Σ x2 - ( Σ x )2 / n | (7-30) |
|
Σ y
- β Σ x α = __________________ n | (7-31) |
Since the slope of the regression line is: β = ρ σy /σx,
the estimate from sample data is:
|
sx r = β ____ sy | (7-32) |
The standard error of estimate of the correlation is the square root of the variance of the conditional distribution:
|
1 se = [ ______ Σ (y - y' )2 ] 1/2 n - 2 | (7-33) |
in which n - 2 is the number of degrees of freedom, i.e., the sample size minus the number of unknowns.
Alternatively, the standard error of estimate can be estimated from the variance of the conditional distribution, Eq. 7-23. For calculations based on sample data, the standard error of estimate is:
|
n - 1 se = sy [ ______ (1 - r 2) ] 1/2 n - 2 | (7-34) |
Nonlinear Equations.
Equations 7-30 and 7-31 can also be used to fit power functions of the type
Example 7-2.
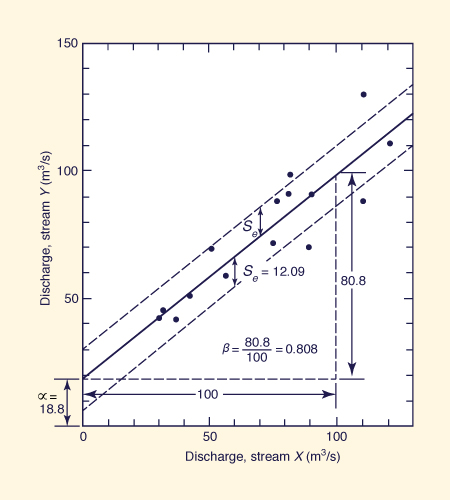
Find the regression equation linking the low flows (annual minima series) of streams X and Y shown in Cols. 2 and 3 of Table 7-1.
Calculate the linear regression parameters α and β, the correlation coefficient, and the standard error of estimate.
Summing up the values of Cols. 2 and 3, and dividing by n = 15, the means are obtained: x̄ = 72 m3/s and ȳ = 77 m3/s.
Columns 4 and 5 show the square of the deviations from the means.
Summing up Cols. 4 and 5, dividing the sums by (n - 1) = 14, and taking the square roots, the standard deviations sx = 29.568 m3/s and sy = 26.589 m3/s are obtained.
Column 6 shows the x2 values, and Col. 7, the xy values.
The sum of these values is: Σ x2 = 90,000 and Σ xy = 93,056.
Using Eq. 7-30: β = [93,056 - (1,080 × 1,155)/ 15 ] / [ 90,000 - (1,080 × 1,080)/ 15] = 0.80849.
Using Eq. 7-31: α = [1155 - (0.8085 × 1080)] / 15 = 18.7882.
Using Eq. 7-32, the correlation coefficient is: r = 0.80849 × 29.568 / 26.589 = 0.899.
Using Eq. 7-34, the standard error of estimate is: se = 26.589 × [(14/13) (1 - 0.8992)] 1/2 = The data and regression line are plotted in Fig. 7-3.
ONLINE CALCULATION. Using
ONLINEREGRESSION11,
the answer
is: α = 18.7882;
Figure 7-3 X-Y ( One-predictor-variable) regression: Example 7-2.
Multiple Regression
The extension of the least squares technique to more than one predictor variable is referred to as multiple regression.
In the case of two predictor variables, x1 and x2, with criterion variable y and a set of n observations of y, x1 and x2, the line to be fitted is:
in which x1 and x2 are measured values and y' is an estimate of y.
As with the two variable case, values of the intercept α and slopes β1 and β2 are sought such that y' is the best estimate of y.
For this purpose, the sum of the squares of the differences between y and y' are minimized.
Setting the partial derivatives with respect to α, β1 and β2 equal to zero leads to the normal equations:
Solving Eqs. 7-37 to 7-39 simultaneously:
As in the case of the one-predictor-variable regression, the standard error of estimate of the correlation is the square root of the variance of the conditional distribution:
in which n - 3 is the number of degrees of freedom.
Alternatively, the standard error of estimate can be estimated from the variance of the conditional distribution.
For calculations based on sample data, the standard error of estimate is:
in which R = multiple regression coefficient, or coefficient of multiple determination, calculated as follows [8]:
in which SSE = error sum of squares, defined as
and SSTO = total sum of squares, defined as
Nonlinear Multiple Regression
Equations 7-40 to 7-42 can also be used to fit equations of the type:
First, this equation is linearized by taking the logarithms:
With u = log x1 v = log x2, and w = log y, this equation is: w = log a + bu + cv.
The variables u, v, and w are used in Eqs. 7-40 to 7-42 instead of x1, x2, and y, respectively.
Then α = log a, β1 = b1, β2 = b2, and the regression equation is:
Multiple regression analysis involving more than two predictor variables is based on the same least squares principle as in the cases shown here.
Library programs are usually available to perform the large amount of computations involved.
7.3 REGIONAL ANALYSIS
Peak Flow Based on Catchment Area
The earliest approach to regionalization of hydrologic properties was to assume that peak flow is related to catchment area and to perform a regression to determine the parameters.
The equation is of the following form:
in which Qp = peak flow; A = catchment area; and c and m are regression parameters.
In nature, as catchment area increases, the spatially averaged rainfall intensity decreases, and consequently peak flow does not increase as fast as catchment area.
Therefore, the exponent m in Eq. 7-51 always less than 1, usually in the range 0.4 to 0.9 [5, 10] .
Practical examples of the use of this method are given in Section 14.6.
Other formulas relating peak flow to catchment area are the following:
in which a, b, c, d, m, and n are parameters determined from statistical analysis of measured data and are applicable on a regional basis, i.e., for neighboring watersheds of similar physiographic, vegetative, and land use patterns.
The Creager curves (Fig. 2-73) are an example of Eq. 7-52 [3]. Equation 7-53 been used in regional flood studies in the Southwest [2, 6, 9], whereas Eq. 7-54 appears to be typical of European practice [5].
In principle, none of these equations accounts explicitly for flood frequency, being limited to providing a maximum flow.
The effect of flood frequency, however, can be accounted for by varying the parameters (Section 14.6).
Index-Flood Method
The index-flood method is used to determine the magnitude and frequency of peak flows for catchments of any size, whether gaged or ungaged, located within a hydrologically homogeneous region, i.e. , a region with similar hydrologic characteristics [1, 4].
The application of the index-flood method consists of developing two curves.
The first curve depicts the mean annual flood (i.e., that corresponding to the 2.33-y frequency) versus catchment area.
The second curve shows peak flow ratio versus frequency.
The peak flow ratio is the ratio of peak flow for a given frequency to the mean annual flood.
Using these two curves, a flood-frequency curve may be developed for any catchment in the region.
The procedure consists of the following steps:
Mean Annual Flood
The magnitude of the mean annual flood is a function of several physiographic and meteorologic factors.
The physiographic factors that may influence the mean annual flood are the following:
The meteorologic factors include:
Of the above factors, drainage area is the most important and the one most readily available.
Measuring the other factors is usually more difficult.
For instance, channel storage has an important effect but cannot be measured directly.
For practical use, a regression of mean annual flood on catchment area is usually sufficient.
Alternatively, equations relating mean annual flood to catchment characteristics other than area can be determined by using multiple regression techniques.
Regional Frequency Curve.
The procedure to develop a regional frequency curve by the index-flood method consists of the following steps:
Assemble the records (annual exceedence or annual maxima series) of several stations (usually 10 to 15), each having more than 5 y of record.
Select a time base common to all the stations (common base period of analysis) in order to eliminate the effect of variability with time.
For each i th station, rank the records in descending order and compute return periods using a plotting position formula such as Weibull's (Eq. 6-26).
For each i th station, plot the annual flows versus return periods on extreme value probability paper and fit a line visually to determine the frequency curve.
For each i th station, determine the mean annual flood, that is, the peak flow corresponding to the 2.33-y frequency.
Choose several frequencies, and for each i th station and j th frequency calculate the peak flow ratio, i.e., the ratio of peak flow for the j th frequency to the mean annual flood.
For each j th frequency, determine the median value of peak flow ratios for all stations, that is, the median peak flow ratio.
Plot median peak flow ratios versus frequencies on extreme value probability paper and draw a line of best fit to obtain a regional flood frequency curve for the given data.
Test of Hydrologic Homogeneity.
The index-flood method includes a test of regional hydrologic homogeneity.
Any station not passing this test should be excluded from the set.
The test procedure consists of the following steps [4]:
For each i th station, use its frequency curve to determine the 2.33-y and the 10-y floods.
For each i th station, calculate the 10-y peak flow ratio, i.e., the ratio of the 10-y flood to the 2.33-y flood.
Calculate the average of the 10-y peak flow ratios for all stations.
For each i th station, multiply the 2.33-y flood by the average 10-y peak flow ratio to obtain an adjusted 10-y peak flow.
For each i th station, use its frequency curve to determine the return period Ti for the adjusted 10-y peak flow.
For each i th station, plot the return period Ti versus the length of record n, in years, in Fig. 7-4.
Points located within the confidence limits (solid lines) are considered to be hydrologically homogeneous.
Points lying outside of the solid lines should not be used in the calculation of the median peak flow ratio (step 7 of the index-flood method).
Figure 7-4 Homogeneity test chart for index-flood method [4].
Limitations of the Index-Flood Method.
Benson [1] has noted the following limitations of the index-flood method:
The mean annual flood for stations with short periods of record may not be typical, which means that the peak flow ratios of different return periods may vary widely among stations.
The homogeneity test is used to determine whether the differences in the frequency curves are greater than those that could be attributed to chance alone.
The index-flood test uses the 10-y flow ratio because of the lack of sufficient data
to define the frequency curve adequately at longer return periods.
Studies have shown that although homogeneity may be assumed on the basis of the 10-y peak flow ratio, the individual frequency curves may show wide and sometimes systematic differences at longer return periods.
The method combines frequency curves for all catchment sizes, excluding only the largest.
At the 10-y peak flow ratio level, the effect of catchment size is small and can be neglected. Studies have shown that the peak flow ratios tend to vary inversely with catchment size.
In general, the larger the catchment, the flatter the frequency curve and the lower the peak flow ratios.
The effect of catchment size is particularly marked for floods of long return period.
Example 7-3.
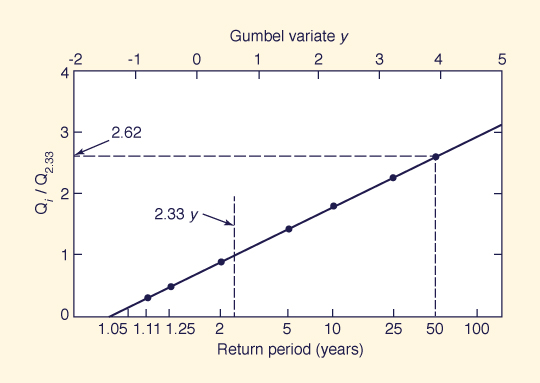
Use the Qi/Q2.33 data for the five stations shown in Table 7-2 to develop a regional flood frequency curve by the index-flood method.
Assuming Q2.33 = 2.5A0.6, in which Q2.33 is in cubic meters per second and catchment area A is in square kilometers, calculate the 50-y flood for a 150-km2 catchment based on the regionally developed curve.
The median values are shown at the bottom of each column.
These values are plotted against the return period, as shown in Fig. 7-5.
The fitted line is the regional flood-frequency curve.
For a 150-km2 catchment, the mean annual flood is: 50.5 m3/s.
From Fig. 7-5, the peak flood ratio for the 50-y return period is 2.62.
Therefore, the 50-y flood for this catchment is 132 m3/s.
Figure 7-5 Index-flood method: Example 7-3.
Curves showing the relationship between intensity, duration, and frequency of rainfall (IDF curves) are required for peak flow computations in small catchments (see rational method, Chapter 4).
These curves can be developed using either: (a) depth-duration-frequency data provided by the National Weather Service, or (b) regional or local rainfall intensity-duration data.
The latter procedure is illustrated by the following example.
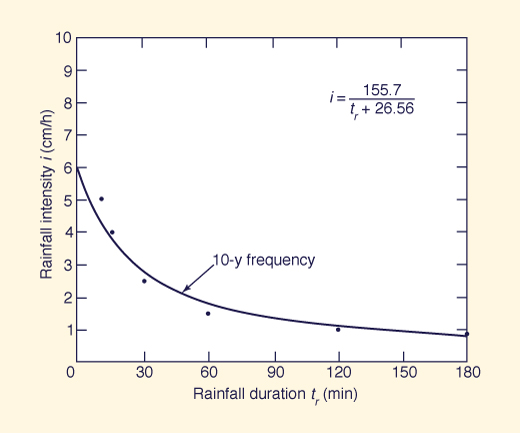
Example 7-4.
Determine the equation relating rainfall intensity and duration for the following 10-y frequency rainfall data.
The data suggest that the relation is of hyperbolic type, with greater intensities associated with shorter durations.
Therefore, an equation of the type of Eq. 2-6 is applicable:
in which a and b are constants to be determined by regression analysis.
This equation can be linearized in the following way:
With y = 1/i, x = tr, α = b/a, and β = 1/a, the application of the regression formulas (Eqs. 7-30 and 7-31) to the data leads to: 1/i = 0.006422 tr, + 0.1706, in which α = 0.1706 and β = 0.006422.
Therefore: a = 155.7 and b = 26.56.
The regression equation is: i = 155.7 / (tr + 26.56).
The data and regression line are shown in Fig. 7-6.
ONLINE CALCULATION. Using
ONLINEREGRESSION15,
the answer
is: a = 155.702;
Figure 7-6 Fitting intensity-duration-frequency curve: Example 7-4.
The U.S. Geological Survey has developed a comprehensive methodology for regional analysis of flood frequency [11].
Details of this method are given in Section 14.6.
QUESTIONS
What is a joint probability? What is a marginal probability?
What is a joint density function? Give an example.
What is a conditional probability? How is it used in regression analysis?
Define covariance.
What is a correlation coefficient?
What is the difference between correlation and regression?
Describe briefly the index-flood method for regional analysis of flood frequency.
PROBLEMS
Using ONLINE TWOD CORRELATION,
calculate the correlation coefficient of the following joint distribution of quarterly flows (expressed as mean values in each class) in streams A and B:
Develop a spread sheet to calculate the regression constants, correlation coefficient, and standard error of estimate of a series of paired flow values X and Y. Test your program using the data of Example 7-2 in the text.
Using the spread sheet developed in Problem 7-2, calculate the regression constants, correlation coefficient, and standard error of estimate for the following paired low-flow series (annual minima):
Verify with ONLINE REGRESSION11.
Modify the spread sheet developed in Problem 7-2 to calculate the regression constants to fit a power function of the following form (Eq. 7-51):
in which Qp = peak discharge; A = drainage area; c and m are coefficient and exponent, respectively.
Using the spread sheet developed in Problem 7-4, fit a power function to the following data:
Verify with ONLINE REGRESSION12.
ONLINE REGRESSION13 solves the two-predictor-variable
linear regression problem (Eq. 7-35). Use this program to determine the regression constants for the following data set:
Use ONLINE REGRESSION14
to solve the two-predictor-variable nonlinear regression problem of Eq. 7-48, for the data of Problem 7-6.
The median Qi/Q2.33 ratios (i = frequency) for 10 stations have been found to be 1.95 for the 10-y frequency and 2.45 for the 50-y frequency.
Use the index-flood method to calculate the 25-y flood for a point in a stream having a 340-km2 catchment and a mean annual flood given by the following formula:
in which Q = flood discharge in cubic meters per second, and A = drainage area in square kilometers.
Modify the spread sheet developed in Problem 7-2 to calculate the regression constants and correlation coefficient to fit intensity-duration-frequency rainfall data. Test your spread sheet using the data of Example 7-4 in the text.
Using ONLINE REGRESSION15 for a hyperbolic regression,
calculate the regression constants a and b (Eq. 7-55) for the following 25-y frequency rainfall data:
REFERENCES
Benson, M. A. (1962). "Evolution of Methods for Evaluating the Occurrence of Floods," U.S. Geological Survey Water Supply Paper No. 1580-A.
Boughton, W. C., and K. G. Renard. (1984). "Flood Frequency Characteristics of Some Arizona Watersheds," Water Resources Bulletin, Vol. 20, No. 5, October, pp. 761- 769.
Creager, W. P., J. D. Justin, and 1. Hinds. (1945). Engineering for Dams. Vol. 1. New York: John Wiley.
Dalrymple, T. (1960). "Flood Frequency Analyses," U.S. Geological Survey Water Supply Paper No. 1543A.
Hall, M. J. (1984). Urban Hydrology. London: Elsevier Applied Science Publishers.
Malvick, A. J. (1980). "A Magnitude-Frequency-Area Relation for Floods in Arizona," Research Report No. 2, College of Engineering, University of Arizona, Tucson.
McCuen, R. H. (1985). Statistical Methods for Engineers. Englewood Cliffs, N.J.: Prentice-Hall.
Neter, J., W. Wasserman, and M. H. Kutner. (1989). Applied Linear Regression Models, Second Edition, Irwin, Homewood, illinois.
Reich. B. M., H. B. Osborn. and M. C. Baker. (1979). "Tests on Arizona New Flood Estimates," in Hydrology and Water Resources in Arizona and the Southwest, University of Arizona, Tucson, Vol. 9.
Roeske, R. H. (1978). "Methods for Estimating the Magn!tude and Frequency of Floods in Arizona," Final Report, ADOT-RS-lS-121, U.S. Geological Survey, Tucson, Arizona.
U.S. Geological Survey. (1994). "Nationwide Summary of U.S. Geological Survey Regional Regression Equations for Estimating Magnitude and Frequency of Floods for Ungaged Sites, 1993" Compiled by M. E. Jennings, W. O. Thomas, and H. C. Riggs, Water-Resources Investigations Report 94-4002, Reston, Virginia.
Viessman, W. Jr., J. W. Knapp, G. L. Lewis, and T. E. Harbaugh, Introduction to Hydrology, 2d. ed, New York: Harper & Row.
Table 7-1 One-Predictor-Variable Regression: Example 7-2.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Year
x
(m3/s)y
(m3/s)( x - x̄ )2
( y - ȳ )2
x2
xy
1973
110
89
1,444
144
12,100
9,790
1974
42
51
900
676
1,764
2,142
1975
75
72
9
25
5,625
5,400
1976
120
112
2,304
1,225
14,400
13,440
1977
89
70
289
49
7,921
6,230
1978
32
45
1,600
1,024
1,024
1,440
1979
37
42
1,225
1,225
1,369
1,554
1980
56
59
256
324
3,136
3,304
1981
82
100
100
529
6,724
8,200
1982
90
92
324
225
8,100
8,280
1983
50
70
484
49
2,500
3,500
1984
30
42
1,764
1,225
900
1,260
1985
81
92
81
225
6,561
7,452
1986
110
130
1,444
2,809
12,100
14,300
1987
76
89
16
144
5,776
6,764
Sum
1,080
1,155
12,240
9,898
90,000
93,056
![]()
y' = α + β1x1 + β2x2
(7-35)
Σ ( y - y' )2 = Σ [ y - (α + β1x1 + β2x2) ] 2
(7-36)
Σ y - nα - β1 Σx1 - β2 Σx2 = 0
(7-37)
Σ yx1 - αΣ x1 - β1 Σ x12 - β2 Σ x1x2 = 0
(7-38)
Σ yx2 - αΣ x2 - β2 Σ x22 - β1 Σ x1x2 = 0
(7-39)
( nΣyx2 - Σy Σx2 )( nΣx1x2 - Σx1 Σx2 ) - [ nΣx22 - (Σx2 )2] [ nΣyx1 - ΣyΣx1]
β1 = ___________________________________________________________________________________
(nΣx1x2 - Σx1Σx2)2 - [nΣx12 - (Σx1)2] [nΣx22 - (Σx2)2]
(7-40)
( nΣyx1 - Σy Σx1 ) - β1 [nΣx12 - (Σx1)2]
β2 = ______________________________________________
nΣx1x2 - Σx1 Σx2
(7-41)
Σy - β1Σx1 - β2Σx2
α = ___________________________
n
(7-42)
1
se = [ _______ Σ (y - y' )2 ] 1/2
n - 3
(7-43)
n - 1
se = sy [ _______ ( 1 - R 2 ) ] 1/2
n - 3
(7-44)
R 2 = 1 - (SSE / SSTO )
(7-45)
SSE = Σ ( y - y' )2
(7-46)
SSTO = Σ ( y - ȳ )2
(7-47)
y = a x1b1 x2b2
(7-48)
log y = log a + b1 log x1 + b2 log x2
(7-49)
y = 10α x1β1 x2β2
(7-50)
Qp = c A m
(7-51)
Qp = c A nA-m
(7-52)
Qp = c A a - b log A
(7-53)
cA
Qp = ______________ + dA
(a + bA ) m
(7-54)
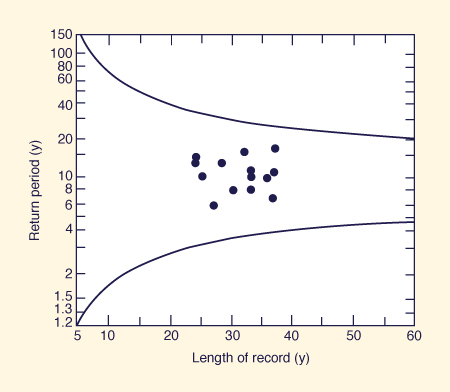
Table 7-2 Index-Flood Method: Example 7-3.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
Station
iQi /Q 2.33 for the j th Return Period (years)
1.11
1.25
2
5
10
25
50
1
0.32
0.49
0.90
1.45
1.82
2.28
2.62
2
0.35
0.51
0.92
1.44
1.79
2.23
2.56
3
0.39
0.55
0.92
1.40
1.73
2.14
2.44
4
0.27
0.45
0.90
1.50
1.88
2.38
2.74
5
0.31
0.50
0.91
1.46
1.84
2.32
2.68
Median
0.32
0.50
0.91
1.45
1.82
2.28
2.62
Rainfall Intensity-Duration-Frequency
Rainfall duration tr (min)
5
10
15
30
60
120
180
Rainfall intensity i (cm/h)
8
5
4
2.5
1.5
1.0
0.8
a
i = ___________
tr + b
(7-55)
1 tr b
___ = ____ + ____
i a a
(7-56)
![]()
State Equations for Regional Flood Frequency
Stream A
(ac-ft)1000
2000
3000
4000
5000
Stream B
(ac-ft)
1000
0.07
0.03
0.02
0.00
0.00
2000
0.03
0.08
0.04
0.03
0.00
3000
0.02
0.04
0.08
0.05
0.02
4000
0.00
0.04
0.08
0.11
0.06
5000
0.00
0.00
0.03
0.08
0.09
Stream X
(m3/s)Stream Y
(m3/s)50
65
66
76
32
45
78
95
12
18
34
50
23
31
50
64
43
67
89
99
76
89
22
33
Qp = cAn
Peak Discharge
(m3/s)Drainage Area
(km2)124
25
254
46
378
78
101
22
678
99
540
89
490
83
267
52
350
73
Y
Time of Concentration
(min)X1
Hydraulic Length
(m)X2
Catchment Slope
(m/m)89
3245
0.008
75
2567
0.011
57
2783
0.009
34
1234
0.015
101
5345
0.006
121
5329
0.007
68
3002
0.008
79
2976
0.010
25
1034
0.018
59
2984
0.010
96
3892
0.007
12
534
0.020
Q 2.33 = 3.93 A 0.75
Duration (min)
5
10
15
30
60
120
180
Intensity (mm/h)
15.5
7.5
6.5
4.5
3.5
2.5
1.5
http://engineeringhydrology.sdsu.edu
140612

