HCA, Capítulo 10, Fundamentos da Hidráulica de Canais, Escoamento Estável Gradualmente Variado, Victor Miguel Ponce, San Diego State University, 2014; Traduzido por Vassiliki Boulomytis, Instituto Federal de Educação, Ciência e Tecnologia de São Paulo

[Equações Governantes]   [Solução Linear]   [Ondas Cinemáticas]   [Ondas Difusivas]   [Método de Muskingum]   [Método de Muskingum-Cunge]   [Ondas Dinâmicas]   [Questões]   [Problemas]   [Referências]   •

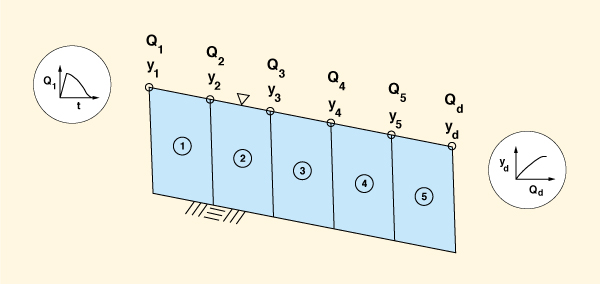
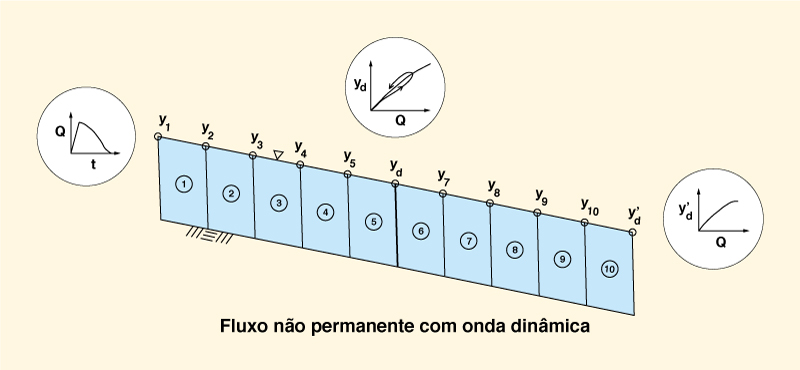
CAPÍTULO 10:
ESCOAMENTO INSTÁVEL GRADUALMENTE VARIADO

10.1 EQUAÇÕES GOVERNANTES

[Solução Linear]   [Ondas Cinemáticas]   [Ondas Difusivas]   [Método de Muskingum]   [Método de Muskingum-Cunge]   [Ondas Dinâmicas]   [Questões]   [Problemas]   [Referências]   •   [Topo]

Três princípios de conservação são aplicáveis no escoamento de canais:

Conservação da massa, que pode ser: (a) estável ou (b) instável,
Conservação de energia, que é constante (lembre-se de que a energia é igual à integral de todas as forças, excluindo a inércia, no espaço, Eq. 2-15), e
Conservação do momento instável (lembre-se de que o momento é igual à integral de todas as forças, incluindo a inércia, no tempo, Eq. 2-27).

O fluxo gradualmente variado estável combina as condições de conservação constante da massa e conservação de energia (Capítulo 7). O fluxo gradualmente variado instável combina as condições de conservação instável da massa e conservação do momento (Tabela 10-1). Assim, o fluxo gradualmente variado instável difere do fluxo gradualmente variado estável em sua descrição da variação temporal das variáveis de fluxo (vazão, estágio, profundidade do fluxo, velocidade média e assim por diante).
Na prática, o fluxo gradualmente variado estável é simplesmente chamado de "fluxo gradualmente variado" (FGV), enquanto o fluxo gradualmente variado instável é geralmente chamado de "fluxo instável" (FI).

Tabela 10-1 Leis da conservação e tipos de fluxo gradualmente variado.

Modelo Primeira equação:
Conservação de massa, para um ou outro → Massa estável Massa instável

Segunda equação:
Conservação de → Energia Momento

Flow Tipo (nome) → Estável (FGV) Instável (FI)

Geralmente tratado como sendo → Fluxo variado gradualmente Fluxo instável

Tratado em → Capítulo 7 Capítulo 10
(atual)

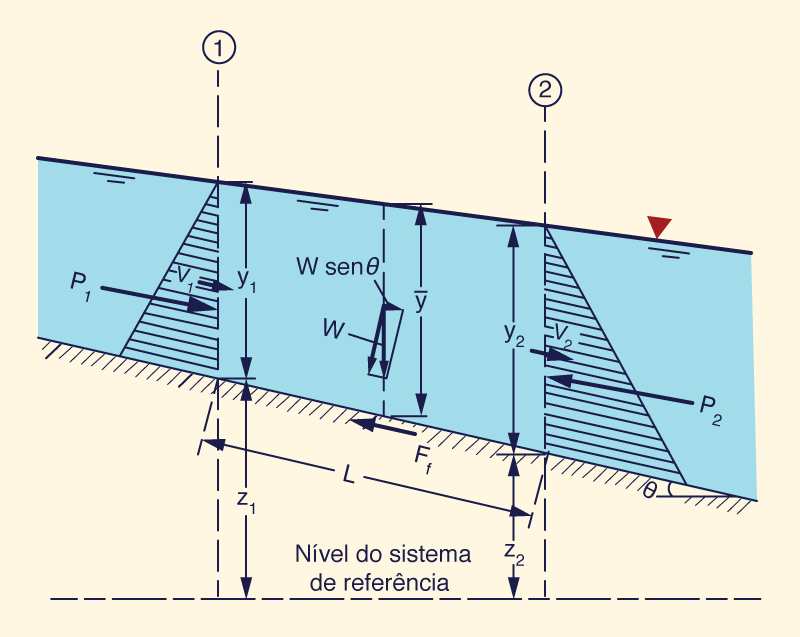
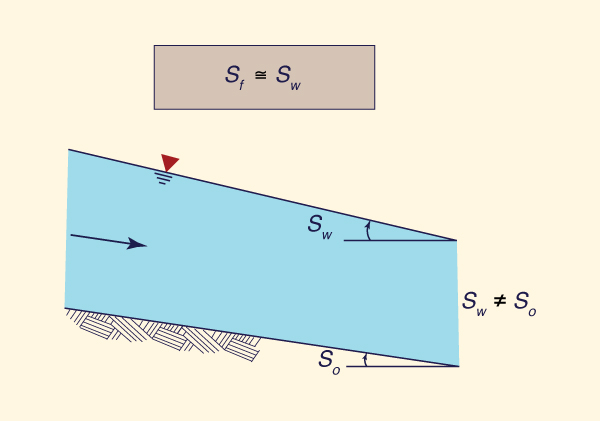
A Fig. 10-1 mostra as forças que atuam em um volume de controle. Uma força corporal e duas forças superficiais são mostradas. A força do corpo é o componente da força gravitacional resolvida ao longo da direção do movimento (W sin θ). As forças da superfície são: (1) a força devida ao gradiente de pressão (devido à diferença nas profundidades do fluxo), P₂ - P₁ e (2) a força desenvolvida ao longo do limite inferior devido ao atrito (F_f). Quando essas três forças estão em equilíbrio ao longo da direção do movimento, o fluxo é constante no ponto de vista da força. Quando as três forças NÃO estão em equilíbrio ao longo da direção do movimento, o fluxo é instável e uma quarta força surge (a força da inércia) para produzir um equilíbrio.

Forças do corpo e da superfície em um volume de controle

Fig. 10-1 Forças do corpo e da superfície em um volume de controle.

Equações principais
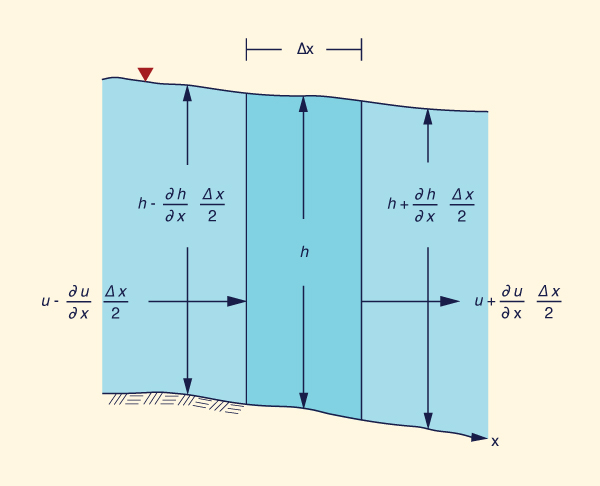
A derivação das equações principais do fluxo instável (Fig. 10-2), também denominado de fluxo variado gradualmente instável ou das equações de águas rasas (Liggett, 1975), considera as declarações de conservação de massa e momento em um volume de controle (Fig. 10-3).

Desenho esquemático para a profundidade h e velocidade do escoamento u sob o fluxo instável

Fig. 10-2 Desenho esquemático para a profundidade h e velocidade do escoamento u
sob o fluxo instável.

Gradientes de escoamento de profundidade e velocidade em um volume de controle

Fig. 10-3 Gradientes de escoamento de profundidade e velocidade em um volume de controle.

A declaração de conservação de massa é:

Entrada - saída = alteração no armazenamento

Para um canal de largura unitária (Liggett, 1975):

          ∂u   Δx              ∂h    Δx                    ∂u   Δx              ∂h    Δx            ∂h
(u - ^____ ^____ ) (h - ^____ ^____ ) - (u + ^____ ^____ ) (h + ^____ ^____ ) = ^____ Δx
          ∂x     2               ∂x     2                     ∂x    2                ∂x      2             ∂t
(10-1)

Simplificando e ignorando os termos de segunda ordem como Δx → 0:

  ∂h            ∂h           ∂u
^____ + u ^____ + h ^____ = 0
  ∂t             ∂x           ∂x
(10-2)

  ∂h         ∂
^____ + ^____ (uh) = 0
  ∂t         ∂x
(10-3)

A equação 10-3 é a equação de conservação instável da massa, geralmente chamada de equação de continuidade. No entanto, seu nome completo é: a equação diferencial de continuidade da água.
Para fluxo estável: ∂h/∂t = 0 e Eq. 10-3 reduz para: q = uh = constante. Em geral, para um canal da área de fluxo A, a equação de continuidade da água constante é: Q = uA = constante.
A declaração da conservação do momento é:

A taxa líquida de momento que entra no volume de controle + a soma das forças que atuam sobre ele = a taxa de acumulação de momento.

O momento, por unidade de largura do canal, é: ρ u (uh). Portanto, a taxa líquida de momento que entra no volume de controle F_Δ (força por unidade de largura) é:

                                   ∂                    Δx                                  ∂                     Δx
F_Δ = ρ { u (u h) - ^____ [ u (u h) ] ^____ } - ρ { u (u h) + ^____ [ u (u h) ] ^____ }
                                 ∂x                      2                                  ∂x                     2

(10-4)

As forças que atuam no volume de controle, resolvidas ao longo da direção do movimento, são: (1) força gravitacional, (2) força do gradiente de pressão e (3) força de atrito (Fig. 10-1).
A força gravitacional, por unidade de largura, é:


F_g = ρ g h Δx sin θ ≅ ρ g h Δx tan θ = ρ g h Δx S_o
          (10-5)

A força do gradiente de pressão, por unidade de largura, desenvolvida ao longo dos lados do volume de controle, é:

           h                       h                             1
F_p = ∫ p dz = ρ g ∫ (h - z ) dz = = ^____ ρ g h²
          0                       0                              2
(10-6)

A força de atrito, por unidade de largura, desenvolvida ao longo do fundo do canal, se assemelha à força gravitacional, mas é oposta ao sinal:


F_f = - ρ g h Δx S_f
          (10-7)

Em que: S_f = declividade do atrito. [Como exceção dos canais de declive adverso do fundo, para os quais S_o < 0, as forças gravitacionais e de atrito são do mesmo sinal].
O tamanho do volume de controle, por unidade de largura, é: (h Δx). A massa, por unidade de largura, é: (ρ h Δx). O momento, por unidade de largura, é: (ρ u h Δx). Assim, o fluxo de momento, ou seja, a taxa de acumulação do momento F_m, por unidade de largura, é:
             ∂
F_m = ^____ (ρ u h) Δx
            ∂t
(10-8)

A conservação do momento é:


F_Δ + F_g + F_p + F_f = F_m
          (10-9)

Substituindo as Eqs. 10-4 a 10-8 na Eq. 10-9:
                         ∂                Δx                                   ∂                 Δx
ρ { (u² h ) - ^____ (u² h ) ^____ } - ρ { (u² h ) + ^____ (u² h ) ^____ }   +   ρ g h Δx S_o
                        ∂x                 2                                   ∂x                 2

        1                        ∂h²   Δx                     ∂h²    Δx
+ ^____ ρ g [ (h² - ^_____ ^____ ) - (h² + ^_____ ^____ ) ]   +   ρ g h Δx S_f
        2                         ∂x      2                       ∂x       2

         ∂
  =   ^____ (ρ u h) Δx
        ∂t

(10-10)

Simplificando a Eq. 10-10:

  ∂                     ∂                      g     ∂h²
^____ (u h ) + ^____ (u² h ) + ^____ ^______   =   g h (S_o - S_f )
  ∂t                   ∂x                     2      ∂x

(10-11)

A equação 10-11 está em forma de conservação. Para certas aplicações, ele deve permanecer nesse forma. No entanto, muitas vezes é expresso de forma reduzida, operando com derivativos:
    ∂u            ∂h             ∂                             ∂u               ∂h
h ^____ + u ^____ + u ^____ (u h ) + (u h ) ^____ + g h ^____   =   g h (S_o - S_f )
    ∂t             ∂t             ∂x                            ∂x                ∂x
(10-12)

O segundo e o terceiro termo da Eq. 10-12 implicam nelas a equação de continuidade (Eq. 10-3). Assim, a Eq. 10-12 se reduz para:
  ∂u            ∂u             ∂h
^____ + u ^____ + g ^____ + g (S_f - S_o ) = 0
  ∂t             ∂x             ∂x
(10-13)

Dividindo por g, a Eq. 10-13 é expressa em unidades de declividade:
  1       ∂u           u      ∂u            ∂h
^____ ^_____ + ^____ ^_____ + ^_____ + (S_f - S_o ) = 0
  g       ∂t            g      ∂x            ∂x

(10-14)

A equação 10-14 é chamada de equação do movimento. É expressa em termos de declividades da seguinte maneira:

S_a + S_c + S_p + S_f - S_o = 0

(10-15)

Em que : S_a = declividade da aceleração local;
                S_c = declividade de aceleração convectiva;
                S_p = declividade de gradiente de pressão;
                S_f = declividade de atrito;
                S_o = declividade de fundo.
Tipos de onda
A equação 10-15 indica que o balanço do momento é essencialmente um balanço de declividades. No caso geral, quando todas as forças estão presentes, todas as declividades estão atuando e a solução é a mais geral. Em certos casos, no entanto, uma ou mais declividades podem ser reduzidas a zero ou consideradas desprezíveis (em comparação com as demais declividades). Essa simplificação dá origem a vários tipos de ondas, descritos na Tabela 10-2.

Table 10-2 Tipos de ondas em canais de escoamento instável.

No. Tipo de onda Declividade Nome usual Aplicações

S_a S_c S_p S_f S_o

1 Onda cinemática ✓ ✓ Onda cinemática Fluxo de transbordamento

2 Onda cinemática com difusão ✓ ✓ ✓ Onda de difusão Rota de inundação

3 Onda dinâmica ✓ ✓ ✓ Onda de
gravidade Calhas de laboratório,
pequenos canais

4 Onda dinâmica estável ✓ ✓ ✓ ✓ Onda dinâmica estável Casos especiais

5 Onda dinâmica-cinemática mista ✓ ✓ ✓ ✓ ✓ Onda dinâmica Rota de inundação em ruptura de barragem

Aplicabilidade dos tipos de onda
Ondas cinemáticas [1] aplicam-se em fluxos de transbordamento, quando as declividades do fundo são íngremes, geralmente maiores que S_o > 0,01.
Ondas de difusão [2] aplicam-se em propagação de inundações em córregos e rios, com declividades intermediárias (0,01 > S_o > 0,0001).
Ondas dinâmicas [3] aplicam-se às ondas curtas de calhas de laboratório e pequenos canais.
Ondas dinâmicas estáveis [4] aplicam-se em alguns casos especiais quando o termo da aceleração (S_a) pode ser desprezado na prática. Em geral, 5 é mais preciso desprezar both S_a e S_c (ou seja, a onda de difusão[2]) do que apenas S_a (Ponce, 1990).
Ondas cinemáticas-dinâmicas mistas [5] aplicam-se a uma onda repentina, como a que se origina em uma ruptura de barragem, e também podem se aplicar a canais com declividade muito suave (S_o < 0.0001). Observe que, na prática, existe uma confusão no uso do termo "onda dinâmica" para as ondas que incluem ambos os termos de inércia (S_a e S_c), ou seja, tipos de ondas [3] e [5].

10.2 SOLUÇÃO LINEAR

[Ondas Cinemáticas]   [Ondas Difusivas]   [Método de Muskingum]   [Método de Muskingum-Cunge]   [Ondas Dinâmicas]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Equações Governantes]

As equações 10-2 e 10-14 são as que governam a continuidade e o movimento, também conhecidas como equações de Saint-Venant (Saint-Venant, 1871). Elas são repetidas aqui por conveniência, como sendo as Eqs. 10-16 e 10-17, respectivamente.

  ∂h            ∂h           ∂u
^____ + u ^____ + h ^____ = 0
  ∂t             ∂x           ∂x
(10-16)

  1       ∂u           u      ∂u            ∂h
^____ ^_____ + ^____ ^_____ + ^_____ + (S_f - S_o ) = 0
  g       ∂t            g      ∂x            ∂x

(10-17)

Essas equações constituem um conjunto de duas equações diferenciais parciais não lineares (na verdade, quase-lineares), que quando combinadas adequadamente, resultam em uma equação diferencial parcial de segunda ordem do tipo hiperbólico, apresentando duas soluções. Até esta data, não há solução analítica de forma fechada do conjunto de Eqs. 10-16 e 10-17. Uma solução aproximada pode ser obtida linearizando o conjunto de equações e usando as ferramentas de análise de estabilidade linear (Ponce e Simons, 1977).
A inclinação de atrito S_f está diretamente relacionada à tensão de cisalhamento inferior τ pela expressão (semelhante à Eq. 6-16):

            τ
S_f = ^_____
           γ h
(10-18)

De modo usual nos cálculos de estabilidade, as Eqs. 10-16 e 10-17 devem satisfazer o fluxo não perturbado, para o qual u = u_o , h = h_o , e τ = τ_o. Eles também devem satisfazer o fluxo perturbado, para o qual u = u_o + u' , h = h_o + h' , e τ = τ_o + τ'. O sobrescrito ' representa uma pequena perturbação no fluxo uniforme e constante. Assim, todos os termos quadráticos nos componentes flutuantes podem ser negligenciados devido a um raciocínio de ordem de magnitude.
Substituindo as variáveis de perturbação nas Eqs. 10-16, 10-17 e 10-18, ocorre a linearização (Lighthill e Whitham, 1955):

  ∂h'            ∂h'             ∂u'
^____ + u_o ^____ + h_o ^____ = 0
  ∂t              ∂x             ∂x
(10-19)

  1       ∂u'          u_o     ∂u'           ∂h'                  τ'           h'
^____ ^_____ + ^____ ^_____ + ^_____ + S_o ( ^_____ - ^_____ ) = 0
  g       ∂t            g      ∂x            ∂x                  τ_o          h_o

(10-20)

Em que:

            τ_o
S_o = ^_____
           γ h_o
(10-21)

A tensão de cisalhamento limite τ pode estar relacionada à velocidade média u da seguinte maneira (Eq. 5-3):

τ = f ρ u²

(10-22)

Em que, o fator de atrito f é (Eq. 5-12):

           g
f = ^______
          C²
(10-23)

Tendo em vista a Eq. 10-22, a Eq. 10-20 é convertida em:

  1       ∂u'          u_o     ∂u'           ∂h'                         u'           h'
^____ ^_____ + ^____ ^_____ + ^_____ + - S_o ( 2 ^_____ - ^_____ ) = 0
  g       ∂t            g      ∂x            ∂x                         u_o           h_o

(10-24)
Análise de pequenas perturbações
A solução para uma pequena perturbação na profundidade do fluxo é postulada da seguinte forma exponencial (Ponce e Simons, 1977):

  h'
^____ = h_{_*} e ^{i (σ_{_*} x_{_*} - β_{_*} t_{_*} )}
h_o
(10-25)

Em que: o subscrito _{_*} indica as variáveis adimensionais;
                i = (-1)^1/2;
                σ_{_*} = número de onda adimensional;
                β_{_*} = fator de propagação complexo adimensional;
                x_{_*} e t_{_*} = coordenadas espaciais e temporais adimensionais.
Assim sendo:

             2 π
σ_{_*} = ( ^_____ ) L_o
              L

(10-26)

               2 π       L_o
β_{_R}_{_*} = ( ^_____ ) ^_____
                T         u_o

(10-27)

            x
x_{_*} = ^_____
           L_o

(10-28)

              u_o
t_{_*} = t ^_____
             L_o

(10-29)

Em que: β_{_I}_{_*} = factor de propagação de amplitude;
                L_o = comprimento do canal.
No canal, o fluxo uniforme apresenta queda de carga igual à sua profundidade:
            h_o
L_o = ^_____
           S_o

(10-30)

O distúrbio de profundidade está associado a um distúrbio de velocidade da forma:
  u'
^____ = u_{_*} e ^{i (σ_{_*} x_{_*} - β_{_*} t_{_*} )}
u_o
(10-31)

A substituição das Eqs. 10-25 e 10-31 nas Eqs. 10-19 e 10-24 produz o conjunto:

σ_{_*} u_{_*} + (σ_{_*} - β_{_*} ) d_{_*} = 0
(10-32)


[ 2 + i F_o² (σ_{_*} - β_{_*} ) ] u_{_*} + (i σ_{_*} - 1 ) d_{_*} = 0

(10-33)

No qual:
        u_o²
F_o² = ^______
              g h_o
(10-34)

As equações 10-32 e 10-33 constituem um sistema homogêneo de equações lineares nas incógnitas u_{_*} e h_{_*}. Para que a solução não seja trivial, o determinante da matriz do coeficiente deve desaparecer. Portanto, a seguinte relação é válida:

i β_{_*}² F_o² - i σ_{_*}² (1 - F_o² ) + 3 σ_{_*} - 2 β_{_*} - 2 i σ_{_*} β_{_*} F_o² = 0

(10-35)

A equação 10-35 é a equação característica que governa a propagação de ondas de águas rasas de pequena amplitude . Através da manipulação algébrica, a Eq. 10-35 é reduzida para:

F_o² β_{_*}² - 2 (σ_{_*} F_o² - i ) β_{_*} - [ σ_{_*}² (1 - F_o² ) + 3 σ_{_*} i ] = 0

(10-36)

A solução da Eq. 10-36 é (Ponce e Simons, 1977):
                                                1
β_{_*} = σ_{_*} ( 1 - i ζ ) + σ_{_*} [ ( ^______ - ζ² ) + i ζ ] ^1/2
                                              F_o²

(10-37)

No qual:
              1
ζ = ^_________
          σ_{_*} F_o²

(10-38)

As equações para celeridade adimensional e atenuação para as ondas primárias e secundárias são:
                       C + A
c₁_{_*} = 1 + ( ^_________ )^1/2
                            2

(10-39)

                        B - E
δ₁ = - 2π ^{_____________}
                     | 1 + D |

(10-40)

                       C + A
c₂_{_*} = 1 - ( ^_________ )^1/2
                           2

(10-41)

                        B + E
δ₂ = - 2π ^{_____________}
                     | 1 - D |

(10-42)

No qual:
            1
A = ^______ - ζ²
          F_o²

(10-43)


B = ζ

(10-44)

                 1
C = [ ( ^______ - ζ² ) ² + ζ² ] ^1/2
               F_o²

(10-45)

             C + A
D = ( ^_________ )^1/2
                 2

(10-46)

             C - A
E = ( ^_________ )^1/2
                 2

(10-47)

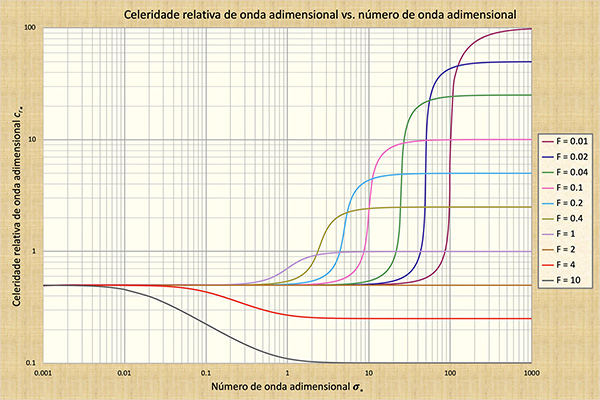
A celeridade relativa da onda sem dimensão é:
               C + A
c_r_{_*} = ( ^_________ )^1/2 = D
                   2

(10-48)

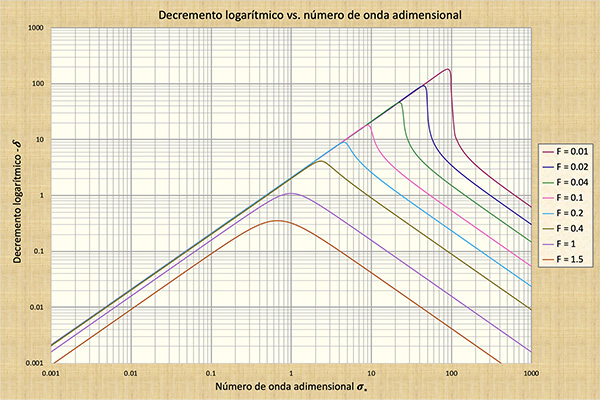
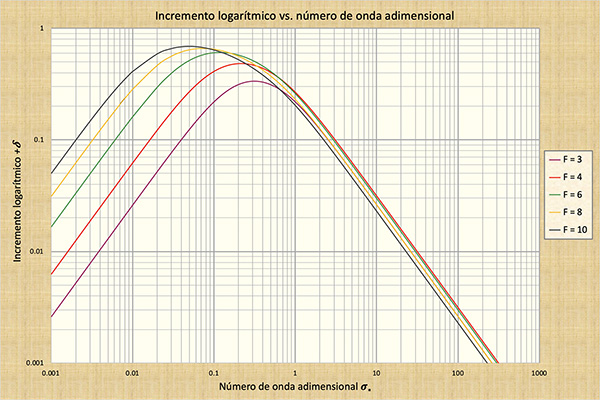
A Fig. 10-4 mostra um gráfico da velocidade relativa sem dimensão da onda c_r_{_*} versus o número de onda adimensional σ_{_*}. A Fig. 10-5 mostra um gráfico do decremento logarítmico da onda primária -δ₁ versus o número de onda adimensional σ_{_*}, aplicável aos números de Froude F < 2. A Fig. 10-6 mostra um gráfico do incremento logarítmico da onda primária +δ₁ versus o adimensional número de onda σ_{_*}, aplicável aos números de Froude F < 2. Com base nessas figuras, as características das ondas rasas serão descritas no quadro a seguir.

Celeridade da onda relativa adimensional versus o número de onda adimensional em um fluxo do canal instável

Fig. 10-4 Celeridade da onda relativa adimensional versus o número de onda adimensional em um fluxo do canal instável.

Decremento logarítmico da onda primária para os números de Froude F < 2

Fig. 10-5 Decremento logarítmico da onda primária para os números de Froude F < 2.

Incremento logarítmico da onda primária para os números de Froude F > 2

Fig. 10-6 Incremento logarítmico da onda primária para os números de Froude F > 2.

Propagação de ondas rasas em fluxo de canais ¹

As ondas cinemáticas situam-se na extrema esquerda do espectro de número de onda, com celeridade relativa adimensional c_r_{_*} (sob atrito Chezy) e têm muito pouca ou nenhuma atenuação sob F < 2 (decréscimo logarítmico muito pequeno).
As ondas de difusão estão à esquerda do espectro do número de onda, com celeridade relativa sem dimensão aproximadamente igual a c_r_{_*} (sob atrito Chezy) e atenuação pequena, mas mensurável, sob F < 2 (pequeno decréscimo logarítmico).
As ondas dinâmicas estão à extrema direita do espectro de número de onda, com celeridade relativa adimensional c_r_{_*} = 1/F e muito pouca, se houver atenuação sob F < 2 (decréscimo logarítmico muito pequeno).
Ondas cinemáticas-dinâmicas mistas estão localizadas no meio do espectro de número de onda, com variação da celeridade relativa sem dimensão e atenuação muito forte sob F < 2 (grande decréscimo logarítmico).
Para o número Vedernikov V < 1, que corresponde a F < 2 (atrito de Chezy em canais hidraulicamente amplos), a celeridade relativa sem dimensão varia amplamente em todo o espectro do número de onda. A atenuação máxima ocorre no ponto de inflexão da curva de celeridade adimensional.
Para V = 1, que corresponde a F = 2, a celeridade relativa adimensional é uma constante em todo o espectro de número de onda. Essa condição de fluxo é o limiar para o desenvolvimento de ondas de rolagem, que ocorrem para F ≥ 2 ( Craya, 1952 ).
Para V > 1, que corresponde a F > 2, a celeridade relativa sem dimensão varia ao longo do espectro do número de onda. A amplificação máxima (ou seja, atenuação negativa) ocorre no ponto de inflexão da curva de celeridade adimensional.

¹ Ver Ponce e Simons (1977) para um tratamento detalhado da propagação de ondas rasas no fluxo de canal aberto.

10.3 ONDAS CINEMÁTICAS

[Ondas Difusivas]   [Método de Muskingum]   [Método de Muskingum-Cunge]   [Ondas Dinâmicas]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Equações Governantes]   [Solução Linear]

Uma onda cinemática é uma idealização (de fluxo instável de canal aberto gradualmente variado) que negligencia os termos de aceleração (local e convectivo) e o termo de gradiente de pressão (Tabela 10-2). Negligenciando estes termos, a equação de movimento (Eq. 10-14) é reduzida a uma declaração de fluxo uniforme e constante:


S_f = S_o

(10-49)

A instabilidade do fenômeno, no entanto, é preservada através do termo variável no tempo na equação de continuidade (Eq. 10-3). A combinação das equações Eqs. 10-3 e 10-49 dão origem à equação da onda cinemática.
A partir de q = uh, a Eq. 10-3 pode ser expressa em termos de descarga na largura da unidade:

  ∂h        ∂q
^____ + ^____ = 0
  ∂t         ∂x
(10-50)

Em termos de descarga Q, a equação de continuidade é:

  ∂A         ∂Q
^_____ + ^_____ = 0
   ∂t          ∂x
(10-51)

Uma declaração de fluxo uniforme (Eq. 10-49) pode ser adequadamente representada pela classificação da área de descarga:


Q = α A^β

(10-52)

Em que: α e β são coeficientes e expoentes, respectivamente.
O coeficiente β varia em função do tipo de atrito, da forma da seção transversal e da inclinação do fundo. O expoente β varia em função do tipo de atrito e da forma da seção transversal.
Assumindo, por uma questão de simplicidade, que α e β são independentes de A, a partir da Eq. 10-52 tem-se que:

  dQ
^_____ = α β A ^{β - 1}
  dA
(10-53)

  dQ             Q
^_____ = β ^____
  dA              A
(10-54)

  dQ
^_____ = β V
  dA
(10-55)

Em que: V = Q / A = velocidade média.
A equação da onda cinemática é obtida combinando as Eqs. 10-51 e 10-55 para produzir:

  ∂Q                 ∂Q
^_____ + β V ^_____ = 0
   ∂t                  ∂x
(10-56)

Em termos de descarga por largura da unidade q:

   ∂q                 ∂q
^_____ + β V ^_____ = 0
   ∂t                  ∂x
(10-57)

Celeridade convectiva
A equação 10-56 (ou Eq. 10-57) é uma equação diferencial parcial de primeira ordem. Descreve a convecção da quantidade Q (ou q) com a velocidade convectiva ou celeridade c_k, que corresponde a:


c_k = β V
                (10-58)

Dada a Eq. 10-55, a velocidade convectiva também pode ser expressa como:

           dQ
c_k = ^_____
           dA
(10-59)

Dado que dA = T dy (Eq. 3-11), onde T = largura superior do canal e y = estágio, a velocidade convectiva também pode ser expressa da seguinte forma:

            1      dQ
c_k = ^____ ^_____
           T       dy              (10-60)

A equação 10-60 foi originalmente derivada de Kleitz (1877) e mais tarde foi descoberta a partir de observações reais de campo por Seddon (1900). É frequentemente referida como Lei de Kleitz-Seddon, ou simplesmente Lei de Seddon. A equação 10-58 é usada quando β é conhecido. Já a Eq. 10-59 é usada em formulações teóricas, e a Eq. 10-60 em aplicações práticas.
Já que a Eq. 10-56 é uma equação diferencial parcial de primeira ordem, ela não permite a difusão das ondas (atenuação ou dissipação das ondas). A difusão só pode ser obtida através de um termo de segunda ordem. Sob a suposição de linearidade (celeridade convectiva constante), uma onda cinemática tornará a sua vazão convectiva e sem difusão de onda; isto é, a vazão manterá a sua forma e permanecerá constante no espaço e no tempo após a propagação.

Ausência de difusão de ondas cinemáticas

A ausência de difusão de ondas pode ser demonstrada ainda mais por um argumento matemático. A derivada total para Q é:

            ∂Q              ∂Q
dQ = ^_____ dt + ^_____ dx
            ∂t                ∂x (10-61)

Assim sendo:

  dQ          ∂Q           dx      ∂Q
^_____ = ^_____ + ^_____ ^_____
  dt            ∂t             dt       ∂x (10-62)

Como já visto antes, a equação da onda cinemática é:

  ∂Q                 ∂Q
^_____ + β V ^_____ = 0
   ∂t                  ∂x (10-56)

Comparando a Eq. 10-62 com a Eq. 10-56, segue que dQ/dt, isto é, Q permanece constante ao lonmgo do tempo para as ondas que viajam com a celeridade convectiva β V.

Choque cinemático
Quando a suposição de linearidade é relaxada, a onda cinemática pode mudar de forma tornando-se (a) mais íngreme [Fig. 10-7 (a)] ou (b) mais plana [Fig. 10-7 (b)]. O fato de uma onda ficar inclinada ou achatada dependerá em grande parte da forma da seção transversal do canal. Dois limites assintóticos são reconhecidos: (1) ondas que se propagam em canais hidraulicamente amplos, enquanto (2) ondas que se propagam em canais inerentemente estáveis (Capítulo 1). Nos canais hidraulicamente amplos, as ondas se inclinam, enquanto nos canais inerentemente estáveis, elas se achatam (Ponce e Windingland, 1985).

Inclinação da onda cinemática

Fig. 10-7 (a) Inclinação da onda cinemática.

Achatamento da onda cinemática

Fig. 10-7 (b) Achatamento da onda cinemática.

Quando permitida a continuidade sem ser monitorada, a inclinação resulta em uma onda cinemática que se torna um choque cinemático . Assim, um choque cinemático é um recurso instável de fluxo de canal aberto intrinsecamente relacionado à onda cinemática: uma onda deve ser cinemática antes que possa se transformar em um choque cinemático (Lighthill e Whitham, 1955). Kibler e Woolhiser (1970) procuraram esclarecer a ocorrência de fenômenos de choque cinemático, afirmando:

"Embora o desenvolvimento das ondas de choque possa surgir sob certas circunstâncias físicas altamente seletivas, é considerado neste estudo como uma propriedade das equações matemáticas usadas para explorar o problema do fluxo terrestre, em vez de uma característica observável desse processo hidrodinâmico ..."

Assim, o choque cinemático é real, mas raro, no mundo físico, onde as irregularidades espaciais se manifestam como difusão, com o efeito líquido de impedir o desenvolvimento do choque. Por outro lado, é provável que o mundo computacional seja muito mais regular, inibindo assim a difusão e promovendo o desenvolvimento de choque "numérico".
Celeridade das ondas cinemáticas
A celeridade relativa da onda cinemática, ou seja, a celeridade da onda cinemática tomada em relação à velocidade do fluxo, é:


c_rk = (β - 1 ) V
                (10-63)

Além disso, a celeridade relativa da onda cinemática sem dimensão é:

              c_rk
c_drk = ^_____ = β - 1
              V
(10-64)

De acordo com a Eq. 1-11, a celeridade relativa da onda cinemática adimensional é:

                           V
c_drk = β - 1 = ^____
                           F (10-65)

Assim, para V = 1, ou seja, para um fluxo neutro e estável, o número de Froude é:

                1               1
F_ns = ^_______ = ^_______
              β - 1          c_drk
(10-66)

A Table 10-3 mostra a variação de: (a) o expoente β, (b) a celeridade relativa da onda cinemática adimensional c_drk e (c) o número de Froude com estabilidade neutra, com tipos selecionados de atrito e formato da seção transversal.

Table 10-3 Variação de β em função do tipo de atrito e da forma da seção transversal.

[1] [2] [3] [4] [5] [6]

β 24 β Tipo de atrito Forma da seção transversal c_drk F_ns

3 72 Laminar Hidraulicamente larga 2 1/2

8/3 64 Laminar-turbulento misto
(Manning 25% turbulento) Hidraulicamente larga 5/3 3/5

21/8 63 Laminar-turbulento misto
(Chezy 25% turbulento) Hidraulicamente larga 13/8 8/13

7/3 56 Laminar-turbulento misto
(Manning 50% turbulento) Hidraulicamente larga 4/3 3/4

9/4 54 Laminar-turbulento misto
(Chezy 50% turbulento) Hidraulicamente larga 5/4 4/5

2 48 Laminar-turbulento misto
(Manning 75% turbulento) Hidraulicamente larga 1 1

15/8 45 Laminar-turbulento misto
(Chezy 75% turbulento) Hidraulicamente larga 7/8 8/7

5/3 40 Manning turbulento Hidraulicamente larga 2/3 3/2

3/2 36 Chezy turbulento Hidraulicamente larga 1/2 2

4/3 32 Manning turbulento Triangular 1/3 3

5/4 30 Chezy turbulento Triangular 1/4 4

1 24 Qualquer Inerentemente estável 0 ∞

As seguintes conclusões podem ser obtidas a partir da Table 10-3:

O valor do expoente nominal varia de tão alto quanto β = 3 para o fluxo laminar em um canal hidraulicamente amplo, e tão baixo quanto β = 1 = 1 para um canal inerentemente estável.
O valor da celeridade relativa das ondas cinemáticas relativas adimensionais varia de tão alto quanto c_drk = 2 para o fluxo laminar em um canal hidraulicamente amplo, e tão baixo quanto c_drk = 0 para um canal inerentemente estável.
O número de Froude para estabilidade neutra varia entre tão baixo quanto F_ns = 0,5 para o fluxo laminar numa hidraulicamente canal de largura (isto é, laminar terrestre de fluxo), a tão elevado como F_ns = ∞ para um canal inerentemente estável sob qualquer tipo de atrito (embora geralmente turbulento).
A celeridade relativa das ondas cinemáticas relativas e sem dimensão do Chezy turbulenta, hidraulicamente ampla, é c_drk = 0,5, confirmando os resultados mostrados na (Fig. 10-5). Assim, as ondas cinemáticas apresentam comprimentos de onda longos L e correspondentemente "curtos" números de onda adimensionais σ_{_*}.
A celeridade relativa das ondas cinemáticas relativas adimensionais, hidraulicamente larga e Manning turbulento é c_drk = 2/3, = 2/3, ou seja, o valor de Manning excede o valor de Chezy em 1/6.

Observe que o valor de β pode ser menor que 1 para casos diferentes dos mostrados na Tabela 10-3; por exemplo, quando a seção transversal não cresce monotonicamente com o estágio, como no fluxo circular do bueiro. Além disso, observe que, como o número de Froude possui um limite superior (correspondente a um limite inferior realisticamente alcançável no atrito do fundo), o valor F_ns = ∞ tem um valor prático limitado. Se o número máximo de Froude atingível é conservadoramente F_max = 25 (Chow, 1959), o formato da seção transversal pode ser projetado de acordo, garantindo estabilidade (Ponce e Porras, 1995).
Em resumo, as ondas cinemáticas têm as seguintes propriedades:

As ondas cinemáticas viajam com celeridade relativa adimensional igual a 0,5, sob atrito de Chezy; e sob o atrito de Manning, o valor é de 2/3.
As ondas cinemáticas não atenuam, mas podem sofrer alterações de forma, devido a não linearidade; em casos extremos, em canais hidraulicamente largos, a onda cinemática pode ficar mais acentuada ao ponto em que se torna um choque cinemático.

Um pouco de cautela em relação à modelagem de ondas cinemáticas ¹

Apesar da atenuação das ondas ser negada pela teoria das ondas cinemáticas, certas soluções numéricas da Eq. 10-56 exibem uma atenuação distinta. Cunge (1969) traçou essa aparente contradição ao fato de que as soluções numéricas, em virtude de seu tamanho discreto de grade, introduzem um erro que se expressa como difusão numérica. À medida que a grade é refinada, o efeito numérico diminui; no entanto, uma grade numérica finita (sendo que todas as grades numéricas são finitas) sempre terá um erro residual.
O dilema é resolvido fazendo a difusão numérica simular à difusão física, se houver, do problema físico. Este procedimento está incorporado no método de propagação de inundação de Muskingum-Cunge, descrito na Seção 10.6.
¹ Veja Ponce (1991) para um tratamento detalhado do paradoxo em relação às ondas cinemáticas.

Classificação de ondas cinemáticas
As ondas cinemáticas são baseadas em uma classificação de área de descarga de valor único,segundo a Eq. 10-52. Assim, uma classificação de onda cinemática é de valor único, exibindo uma correspondência individual entre (a) vazão, e (b) área, profundidade ou estágio do fluxo. Uma classificação de ondas cinemáticas é calculada usando uma fórmula de fluxo uniforme, como Manning ou Chezy, para uma faixa de (a) profundidades de fluxo, em canais artificiais, ou (b) estágios de fluxo, em canais naturais.
Aplicação das ondas cinemáticas
Uma onda cinemática é um tipo simplificado de onda, em que três termos na equação de movimento (Tabela 10-2) foram negligenciados ou assumidos como sendo muito pequenos para ter algum significado prático. Assim, a onda cinemática não se aplica ao caso geral. Seu uso é recomendado para casos em que a instabilidade do fluxo é relativamente pequena. Na prática, uma onda cinemática será aplicada desde que a seguinte desigualdade sem dimensão seja satisfeita (Ponce, 1989; Ponce, 2014):

  t_r S_o V_o
^___________ ≥ 85
       d_o              (10-67)

Em que: t_r = tempo-de-ascensão do hidrograma;
             S_o = declive inferior;
             V_o = velocidade média de fluxo;
             d_o = profundidade de fluxo média.

10.4 ONDAS DIFUSIVAS

[Método de Muskingum]   [Método de Muskingum-Cunge]   [Ondas Dinâmicas]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Equações Governantes]   [Solução Linear]   [Ondas Cinemáticas]

Uma onda de difusão é uma idealização que negligencia ambos os termos de aceleração na equação do movimento (Tabela 10-2). Desprezando-se estes termos, a Eq. 10-14 é reduzida para a seguinte declaração:

                     ∂h
S_f = S_o - ^_____
                     ∂x
(10-68)

A instabilidade do fenômeno, no entanto, é preservada por meio do termo variável no tempo na equação de continuidade (Eq. 10-3). A combinação das Eqs. 10-3 e 10-68 dão origem à equação da onda de difusão.
A equação da onda cinemática foi derivada usando uma declaração de fluxo uniforme constante em vez da equação do movimento (Seção 10.4). Na derivação da equação da onda de difusão, uma declaração de fluxo não uniforme constante (a declividade do atrito é igual à declividade da superfície da água) é usada (Fig. 10-8). Nesse caso, a classificação da área de descarga, usando a fórmula de Manning em unidades SI (Eq. 5-17), é:

        1                           dh
Q = ^___ A R ^2/3 (S_o - ^____ ) ^1/2
        n                           dx
(10-69)

Em que o termo entre parênteses indica a inclinação da superfície da água S_w.

Difusão de uma suposta onda

Fig. 10-8 Difusão de uma suposta onda.

A diferença entre as ondas cinemáticas e de difusão está no termo gradiente de pressão (dh/dx). Quando esse termo é incluído na formulação, a equação resultante é de segunda ordem e, portanto, é capaz de simular a difusão. Lighthill e Whitham (1955) se referiram a essa situação como a "difusão de ondas cinemáticas", isto é, um tipo de onda cinemática, ainda sem inércia em sua formulação, que é capaz de se difundir.
Para derivar a equação da onda de difusão, a Eq. 10-51 é repetida aqui de uma forma ligeiramente diferente:

  ∂Q         ∂A
^_____ + ^_____ = 0
  ∂x           ∂t
(10-70)

A equação 10-69 é expressa de uma forma mais conveniente (Cunge, 1969):

                          dh
m Q ² = S_o - ^____
                          dx
(10-71)

Em que m é o inverso do quadrado do transporte de canal K (Eq. 5-34), repetido aqui por conveniência:

        1
K = ^___ A R ^2/3
        n
(5-34)

A partir de dA = T dh, na qual T = largura do topo, a Eq. 10-71 passa a ser:

   1       dA
^_____ ^______ + m Q ² - S_o = 0
   T       dx
(10-72)

As equações 10-70 e 10-72 constituem um conjunto de duas equações diferenciais parciais que descrevem ondas de difusão. Essas equações podem ser combinadas em uma equação com Q como variável dependente. No entanto, é necessário primeiro linearizar as equações em torno dos valores de fluxo de referência. Por simplicidade, é assumida uma largura do topo constante (supondo um canal largo).
A linearização das Eqs. 10-70 e 10-72 é realizada pela teoria das pequenas perturbações (Cunge, 1969). As variáveis Q, A, e m podem ser expressas em termos da soma de um valor de referência (com o subscrito o) e de uma pequena perturbação no valor de referência (com sobrescrito ' ): Q = Q_o + Q' ; A = A_o + A' ; m = m_o + m'. Substituindo-os nas Eqs. 10-70 e 10-72, desprezando perturbações ao quadrado e subtraindo o fluxo de referência, obtem-se:

∂Q'        ∂A'
^____ + ^____ = 0
∂x          ∂t

(10-73)

e
   1       ∂A'
^_____ ^______ + Q_o² m' + 2 m_o Q_o Q' = 0
   T       ∂x
(10-74)

Diferenciando a Eq. 10-73 em relação a x e Eq. 10-74 em relação a t resulta em:
  ∂²Q'         ∂²A'
^______ + ^_______ = 0
  ∂x²          ∂x ∂t

(10-75)

   1        ∂²A'                   ∂m'                        ∂Q'
^_____ ^_________ + Q_o² ^_____ + 2 m_o Q_o ^______ = 0
   T       ∂x ∂t                    ∂t                          ∂t
(10-76)

Usando a regra da cadeia e a Eq. 10-73 segue que:

  ∂m'          ∂m'       ∂A'                 ∂m'     ∂Q'
^_____ = ^_______ ^_______ = - ^______ ^______
   ∂t            ∂A'        ∂t                   ∂A'      ∂x
(10-77)

Combinando a Eq. 10-76 com a Eq. 10-77:

   1        ∂²A'                  ∂m'     ∂Q'                         ∂Q'
^_____ ^________ - Q_o² ^______ ^______ + 2 m_o Q_o ^______ = 0
   T       ∂x ∂t                  ∂A'      ∂x                           ∂t
(10-78)

Combinando as Eqs. 10-75 e 10-78 e reorganizando os termos, obtem-se:

  ∂Q'           Q_o       ∂m'     ∂Q'                  1             ∂Q'²
^______ - ^_______ ^______ ^______ = ^{_____________} ^_______
   ∂t           2 m_o      ∂A'      ∂x            2 T m_o Q_o      ∂x²
(10-79)

Por definição: mQ ² = S_f (Eq. 10-70). Portanto:

  ∂Q'          ∂Q                 Q_o
^_____ = ^_______ = - ^_______
  ∂m'          ∂m               2 m_o
(10-80)

E também

                   S_o
m_o Q_o = ^______
                   Q_o
(10-81)

Substituindo as Eqs. 10-80 e 10-81 na Eq. 10-79, usando a regra da cadeia e eliminando os sobrescritos para simplificar, é obtida a seguinte equação:

  ∂Q              ∂Q        ∂Q                 Q_o          ∂²Q
^______ + ( ^______ ) ^______ = ( ^_________ ) ^_______
   ∂t               ∂A         ∂x              2 T S_o        ∂x²
(10-82)

O lado esquerdo da Eq. 10-82 é reconhecida como a equação da onda cinemática, com ∂Q/∂A como a celeridade da onda cinemática. O lado direito é um termo de segunda ordem (diferencial parcial) que explica o efeito da difusão física. O coeficiente do termo de segunda ordem possui as unidades de difusividade [L² T ^-1],, sendo denominadas difusividade hidráulica ou difusividade do canal.

A difusividade hidráulica, uma característica do fluxo e do canal, é definida da seguinte forma:

               Q_o               q_o
ν_h = ^_________ = ^_______
            2 T S_o          2 S_o (10-83)

Em que q_o = Q_o /T é a vazão de referência por unidade de largura do canal. Da Eq. 10-83, conclui-se que a difusividade hidráulica é pequena para declividades íngremes do fundo (por exemplo, os de córregos das montanhas) e grande para declividades suaves (por exemplo, os de grandes rios próximos à foz).
A Equação 10-82 descreve o movimento das ondas de inundação de uma maneira melhor que a Eq. 10-50. Embora não consiga descrever todos os efeitos inerciais, ele fisicamente explica a atenuação das ondas.
A Equação 10-82 é uma equação diferencial parcial parabólica de segunda ordem. Pode ser resolvida analiticamente, levando à solução de analogia de difusão para ondas de inundação (Hayami, 1951), ou numericamente com o auxílio de um esquema numérico para equações parabólicas. Uma abordagem alternativa é combinar a difusividade hidráulica (Eq. 10-83) com o coeficiente de difusão numérica do método de propagação de inundação de Muskingum (Seção 10.5). Essa abordagem é a base do método Muskingum-Cunge (Seção 10.6).
Classificação de ondas de difusão
As ondas de difusão não são baseadas na classificação da área de descarga com valor único. Assim, uma classificação de onda de difusão não é de valor único, exibindo um lasso (ou loop). Em geral, no entanto, o lasso é relativamente pequeno e pode ser negligenciado por motivos práticos. Uma classificação de ondas cinemáticas pode ser usada como uma aproximação na propagação de ondas de difusão.
Celeridade das ondas de difusão
De acordo com a Eq. 10-82, a celeridade das ondas de difusão deve ser a mesma que a celeridade das ondas cinemáticas (Ponce e Simons, 1977). No entanto, as ondas de difusão atenuam; portanto, a classificação real da área de descarga não é exatamente de valor único. Na prática, a celeridade das ondas de difusão é igual à celeridade das ondas cinemáticas apenas como uma aproximação.
Aplicação das ondas de difusão
Uma onda de difusão é um tipo simplificado de onda, em que dois termos na equação de movimento (Tabela 10-2) foram negligenciados ou assumidos como sendo muito pequenos para ter algum significado prático. Assim, embora a onda de difusão se aplique a uma gama mais ampla de casos do que a onda cinemática, ela ainda não é adequada ao caso geral. Seu uso é recomendado para casos em que a instabilidade do fluxo é de tamanho pequeno a médio (onde a onda permanece dentro de 30% da sua força original, em um período de propagação). Uma onda de difusão será aplicada desde que a seguinte desigualdade adimensional seja satisfeita (Ponce, 1989; Ponce, 2014):

               g
t_r S_o ( ^____ )^1/2 ≥ 15
              d_o            (10-84)

Em que: t_r = tempo-de-ascensão do hidrograma;
              S_o = declividade inferior;
              g   = aceleração gravitacional;
              d_o = profundidade de fluxo média.

As ondas de difusão aplicam-se a problemas de propagação de ondas de inundação (veja analogia de difusão de Hayami de ondas de inundação no quadro a seguir). Enquanto as ondas cinemáticas se aplicam às ondas de inundação que não se difundem, as ondas de difusão se aplicam às ondas de inundação que atenuam significamente. Enquanto a onda de difusão não responde pela propagação da onda, somente a onda cinemático-dinâmica mista (leia-se "onda dinâmica", Tabela 10-2) é capaz de resolver o problema corretamente. Na prática, no entanto, as ondas de difusão se aplicam a uma ampla gama de problemas de propagação de inundações.

Analogia da difusão de Hayami das ondas de inundação
Em 1951, Hayami publicou um artigo intitulado "Sobre a propagação de ondas de inundação". Nele, ele argumentou que as ondas de inundação poderiam ser modeladas com uma equação de convecção-difusão semelhante à Eq. 10-82. Segundo Hayami:

Nos rios naturais, a forma dos canais, as declividades do leito, a largura, a forma da seção transversal, entre outros, são todos muito irregulares e mudam incessantemente... No entanto, o fluxo nos rios é constante e quase uniforme em termos amplos. As perturbações no fluxo causadas por essas irregularidades diminuem em poucos quilômetros e têm certas dimensões e durações limitadas. O caráter estocástico do coletivo dessas perturbações elementares causa uma mistura longitudinal em larga escala ... Introduzindo o efeito da difusão longitudinal causada pela mistura na equação de continuidade e assumindo que o fluxo médio tomado em uma faixa adequada seja estável e uniforme , a equação diferencial das ondas de inundação foi derivada. É uma equação de difusão que contém um termo de advecção.

Montante do Rio Paraguay próximo do Porto Murtinho

Fig. 10-9 Montante do Rio Paraguai próximo do Porto Murtinho, MS, Brasil, caracterizando uma onda de difusão. O nível do rio sobe durante 6 meses. A declividade inferior nesse ponto é de S_o = 0,00002.

Difusividade hidráulica dinâmica
A difusividade hidráulica (Eq. 10-83) é uma propriedade fundamental das ondas de difusão. Ele afirma que o coeficiente de difusão é diretamente proporcional à descarga da largura da unidade e inversamente proporcional à declividade do canal. Esta conclusão é aplicável às ondas de difusão, que são governadas pela equação de convecção-difusão representada pela Eq. 10-82.
Usando conceitos da teoria linear, Dooge (1973) desenvolveu uma equação de convecção-difusão usando a equação completa do movimento. A abordagem de Dooge estende o conceito de onda de difusão ao domínio das ondas dinâmicas (Tabela 10-2). Quando todos os termos são incluídos na formulação, a difusividade hidráulica é essencialmente dinâmica, expressa, para canais hidraulicamente largos, da seguinte maneira:

               q_o               F²
ν_hF = ^_______ ( 1 - ^______ )
              2 S_o              4
(10-85)

Ponce (1991) expressou a difusividade hidráulica dinâmica em termos do número de Vedernikov, da seguinte forma:

               q_o
ν_hV = ^_______ ( 1 - V² )
              2 S_o
(10-86)

A equação 10-86 é totalmente melhor que a Eq. 10-83. Elas são equivalentes apenas se V = 0, isto é, para fluxos muito pequenos de número de Froude. Para V = 1, usando a Eq. 10-86, a difusividade hidráulica desaparece, enquanto este não é o caso da Eq. 10-83, para os quais a difusividade hidráulica permanece finita.

10.5 MÉTODO DE MUSKINGUM

[Método de Muskingum-Cunge]   [Ondas Dinâmicas]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Equações Governantes]   [Solução Linear]   [Ondas Cinemáticas]   [Ondas Difusivas]

O método Muskingum de propagação de inundação foi desenvolvido em conexão com projetos de proteção contra inundações na Bacia do Rio Muskingum, Ohio (Fig. 10-10) (McCarthy, 1938). É o método mais usado de propagação de inundações, com inúmeras aplicações nos Estados Unidos e em todo o mundo.

Rio Muskingum próximo de Marietta

Fig. 10-10 Rio Muskingum próximo de Marietta, Ohio.

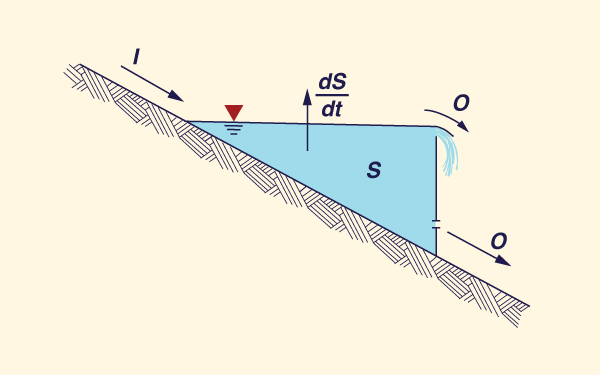
O método é baseado na equação diferencial de armazenamento (Fig. 10-11):

             dS
I - O = ^_____
             dt
(10-87)

Em que: I  = entrada;
             O = saída;
             S = armazenamento.

Definição esquemática de entrada, saída e armazenamento em um reservatório

Fig. 10-11 Definição esquemática de entrada, saída e armazenamento em um reservatório.

Em um canal ideal, o armazenamento é uma função da entrada e saída. Isso está em contraste com um reservatório ideal, no qual o armazenamento é apenas uma função da vazão. No método Muskingum, o armazenamento é uma função linear de entrada e saída:

S = K [ X I + ( 1 - X ) O ]
(10-88)

Em que: S = volume de armazenamento;
               K = constante de tempo ou coeficiente de armazenamento;
               X = um fator de ponderação adimensional.
Com entrada e saída em metros cúbicos por segundo e K em horas, o volume de armazenamento fica em (metros cúbicos por segundo)-hora. Como alternativa, K pode ser expresso em segundos, caso em que o volume de armazenamento está em metros cúbicos.
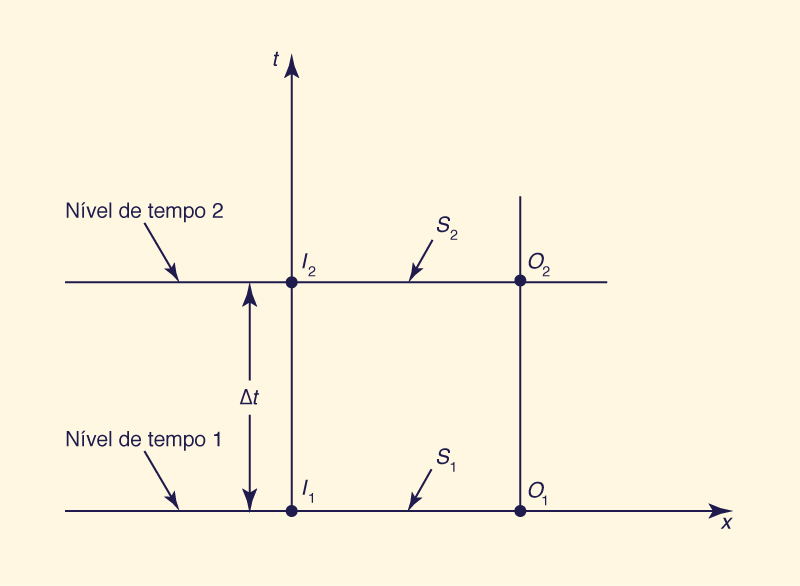
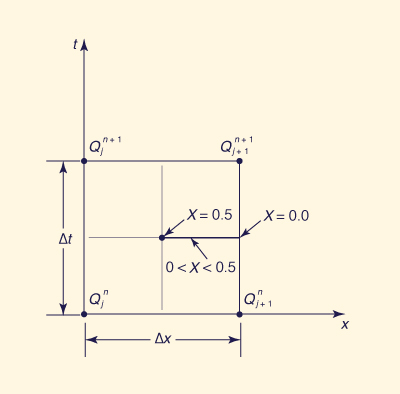
Para derivar a equação de propagação de Muskingum, a Eq. 10-87 é discretizada no plano x-t (Fig. 10-12), para produzir:

    I₁ + I₂          O₁ + O₂            S₂ - S₁
^__________ - ^___________ = ^___________
       2                    2                     Δt
(10-89)

Discretização no plano x-t

Fig. 10-12 Discretização no plano x-t.

A Eq. 10-88 é expressa nos níveis de tempo 1 e 2:

S₁ = K [ X I₁ + ( 1 - X ) O₁ ]
(10-90)

S₂ = K [ X I₂ + ( 1 - X ) O₂ ]
(10-91)

Substituindo as Eqs. 10-90 e 10-91 na Eq. 10-89, a partir da resolução de O₂ obtem-se:

O₂ = C₀ I₂ + C₁ I₁ + C₂ O₁
(10-92)

Em que C₀, C₁ e C₂ são coefficientes de propagação definidos em termos de Δt, K, e X como consta a seguir:

                ( Δt / K ) - 2X
C₀ = ^{_______________________}
            2(1 - X) + ( Δt / K )

(10-93a)

                ( Δt / K ) + 2X
C₁ = ^{_______________________}
            2(1 - X) + ( Δt / K )
(10-93b)

            2(1 - X) - ( Δt / K )
C₂ = ^{_______________________}
            2(1 - X) + ( Δt / K )
(10-93c)

Como C₀ + C₁ + C₂ = 1, os coeficientes de propagação podem ser interpretados como coeficientes de ponderação.
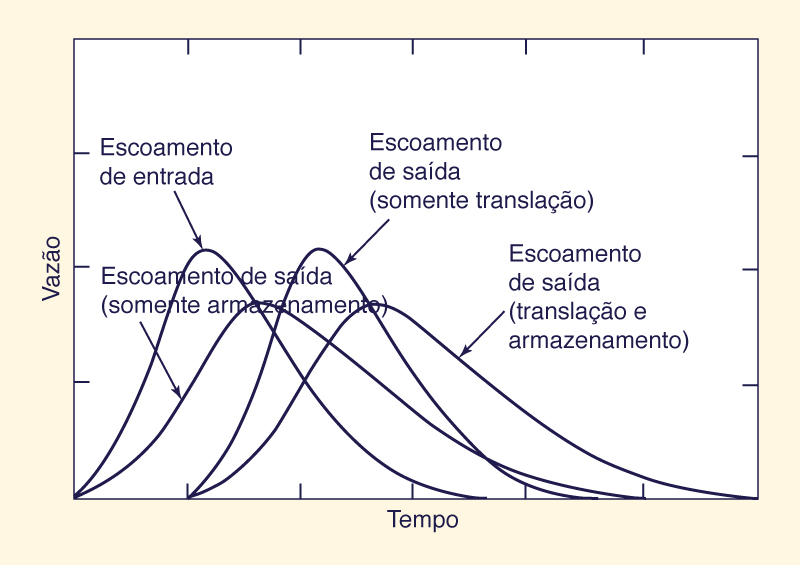
Dado um hidrograma de escoamento de entrada, uma condição de escoamento inicial, um intervalo de tempo escolhido Δt, e parâmetros de propagação X e K, os coeficientes de propagação podem ser calculados com a Eq. 10-93, e o hidrograma de saída com a Eq. 10-92. Os parâmetros de propagação X e K são relacionados às características do escoamento e do canal, sendo K interpretado como o tempo de viagem da onda de inundação da extremidade à montante até a extremidade à jusante do trecho do canal. Portanto, K é responsável pela parte da conversão do roteiro (Fig. 10-13).
O parâmetro X é responsável pela parte de armazenamento da propagação. Para um determinado evento de inundação, existe um valor de X para o qual o armazenamento no hidrograma de vazão calculado corresponde ao do hidrograma de vazão medida. O efeito do armazenamento é reduzir o pico de fluxo e espalhar o hidrograma ao longo do tempo (Fig. 10-13). Portanto, é frequentemente usado de forma intercambiável com os termos difusão e atenuação de pico.

Processos de translação e armazenagmento na propagação do curso d'água

Fig. 10-13 Processos de translação e armazenamento na propagação do curso d'água.

O parâmetro de propagação K é função do comprimento do trecho do canal e velocidade da onda de inundação. Por outro lado, o parâmetro X é função das características de fluxo e canal que causam a difusão do escoamento. No método Muskingum, X é interpretado como um fator de ponderação e restrito na faixa de 0 ≤ X ≤ 0,5. Valores de X maiores que 0,5 produzem amplificação hidrográfica (difusão negativa), que não corresponde à realidade (sob os números de Froude aplicáveis aos fluxos de inundação). Com K = Δt e X = 0,5, as condições de escoamento são tais que o hidrograma de saída mantém a mesma forma que o hidrograma do escoamento de entrada, mas é traduzido um tempo igual a jusante K. Para X = 0, o roteamento de Muskingum se reduz à propagação linear de um reservatório.
No método Muskingum, os parâmetros K e X são determinados por calibração usando registros de fluxo. As medições simultâneas de vazão de entrada e saída para um determinado trecho do canal são acopladas a um procedimento de tentativa e erro, levando à determinação de K e X (consulte o Exemplo 10-1). O procedimento é demorado e carece de capacidade preditiva. Os valores de K e X determinados desta maneira são válidos apenas para o evento de alcance e inundação fornecido na calibração. A extrapolação para outros trechos ou para outros eventos de inundação (de magnitude diferente) dentro do mesmo trecho geralmente não é justificável.
Quando dados suficientes estão disponíveis, uma calibração pode ser realizada para vários eventos de inundação, cada um com magnitude diferente, para cobrir uma ampla gama de níveis de inundação. Desta forma, a variação de K e X em função do nível de inundação pode ser verificada. Na prática, K é mais sensível ao nível de inundação do que X. Um esboço da variação de K com nível d'água e vazão é mostrado na Fig. 10-14.

Desenho esquemático do tempo de viagem em função da vazão e do nível d'água

Fig. 10-14 Desenho esquemático do tempo de viagem em função da vazão e do nível d'água.

Exemplo 10-1.
Um hidrograma de entrada do escoamento para um trecho do canal é mostrado na Col. 2 da Tabela 10-4. Suponha que o escoamento de base seja de 352 m³/s. Usando o método Muskingum, direcione esse hidrograma através de um alcance de canal com K = 2 d e X = 0,1 para calcular um hidrograma de vazão.

Primeiro, é necessário selecionar um intervalo de tempo Δt. Neste caso, é conveniente escolher Δt = 1 d. Como na propagação do reservatório, a razão entre o tempo e o pico do intervalo de tempo (t_p /Δt) deve ser maior ou igual a 5. Além disso, o intervalo de tempo escolhido deve ser tal que os coeficientes de propagação permaneçam positivos. Com Δt = 1 d, K = 2 d, e X = 0,1, os coeficientes de encaminhamento (Eq. 10-93) são: C₀ = 0,1304; C₁ = 0,3044; e C₂ = 0,5652. Verifica-se que C₀ + C₁ + C₂ = 1. Os cálculos de propagação são mostrados na Tabela 10-4.

A coluna 1 mostra a hora em dias.
A coluna 2 mostra as ordenadas do hidrograma de escoamento de entrada em metros cúbicos por segundo.
As colunas 3-5 mostram os escoamentos parciais.
Após a Eq. 10-91, as Cols. 3 a 5 são somadas para obter a Col. 6, que são as ordenadas do hidrograma de saída em metros cúbicos por segundo.

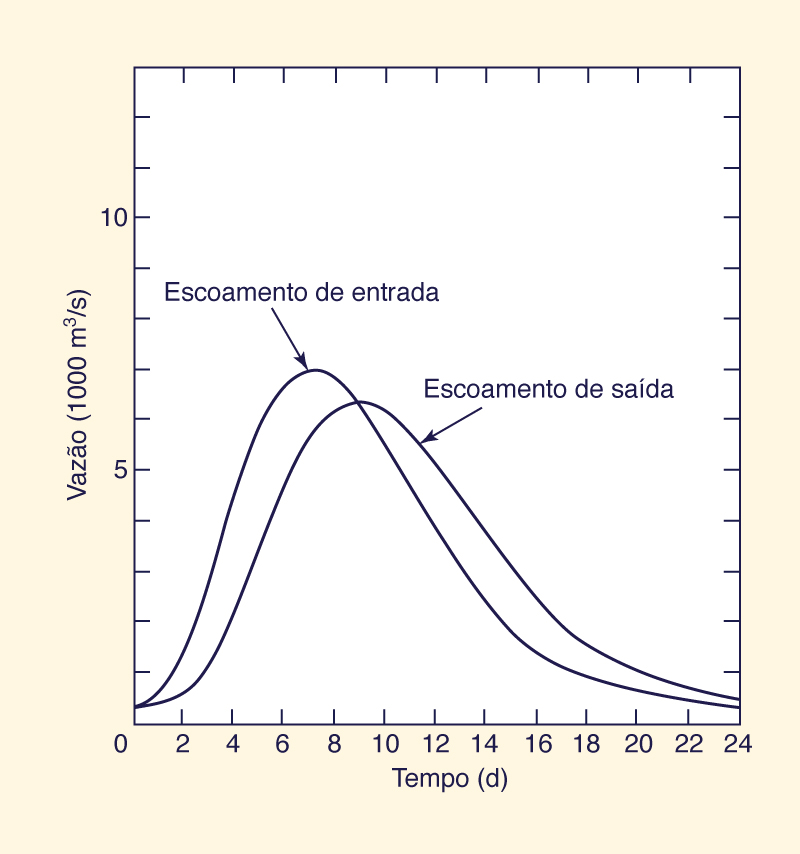
Para explicar brevemente o procedimento, presume-se que a vazão no início (dia 0) seja igual à entrada no início: 352 m³/s. A entrada no dia 1 multiplicada por C₀ é inserida na Col. 3, dia 1: 76,6 m³/s. A entrada no dia 0 multiplicada por C₁ é inserida na coluna 4, dia 1: 107,1 m³/s. A vazão no dia 0 multiplicada por C₂ é inserida na Col. 5, dia 1: 199 m³/s. As colunas 3-5 do dia 1 são somadas para obter a Col. 6 do dia 1: 76,6 + 107,1 + 199,0 = 382,7 m³/s. Os cálculos prosseguem de maneira recursiva até que todas as saídas na Col. 6 tenham sido obtidas. Os hidrogramas de entrada e saída são plotados na Fig. 10-15. O pico de vazão é de 6352,6 m³/s, o que mostra que o pico de entrada, 6951 m³/s, atenuou cerca de 91% do seu valor inicial. O pico de vazão ocorre no dia 9, 2 d após o pico de entrada, que ocorre no dia 7. O tempo decorrido entre a ocorrência do pico de entrada e o pico de saída é geralmente igual a K, o tempo de viagem.

Tabela 10-4 Propagação de canais pelo Método de
Muskingum: Exemplo 10-1.

(1) (2) (3) (4) (5) (6)

Tempo
(h) Escoamento
de entrada
(m³/s) Escoamentos Parciais (m³/s) Escoamento
de saída
(m³/s)

C₀I₂ C₁I₁ C₂I₁

0 352,0 ___ ___ ___ 352,0

1 587,0 76,6 107,1 199,0 382,7

2 1353,0 176,5 178,6 216,3 571,4

3 2725,0 355,4 411,8 323,0 1090,2

4 4408,5 575,0 829,4 616,2 2020,6

5 5987,0 780,9 1341,7 1142,1 3264,7

6 6704,0 874,4 1822,1 1845,3 4541,8

7 6951,0 906,7 2040,3 2567,1 5514,1

8 6839,0 892,0 2115,5 3116,7 6124,2

9 6207,0 809,6 2081,5 3461,5 6352,6

10 5346,0 697,3 1889,1 3590,6 6177,0

11 4560,0 594,8 1627,0 3491,4 5713,2

12 3861,5 503,7 1387,8 3229,2 5120,7

13 3007,0 392,2 1175,2 2894,3 4461,7

14 2357,5 307,5 915,2 2521,8 3744,5

15 1779,0 232,0 717,5 2116,5 3066,0

16 1405,0 183,3 541,4 1733,0 2457,7

17 1123,0 146,5 427,6 1389,1 1963,2

18 952,5 124,2 341,8 1109,6 1575,6

19 730,0 95,2 289,9 890,6 1275,7

20 605,0 78,9 222,2 721,0 1022,1

21 514,0 67,1 184,1 577,7 828,9

22 422,0 55,1 156,4 468,5 680,0

23 352,0 45,9 128,4 384,4 558,7

24 352,0 45,9 107,1 315,8 468,8

25 352,0 45,9 107,1 265,0 418,0

Propagação do canal pelo Método de Muskingum

Fig. 10-15 Propagação do canal pelo Método de Muskingum:
Exemplo 10-1.

calculator image
CÁLCULO ONLINE. Usando ONLINE ROUTING04, a resposta é essencialmente a mesma da Col. 6, Tabela 10-4.

O Exemplo 10-1 ilustrou o estágio preditivo do método Muskingum, no qual os parâmetros de propagação são conhecidos antes da propagação, propriamente dita. Se os parâmetros não forem conhecidos, é necessário primeiro executar uma calibração. O procedimento de tentativa e erro para calibrar os parâmetros de propagação é ilustrado pelo Exemplo 10-2.

Exemplo 10-2.
Utilizar o hidrograma de saída calculado no exemplo anterior em conjunto com o hidrograma de entradada de escoamente que foi dado para calibrar o método Muskingum, isto é, para encontrar os parâmetros de propagação K e X .

O procedimento está resumido na Tabela 10-5.

A coluna 1 mostra a hora em dias.
A coluna 2 mostra o hidrograma de entrada em metros cúbicos por segundo.
A coluna 3 mostra o hidrograma de vazão em metros cúbicos por segundo.
A coluna 4 mostra o armazenamento do canal em (metros cúbicos por segundo-dias.
O armazenamento do canal no início é assumido como 0 e esse valor é inserido na Col. 4, dia 0.

O armazenamento do canal é calculado resolvendo-se a Eq. 10-89 para S₂:

S₂ = S₁ + ( Δt / 2 ) ( I₁ + I₂ - O₁ - O₂ )

São feitas várias tentativas de X, dentro do intervalo de 0,0 a 0,5, por exemplo, 0,1, 0,2 e 0,3.
Para cada valor experimental de X, os fluxos ponderados [ XI + ( 1 - X ) O] são calculados, conforme mostrado nas Cols. 5-7.
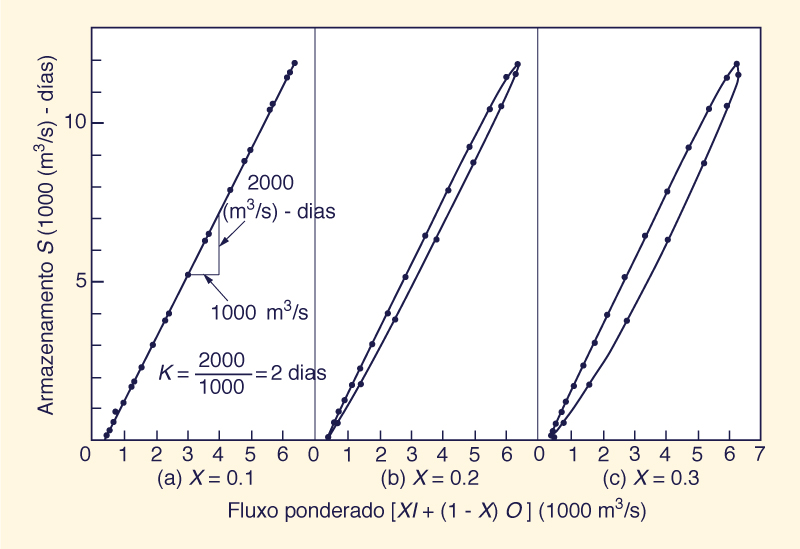
Cada um dos fluxos ponderados é plotado contra o armazenamento de canal (Col. 4), conforme mostrado na Fig. 10-16.
O valor de X para que o armazenamento de dados de fluxo contra parcelas ponderados mais próximos de uma linha é tomada como o valor correto de X. Neste caso, Fig. 10-16 (a): X = 0,1 é escolhido.
Segundo a Eq. 10-88, o valor de K é obtido a partir da Fig. 10-16 (a) calculando a inclinação da curva de armazenamento versus a vazão ponderada.
In this case, the value of K = [2000 (m³/s)-d]/(1000 m³/s) = 2 d.
Nesse caso, o valor de K = [2000 (m 3 / s) -d] / (1000 m 3 / s) = 2 d.
Assim, observa-se que K = 2 dias e X = 0,1 são os parâmetros de propagação de Muskingum para os hidrogramas de entrada e saída dados.

Tabela 10-5 Calibração do parâmetro de propagação de Muskingum: Exemplo 10-2.

(1) (2) (3) (4) (5) (6) (7)

Tempo
(h) Escoamento
de entrada
(m³/s) Escoamento
de saída
(m³/s) Armazenamento
(m³/s)-d Escoamento Ponderado (m³/s)

X = 0,1 X = 0,2 X = 0,3

0 352,0 352,0 0 ___ ___ ___

1 587,0 382,7 102,2 403,0 423,5 443,9

2 1353,0 571,4 595,2 649,6 727,7 805,9

3 2725,0 1090,2 1803,4 1253,7 1417,2 1580,6

4 4408,5 2020,6 3814,7 2259,4 2498,2 2737,0

5 5987,0 3264,7 6369,8 3536,9 3809,2 4081,4

6 6704,0 4541,8 8812,1 4758,0 4974,2 5190,5

7 6951,0 5514,1 10611,6 5657,8 5801,5 5945,2

8 6839,0 6124,2 11687,5 6195,7 6267,2 6338,6

9 6207,0 6352,6 11972,1 6338,0 6323,5 6308,9

10 5346,0 6177,0 11483,8 6093,9 6010,8 5927,7

11 4560,0 5713,2 10491,7 5597,9 5482,6 5367,2

12 3861,5 5120,7 9285,5 4994,8 4868,9 4742,9

13 3007,0 4461,7 7928,5 4316,2 4170,8 4025,3

14 2357,5 3744,5 6507,7 3605,8 3467,1 3328,4

15 1779,0 3066,0 5170,7 2937,3 2808,6 2679,9

16 1405,0 2457,7 4000,8 2352,4 2247,2 2141,9

17 1123,0 1963,2 3054,4 1879,2 1795,2 1711,1

18 952,5 1575,6 2322,7 1513,4 1451,1 1388,7

19 730,0 1275,7 1738,2 1221,1 1166,6 1112,0

20 605,0 1022,1 1256,8 980,4 938,7 897,0

21 514,0 828,9 890,8 797,4 765,9 734,4

22 422,0 680,0 604,4 654,2 628,4 602,6

23 352,0 558,7 372,0 537,9 517,3 496,6

24 352,0 468,8 210,3 457,1 445,4 433,8

25 352,0 418,0 118,9 411,4 404,8 398,2

Calibração do parâmetro de propagação de Muskingum

Fig. 10-16 Calibração do parâmetro de propagação de Muskingum: Exemplo 10-2.

A estimativa dos parâmetros de propagação é crucial para a aplicação do método Muskingum. Os parâmetros não são constantes, tendendo a variar com a vazão. Se os parâmetros de propagação puderem ser relacionados às características de escoamento e do canal, a necessidade de calibração por tentativa e erro será eliminada. O parâmetro K pode ser relacionado ao comprimento e velocidade da onda de inundação, enquanto X pode estar relacionado às características de difusividade do escoamento e canal. Essas proposições são a base do método Muskingum-Cunge.

10.6 MÉTODO DE MUSKINGUM-CUNGE

[Ondas Dinâmicas]   [Questões]   [Problemas]   [Referências]   •   [Topo]   [Equações Governantes]   [Solução Linear]   [Ondas Cinemáticas]   [Ondas Difusivas]   [Método de Muskingum]

O método Muskingum requer uma calibração para identificar os parâmetros de propagação (Exemplo 10-2). O procedimento é baseado em hidrogramas de entrada e saída medidos, conforme mostrado nas Cols. 2 e 3 da Tabela 10-5. Portanto, uma estação de medição é uma necessidade absoluta para que o método Muskingum seja usado adequadamente. Isso limita a aplicação do método aos trechos que possuem uma estação de monitoramento de escoamento contínuo.
Diferentemente do método Muskingum, o método Muskingum-Cunge requer dados hidráulicos, e não hidrológicos, para calcular os parâmetros de propagação. Os dados hidráulicos consistem em dados físicos, como inclinação do canal e características da seção transversal. Assim, o método Muskingum-Cunge não exige explicitamente uma estação de monitoramento do escoamento, sendo aplicável a qualquer trecho de canal desde que os dados físicos estejam disponíveis.
O método Muskingum é obtido pela combinação da equação diferencial de armazenamento, ou seja, a equação de continuidade expressa na forma diferencial total (Eq. 10-87) com uma relação linear de entrada/saída/armazenamento (Eq. 10-88). Isso leva à equação de propagação de Muskingum (Eq. 10-92) com coeficientes de propagação adequados (Eq. 10-93). O método Muskingum-Cunge é derivado discretizando a equação da onda cinemática (Eq. 10-55) em um modo linear, de maneira semelhante à do método Muskingum, que leva à mesma equação de propagação. Os coeficientes, no entanto, são definidos com base nas características mensuráveis do canal.
As semelhanças parecem terminar aí. O método Muskingum é agrupado através do trecho do canal, com base no armazenamento e é capaz de descrever a difusão das ondas de inundação (Exemplo 10-1). O método Muskingum-Cunge é distribuído, com dados especificados em seções transversais, e com base em uma discretização da equação da onda cinemática, que ostensivamente não se difunde. No entanto, cálculos reais usando o método Muskingum-Cunge mostram que ele é capaz de descrever a difusão de ondas, de maneira semelhante ao método Muskingum.
Cunge (1969) traçou a difusão do analógico discretizado da equação da onda cinemática à difusão numérica do próprio esquema (ver quadro). Assim, ele foi capaz de explicar o paradoxo. Os métodos Muskingum e Muskingum-Cunge têm a mesma base teórica. Os parâmetros de propagação do método Muskingum são hidrológicos, baseados no armazenamento e determinados por calibração usando dados de escoamento. Os parâmetros de propagação do método Muskingum-Cunge são hidráulicos, distribuídos (em uma seção transversal) e baseados exclusivamente em dados físicos.

Uma palavra de explicação sobre o conceito de difusão numérica ¹

A existência de difusão em um esquema numérico precisa de mais elaboração. Como Hayami (1951) apontou, na natureza as irregularidades produzem difusão física. O mesmo processo se estende ao mundo computacional: Irregularidades produzem difusão numérica. As irregularidades são interpretadas como os erros inerentes à computação numérica, entre os quais os erros de truncamento se destacam primordialmente. A substituição de uma equação diferencial parcial, baseada em ∂ por uma equação de diferença finita, baseada em Δ resulta em erros que, quando considerados em conjunto, se manifestam como difusão. Assim, a difusão numérica é no mundo computacional o que é a difusão física no mundo real.
¹ Veja Cunge (1969) para um tratamento detalhado da difusão numérica em conexão com o método Muskingum.

Equação de propagação Muskingum-Cunge
Para derivar a equação de propagação de Muskingum-Cunge, a equação de onda cinemática (Eq. 10-55) é discretizada no planox-t (Fig. 10-17) de uma maneira que se assemelha ao método de Muskingum, centralizando a derivada espacial e descentralizando a derivada temporal por meio de um fator de ponderação X:

  X (Q_jⁿ⁺¹ - Q_jⁿ ) + (1 - X) (Q_j+1ⁿ⁺¹ - Q_j+1ⁿ )
^{________________________________________________} +
                                       Δt

      (Q_j+1ⁿ - Q_jⁿ ) + (Q_j+1ⁿ⁺¹ - Q_jⁿ⁺¹ )
c ^{_______________________________________} = 0
                                  2 Δx
(10-94)

Em que: c = βV é a celeridade da onda cinemática.

Discretização no espaço-tempo da equação da onda cinemática em paralelo ao método Muskingum

Fig. 10-17 Discretização no espaço-tempo da equação da onda cinemática
em paralelo ao método Muskingum.

Resolvendo a Eq. 10-94 para a vazão desconhecida leva à seguinte equação de propagação:

Q _j+1 ⁿ⁺¹ = C₀ Q_j ⁿ⁺¹ + C₁ Q_j ⁿ + C₂ Q_j+1 ⁿ
(10-95)

Os coeficientes de propagação são:

                c ( Δt / Δx ) - 2X
C₀ = ^{________________________}
            2(1 - X) + c ( Δt / Δx )
(10-96a)

                c ( Δt / Δx ) + 2X
C₁ = ^{________________________}
            2(1 - X) + c ( Δt / Δx )
(10-96b)

            2(1 - X) - c ( Δt / Δx )
C₂ = ^{________________________}
            2(1 - X) + c ( Δt / Δx )
(10-96c)

Definindo o tempo de viagem como:

           Δx
K = ^______
            c
(10-97)

Observa-se que os conjuntos de Eq. 10-93 e Eq. 10-96 são os mesmos. A Equação 10-97 confirma que K é de fato o tempo de viagem da onda de inundação, ou seja, o tempo que uma determinada vazão leva para percorrer o comprimento do trecho Δx com a celeridade da onda cinemática c.
Propriedades numéricas
O número de Courant é definido como a razão entre a celeridade física (c) e a celeridade numérica ou em grade Δx /Δt.. Portanto:
                Δt
C = c ^______
                Δx
(10-98)

A equação 10-95 é um análogo numérico da Eq. 10-55 e, portanto, sujeito à difusão e dispersão numérica. Difusão numérica é o erro de segunda ordem; dispersão numérica é o erro de terceira ordem. As seguintes condições são válidas:

Para X = 0.5 e C = 1, a equação de propagação tem precisão de terceira ordem, ou seja, a solução numérica é igual à solução analítica (da equação de onda cinemática).
Para X = 0,5 e C ≠=1, a equação de propagação tem precisão de segunda ordem, exibindo apenas dispersão numérica.
Para X < 0,5 e C ≠ 1, a equação de propagação tem precisão de primeira ordem exata, exibindo tanto difusão numérica quanto dispersão.
Para X < 0,5 e C = 1, a equação de propagação tem precisão de primeira ordem, exibindo apenas difusão numérica.

Essas relações estão resumidas na Tabela 10-6.

Tabela 10-6 Propriedades numéricas do método de Muskingum-Cunge.

Paâametro
X ParametePaâametro
C Ordem de
Precisão Difusão
Numérica Dispersão
Numérica

0,5 1 Terceira Não Não

0,5 ≠ 1 Segunda Não Sim

< 0,5 ≠ 1 Primeira Sim Sim

< 0,5 1 Primeira Sim Não

Na prática, a difusão numérica pode ser usada para simular a difusão física da onda de inundação real. Ao expandir a função discreta Q (jΔx, n Δt)Q na série de Taylor sobre o ponto de grade (jΔx, n Δt), é obtido o coeficiente de difusão numérico do esquema de Muskingum (Cunge, 1969) (Apêndice B):

                      1
ν_n = c Δx ( ^____ - X )
                      2

(10-99)

Na qual, ν_n é o coeficiente de difusão numérico do método de Muskingum. Esta equação revela o seguinte:
Para X = 0,5, não há difusão numérica, embora haja alguma dispersão numérica para C ≠ 1;
Para X > 0,5, o coeficiente de difusão numérico é negativo, ou seja, amplificação numérica, o que explica o comportamento do método Muskingum para essa faixa de valores X;
Para Δx = 0, o coeficiente de difusão numérico é zero, claramente o caso trivial.

Uma equação preditiva para X pode ser obtida combinando à difusividade hidráulica ν_h (Eq. 10-83) com o coeficiente de difusão numérico do método de Muskingum ν_h (Eq. 10-99). Isso leva à seguinte expressão para X:

          1                   q_o
X = ^___ ( 1 - ^__________ )
          2              S_o c Δx
(10-100)

Com X calculado pela Eq. 10-100, o método Muskingum é referido como método Muskingum-Cunge. Assim, o parâmetro de propagação X pode ser calculado em função das seguintes propriedades numéricas e físicas:
Comprimento do trecho Δx,
Vazão de referência por unidade de largura q_o,
Celeridade das ondas cinemáticas c, e
Declividade do leito (inferior) S_o.

Observa-se que a Eq. 10-100 foi derivada pela combinaç:ão da difusão física com a numérica (um processo de segunda ordem) e não é responsável pela dispersão (um processo de terceira ordem). Portanto, para simular a difusão de ondas adequadamente com o método Muskingum-Cunge, é necessário otimizar a difusão numérica (com as Eq. 10-100) e, ao mesmo tempo, minimizar a dispersão numérica mantendo o valor de C ≅ 1.

Vantagem do método Muskingum-Cunge

Uma característica exclusiva do método Muskingum-Cunge, que o diferencia de outros modelos numéricos de ondas cinemáticas, é a independência da grade do hidrograma de vazão calculado. Se a dispersão numérica for minimizada, a vazão calculada na extremidade à jusante de um trecho de canal será essencialmente a mesma, independentemente de quantas sub-trechos forem usados no cálculo. Isso ocorre porque X é uma função de Δx e os coeficientes de propagação C₀, C₁, e C₂ em concordância.

Uma versão melhorada do método Muskingum-Cunge é devida a Ponce e Yevjevich (1978). A difusividade da grade é definida como a difusividade numérica para o caso de X = 0. Da Eq. 10-99, a difusividade da grade é:

               Δx
ν_g = c ^_____
                2
(10-101)

A célula Reynolds número D é definida como a razão de difusividade hidráulica (Eq. 10-83) para difusividade da grade (Eq. 10-101). Isto leva a:

               q_o
D = ^__________
           S_o c Δx
(10-102)

Assim sendo:

          1
X = ^___ ( 1 - D )
          2
(10-103)

As Eqs. 10-101 e 10-102 implicam que, para valores muito pequenos de Δx, D pode ser maior do que 1, levando a valores negativos de X. De fato, para o comprimento do trecho característico, o número de Reynolds célula é D = 1 e X.

                 q_o
Δx_c = ^________
               S_o c
(10-104)

Assim sendo, no método de Muskingum-Cunge, comprimentos de trechos mais curtos do que o comprimentodo trecho característica resultam em valores negativos de X. Isso deve ser contrastado com o método clássico de Muskingum (Seção 10.4), no qual X é restrito na faixa de 0,0 ≤ X 0,5. No Muskingum clássico, X é interpretado como um fator de ponderação. Como mostrado pelas Eqs. 10-101 e 10-102, os valores não negativos de X estão associados a trechos longos, típicos de cálculos manuais usados no desenvolvimento e na aplicação precoce do método Muskingum.
No método Muskingum-Cunge, no entanto, X é interpretado de forma combinada ao momento ou como fator combinado à difusão. Portanto, valores negativos de X são inteiramente possíveis. Esse recurso permite o uso de trechos mais curtos do que seria possível se X fosse restrito aos valores não negativos.
Coeficientes de propagação
A substituição das Eqs. 10-98 e 10-100 na Eq. 10-96 leva a coeficientes de propagação expressos em termos de números de Courant e de de Reynolds:

             -1 + C + D
C₀ = ^{______________}
              1 + C + D
(10-105a)

              1 + C - D
C₁ = ^{______________}
              1 + C + D
(10-105b)

              1 - C + D
C₂ = ^{______________}
              1 + C + D
(10-105c)

O cálculo dos parâmetros de propagação C e D pode ser realizado de várias maneiras. A celeridade das ondas pode ser calculada com a Eq. 10-57 ou Eq. 10-59. Com Eq. 10-57, c = βV; with Eq. 10-59, c = (1/T) dQ/dy. Teoricamente, essas duas equações são iguais. Para aplicações práticas, se houver dados sobre a curva-chave e geometria da seção transversal (ou seja, tabelas da largura do topo da vazão e nível d'água), a Eq. 10-59 é preferível do que a Eq. 10-57, porque responde diretamente pelo formato da seção transversal. Na ausência de uma curva-chave e de dados tda seção, a Eq. 10-57 pode ser usada para estimar a celeridade das ondas de inundação.
Com a ajuda de Eqs. 10-98 e 10-102, os parâmetros de propagação podem ser baseados nas características do escoamento. Os cálculos podem prosseguir de modo linear ou não linear. No modo linear, os parâmetros de propagação são baseados em valores de fluxo de referência e mantidos constantes durante todo o cálculo no tempo. A escolha do fluxo de referência influencia os resultados calculados, embora o efeito geral seja pequeno (Ponce e Yevjevich, 1978) Para aplicações práticas, um valor de fluxo médio ou de pico pode ser usado como fluxo de referência. O valor do pico de fluxo tem a vantagem de poder ser prontamente determinado, embora uma melhor aproximação possa ser obtida usando um valor médio. O modo linear de computação é referido como o método Muskingum-Cunge de parâmetro constante para distingui-lo do método Muskingum-Cunge de parâmetro variável, no qual os parâmetros de propagação podem variar com o fluxo. O método de parâmetro constante se assemelha ao método de Muskingum, com a diferença de que os parâmetros de propagação são baseados em características mensuráveis do fluxo e do canal, e não em dados históricos de fluxo.

Exemplo 10-3.
Use o método Muskingum-Cunge de parâmetro constante para propagar uma onda de inundação com as seguintes características da inundação e do canal: vazão de pico Q_p = 1000 m³/s; escoamento base Q_b, = 0 m³/s; declividade do fundo do canal S_o = 0,000868; área de escoamento com vazão máxima A_p = 400 m²; largura no topo durante a vazão de pico de descarga T_p = 100 m; expoente de classificação β = 1,6; comprimento do trecho Δx = 14,4 km; intervalo de tempo Δt = 1 h.

Tempo (h) 0 1 2 3 4 5 6 7 8 9 10

Escoamento (m³/s 0 200 400 600 800 1000 800 600 400 200 0

A velocidade média (com base na vazão de pico) é V = Q_p/A_p = 2,5 m/s. A celeridade das ondas é c = βV = 4 m/s. A vazão por unidade de largura (com base no pico de descarga) é q_o = Q_p/T_p = 10 m²/s. O número de Courant (Eq. 10-98) é C = 1. O número de Reynolds da célula (Eq. 10-102) é D = 0,2. Os coeficientes de propagação (Eq. 10-105) são C₀ = 0,091; C₁ = 0,818; e C₂ = 0,091. Confirma-se que a soma dos coeficientes de propagação é igual a 1. Os cálculos de propagação são mostrados na Tabela 10-7.

Tabela 10-7 Propagação do canal pelo Método de Muskingum-Cunge, Exemplo 10-2.

(1) (2) (3) (4) (5) (6)

Tempo
(h) Escoamento
de entrada
(m³/s) Escoamentos parciais (m³/s) Escoamento
de saída
(m³/s)

C₀ I₂ C₁ I₁ C₂ I₁

0 0 ___ ___ ___ 0,0

1 200 18,2 0,0 0,0 18,20

2 400 36,4 163,6 1,66 201,66

3 600 54,6 327,2 18,35 400,15

4 800 72,8 490,8 36,41 600,01

5 1000 91,0 654,4 54,60 800,00

6 800 72,8 818,0 72,80 963,60

7 600 54,6 654,4 87,69 796,69

8 400 36,4 490,8 72,50 599,70

9 200 18,2 327,2 54,57 399,97

10 0 0,0 163,6 36,40 200,00

11 0 0,0 0,0 18,20 18,20

12 0 0,0 0,0 1,66 1,66

13 0 0,0 00,0 0,16 0,16

calculator image
CÁLCULO ONLINE. Usando ONLINE ROUTING05, a resposta é essencialmente a mesma da Col. 6, Tabela 10-7.

Requisitos de resolução
Ao usar o método Muskingum-Cunge, deve-se tomar cuidado para garantir que os valores de Δx e Δt sejam suficientemente pequenos para se aproximarem da forma real do hidrograma. Para hidrogramas em subida suave, é recomendado um valor mínimo de t_p /Δt = 5. Esse requisito geralmente resulta na resolução da base de tempo do hidrograma em pelo menos 15 a 25 pontos discretos, considerados adequados para a propagação de Muskingum.
Diferentemente da resolução temporal, não há critérios definidos para a resolução espacial. Um critério confirmado pela experiência baseia-se no fato de que os números de Courant e da célula de Reynolds estão inversamente relacionados ao comprimento do trecho Δx. Portanto, para manter Δx suficientemente pequeno, os números de Courant e da célula de Reynolds devem ser mantida suficientemente grandes. Isso leva ao critério prático (Ponce e Theurer, 1982):

C + D ≥ 1
(10-106)

A Eq. 10-106 também pode ser escrita da seguinte forma: -1 + C + D ≥ 0. Isso confirma a necessidade de evitar valores negativos de C 0 no propagação Muskingum-Cunge (consulte a Eq. 10-105a). A experiência mostrou que valores negativos de C₁ or C₂ não afetam adversamente a precisão geral do método.
Não obstante a Eq. 10-106, o método Muskingum-Cunge funciona melhor quando a dispersão numérica é minimizada, ou seja, quando C ≅ 1. Valores de C substancialmente menores que 1 provavelmente causam quedas notórias, ou saídas negativas, em porções do hidrograma calculado. Essa anomalia computacional é atribuída à dispersão numérica excessiva e deve ser evitada.

Método não linear de Muskingum-Cunge
A equação da onda cinemática, Eq. 10-55, não é linear porque a celeridade da onda cinemática varia com a vazão. A não linearidade é leve, entre outras coisas, porque a variação da celeridade das ondas geralmente é restrita dentro de uma faixa estreita. No entanto, em certos casos, pode ser necessário considerar essa não linearidade. Isso pode ser feito de duas maneiras: (1) durante a discretização, permitindo que a celeridade das ondas varie, resultando em um esquema numérico não linear a ser resolvido por meios iterativos; e (2) após a discretização, variando os parâmetros de propagação, como no método de parâmetro variável Muskingum-Cunge (Ponce e Yevjevich, 1978. A última abordagem é particularmente útil se o efeito não linear geral for pequeno, o que geralmente ocorre.
O método Muskingum-Cunge do parâmetro variável representa uma melhoria pequena, mas às vezes perceptível, em relação ao método de parâmetro constante. As diferenças provavelmente são mais acentuadas para trechos muito longos e/ou grandes variações nos níveis de escoamento. Os hidrogramas de inundação calculados com parâmetros variáveis mostram uma certa distorção, seja a declividade das ondas, no caso de fluxos contidos nas margens ou com a atenuação das ondas (achatamento) no caso dos fluxos típicos de transbordamento das margens. Esta é uma manifestação física do efeito não linear, ou seja, diferentes níveis de fluxo viajando com diferentes celeridades. Por outro lado, os hidrogramas de inundação calculados usando parâmetros constantes não mostram distorção das ondas.

Avaliação do método Muskingum-Cunge
O método Muskingum-Cunge é uma alternativa baseada fisicamente ao método Muskingum. Ao contrário do método Muskingum, onde os parâmetros são calibrados usando dados de fluxo, no método Muskingum-Cunge os parâmetros são calculados com base nas características do fluxo e do canal. Isso possibilita o propagação de canais sem a necessidade de calibração de parâmetros de forma complexa por um longo período de tempo. Mais importante, torna possível a propagação extensiva de canais em fluxos não monitorados com uma expectativa razoável de precisão. Com o recurso de parâmetro variável, propriedades não lineares das ondas de inundação (que só poderiam ser obtidas por meio de procedimentos numéricos mais elaborados) podem ser descritas no contexto da formulação de Muskingum.
Como o método Muskingum, o método Muskingum-Cunge é limitado para ondas de difusão. Além disso, o método Muskingum-Cunge é baseado em uma classificação de valor único e não leva em conta a não-uniformidade do fluxo elevado ou os fluxos instáveis, mostrando laços (loops) substanciais na classificação da curva-chave (como exemplo, as ondas dinâmicas). Assim, o método Muskingum-Cunge é adequado para a propagação de canais em riachos naturais sem efeitos significativos de remanso e para fluxos instáveis que se classificam sob o critério de ondas de difusão (Eq. 10-66).
Uma diferença importante entre os métodos Muskingum e Muskingum-Cunge deve ser observada. O método Muskingum é baseado no conceito de armazenamento (Eq. 10-87) e, portanto, é agrupado, com os parâmetros K e X sendo as médias dos trechos. O método Muskingum-Cunge, no entanto, é distribuído na natureza, com os parâmetros C e D baseados nos valores avaliados nas seções transversais do canal. Portanto, para que o método Muskingum-Cunge melhore o método Muskingum, é necessário que os parâmetros de propagação avaliados nas seções transversais do canal sejam representativos do alcance do canal em consideração (Fig. 10-18).
Historicamente, o método Muskingum foi calibrado usando dados de fluxo. Pelo contrário, o método Muskingum-Cunge baseia-se em características físicas como curvas-chave, dados da seção transversal e declividade do canal. Os diferentes requisitos de dados refletem as diferentes bases teóricas dos métodos, ou seja, o conceito de armazenamento concentrado no método Muskingum e a teoria da onda cinemática / difusão distribuída no método Muskingum-Cunge.

Rio Moyan

Fig. 10-18 Rio Moyan, em Lambayeque, no Peru.

10.7 ONDAS DINÂMICAS

[Questões]   [Problemas]   [Referências]   •   [Topo]   [Equações Governantes]   [Solução Linear]   [Ondas Cinemáticas]   [Ondas Difusivas]   [Método de Muskingum]   [Método de Muskingum-Cunge]

No fluxo instável de canal aberto, o termo onda dinâmica é usado para se referir a dois tipos diferentes de ondas:

Uma onda que negligencia o atrito e a declividade do leito, isto é, a onda [3] na Tabela 10-2, e
Uma onda que inclui todos os termos na equação do movimento, ou seja, onda [5] na Tabela 10-2.

Para evitar confusão, o primeiro tipo de onda [3] é referido aqui como uma verdadeira onda dinâmica. O segundo tipo [5] é chamado de onda cinemático-dinâmica mista, para ondas dinâmicas mistas curtas.

Ondas dinâmicas verdadeiras
Conceitualmente, as verdadeiras ondas dinâmicas são exatamente o oposto das ondas cinemáticas. Enquanto as ondas cinemáticas estão do lado esquerdo do espectro do número de onda, as verdadeiras ondas dinâmicas estão do lado direito (Fig. 10-3). Assim, seu número de onda adimensional é longo, ou seja, o comprimento de onda L é curto em relação ao comprimento do canal de referência L_o (Eq. 10-30).
Enquanto a celeridade relativa adimensional de uma onda cinemática é constante e igual a 0,5, a da onda dinâmica verdadeira é igual à recíproca do número de Froude (Fig. 10-3):
              1          (gh_o)^1/2
c_drd = ^____ = ^_________
              F             u_o
(10-107)

A celeridade relativa de uma verdadeira onda dinâmica é:


c_rd = (gh_o)^1/2
               (10-108)

A celeridade de uma verdadeira onda dinâmica é:

c_d = u_o ± (gh_o)^1/2
               (10-109)

Portanto, uma verdadeira onda dinâmica possui dois componentes, com celebridades:

c_d_₁ = u_o + (gh_o)^1/2
               (10-110a)


c_d_₂ = u_o - (gh_o)^1/2
               (10-110b)

As ondas cinemáticas e dinâmicas verdadeiras compartilham uma propriedade distinta: elas não atenuam. Isso ocorre devido à constância da celeridade relativa da onda adimensional dentro da faixa aplicável de número de onda adimensional (Fig. 10-3).
Na prática, ondas dinâmicas verdadeiras se aplicam às ondas curtas que podem estar presentes em canais de laboratório e pequenos canais. Eles não se aplicam às ondas de inundação, que ficam no lado esquerdo do espectro de número de onda adimensional.

Ondas dinâmicas mistas
As ondas cinemático-dinâmicas mistas , para ondas dinâmicas mistas curtas, ficam no meio do espectro do número de onda (Fig. 10-3). Conceitualmente, são o tipo mais completo de onda, porque consideram todos os termos da equação do movimento (Tabela 10-2). No entanto, para os números Vedernikov V < 1, (correspondentes aos números Froude F < 2 sob atrito Chezy em canais hidraulicamente amplos), as ondas dinâmicas mistas estão sujeitas à forte atenuação. A atenuação é mais forte no ponto de inflexão da celeridade relativa adimensional versus a função de número de onda adimensional (Fig. 10-4). A Fig. 10-5 mostra as taxas de atenuação, conforme descrito pelo decréscimo logarítmico δ.
Lighthill e Whitham (1955) descreveram a impermanência de ondas dinâmicas [mistas] nos seguintes termos:
"No caso de ondas de inundação, as ondas cinemáticas e dinâmicas [mistas] são possíveis juntas. No entanto, as ondas dinâmicas [mistas] têm uma velocidade de onda muito mais alta e também uma atenuação rápida. Portanto, embora qualquer distúrbio envie algum sinal à jusante na velocidade de onda comum para ondas longas de gravidade, esse sinal é muito fraco para ser percebido a uma distância considerável à jusante, e o sinal principal chega na forma de uma onda cinemática a uma velocidade muito mais lenta ".

Eles seguiram com esta afirmação (op. cit., page 291):
"Achamos desejável dar um tratamento matemático da competição entre ondas dinâmicas cinemáticas e [mistas] no fluxo do rio, a fim de mostrar quão completamente as ondas dinâmicas [mistas] estão subordinadas no caso de maior interesse, que é quando a velocidade do rio é bem subcrítica. Isso demonstra a inadequação das características da onda dinâmica [mista] como base para o cálculo ".

Assim, em geral, as ondas dinâmicas mistas não se aplicam aos fluxos de inundação em córregos naturais. Uma vez geradas, as ondas dinâmicas mistas tendem a se dissipar muito rapidamente, com sua massa se unindo à onda cinemática ou de difusão subjacente predominante.
A exceção pode ser uma onda de inundação gerada por uma brecha na barragem, que geralmente é tão repentina que pode ser efetivamente uma onda dinâmica mista. Essas ondas atenuam-se muito rapidamente, confirmando a correção da teoria. Por exemplo, considere a falha da barragem de Teton, em Idaho, em 5 de junho de 1976 (Fig. 10-19). A onda de inundação liberada no local da barragem atenuou uma pequena fração de sua força inicial (menos de 3%) a uma distância relativamente curta à jusante. Muitos outros exemplos de violações reais de barragens confirmaram que as ondas de inundação tendem a se dissipar rapidamente.

Ruptura na barragem de Teton

USBR
Fig. 10-19 Ruptura na barragem de Teton, no Idaho, EUA, em 5 de junho de 1976.

Modelagem de ondas dinâmicas mistas
Em relação à solução de uma onda dinâmica, as equações de continuidade e movimento são resolvidas por um procedimento numérico, (a) o método das diferenças finitas, (b) o método das características ou (c) o método dos elementos finitos. No método das diferenças finitas, as equações diferenciais parciais são discretizadas seguindo um esquema numérico escolhido. O método das características baseia-se na conversão do conjunto de equações diferenciais parciais em um conjunto relacionado às equações diferenciais ordinárias e na solução ao longo de uma grade característica, isto é, uma grade que segue as direções características. O método dos elementos finitos resolve um conjunto de equações integrais sobre uma grade escolhida de elementos finitos.
Nas últimas quatro décadas, o método das diferenças finitas passou a ser considerado a maneira mais conveniente de obter uma solução de ondas dinâmicas mistas para aplicações práticas. Entre vários métodos numéricos que foram usados em conexão com a onda dinâmica mista, a abordagem de Preissmann é provavelmente a mais popular (Liggett e Cunge, 1975). Este é um esquema de quatro pontos, centrado nas derivadas temporais e ligeiramente descentralizado nas derivadas espaciais, pelo uso de um fator de ponderação θ. A descentralização nas derivadas espaciais introduz uma pequena quantidade de difusão numérica necessária para controlar a estabilidade numérica do esquema não linear. Isso produz um esquema viável, mas suficientemente preciso.
As variáveis independentes usadas na propagação dinâmica de ondas mistas são geralmente a vazão Q e o nível d'água y. O canal de fluxo é dividido em várias subáreas para fins computacionais (Fig. 10-20). A aplicação da abordagem de Preissmann às equações governantes para as várias subáreas resulta em uma solução matricial que requer um algoritmo de varredura dupla, isto é, que é responsável apenas pelas entradas diferentes de zero da matriz do coeficiente, localizadas dentro de uma faixa estreita ao redor da diagonal principal (Liggett e Cunge, 1975). Essa técnica leva a uma economia considerável do tempo de armazenamento e da execução. Com as condições de contorno à montante e à jusante apropriadas (Fig. 10-20), a solução do conjunto de equações hiperbólicas marcha no tempo até que um número especificado de intervalos de tempo seja concluído.

A subdivisão do trecho para a propagação das ondas dinâmicas

Fig. 10-20 A subdivisão do trecho para a propagação das ondas dinâmicas.

Na prática, uma solução mista de ondas dinâmicas representa um aumento de ordem de magnitude na complexidade e nos requisitos de dados associados quando comparados às soluções de ondas cinemáticas ou de difusão. Seu uso é recomendado nas situações em que nem as soluções de ondas cinemáticas nem de difusão provavelmente representam adequadamente os fenômenos físicos. Particularmente, as soluções de ondas dinâmicas mistas são aplicáveis para as ondas de inundação de rompimento de barragens, vazão em encostas muito planas, vazão em grandes reservatórios, condições de marés fortes e reversões de vazão. Em geral, a onda dinâmica mista é recomendada para casos que garantam uma determinação precisa da variação instável dos estágios (níveis d'água) do rio.
A versão atual (Versão 5.0.7) do modelo HEC-RAS (US Army Corps of Engineers, 2020) contém um módulo de ondas dinâmicas adequado para aplicações práticas.
Curva de classificação dinâmica mista
Soluções de ondas dinâmicas mistas são frequentemente chamadas de propagação hidráulicao de rios. Como tal, eles têm a capacidade de calcular descargas e estágios instáveis quando apresentados com os dados de canal geométrico apropriados e condições iniciais e de contorno. Sua importância no fluxo instável é examinada aqui, comparando-as com ondas cinemáticas e de difusão.
As ondas cinemáticas calculam descargas instáveis; os estágios correspondentes são subsequentemente obtidos a partir das curvas de classificação apropriadas. Curvas de classificação de equilíbrio (constante, uniforme) são usadas para essa finalidade. Ondas de difusão podem ou não usar curvas de classificação de equilíbrio para calcular os estágios. Alguns métodos, por exemplo, Muskingum-Cunge, usam classificações de equilíbrio, mas soluções de ondas de difusão mais elaboradas não podem.
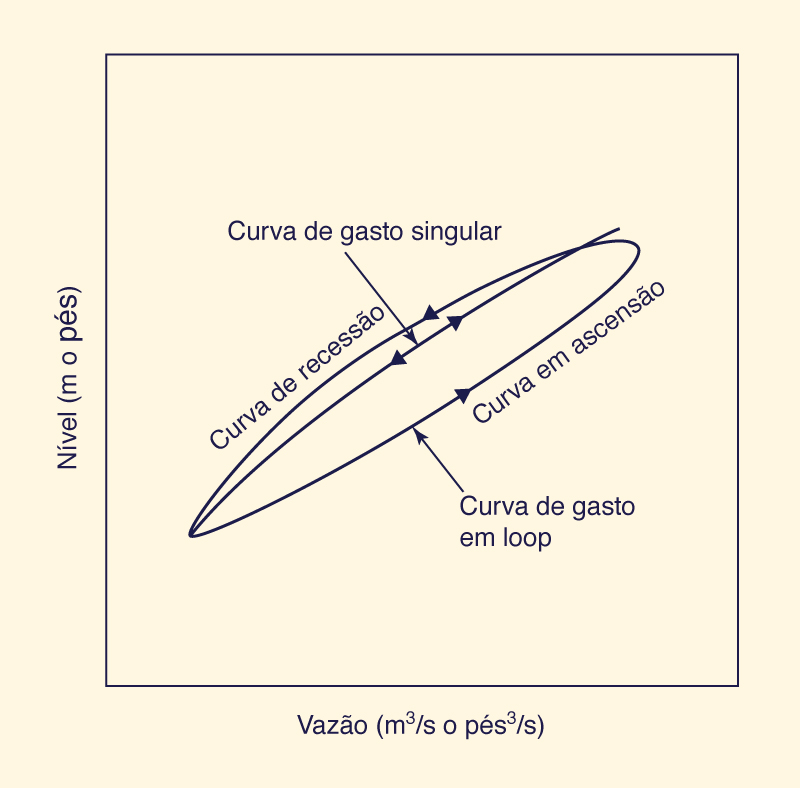
As ondas dinâmicas mistas dependem da física dos fenômenos incorporada nas equações que governam para gerar sua própria taxa de fluxo instável. Uma curva-chave em loop é produzida em cada seção transversal, como mostrado na Fig. 10-21. Para qualquer estágio, a vazão é maior no membro ascendente do hidrograma e menor no membro decrescente. Esse loop é devido a razões hidrodinâmicas e não deve ser confundido com outros loops, que podem ser causados por erosão, sedimentação ou alterações na configuração do leito.

Desenho esquemático da curva-chave em loop para ondas dinâmicas

Fig. 10-21 Desenho esquemático da curva-chave em loop para ondas dinâmicas.

A largura do loop é uma medida da instabilidade do fluxo, com loops mais largos correspondendo a um fluxo altamente instável. Se o loop for estreito, isso implica que o fluxo é levemente instável, sendo provavelmente uma onda de difusão. Se o loop for praticamente inexistente, o fluxo pode ser aproximado como fluxo cinemático. De fato, a suposição básica do fluxo cinemático é de que o momento pode ser simulado como fluxo uniforme constante, ou seja, que a curva de classificação é de valor único.
As observações anteriores levam à conclusão de que a importância das ondas dinâmicas mistas está diretamente relacionada à instabilidade do fluxo e ao loop associado na curva-chave. Para fluxos altamente instáveis, como ondas de inundação de barragens, pode muito bem ser a única maneira de contabilizar adequadamente a curva em loop. Para outros fluxos menos instáveis, as ondas cinemáticas e de difusão são uma alternativa viável, desde que a sua aplicação (Eqs. 10-67 e 10-84, respectivamente) possa ser claramente demonstrada.
Condição de contorno à jusante
A modelagem de uma onda dinâmica mista apresenta um paradoxo interessante: para resolver o problema corretamente, uma condição de contorno dinâmico à jusante (geralmente uma curva-chave) deve ser especificada. No entanto, uma condição de contorno à jusante dinâmica não é conhecida a priori . Segundo Abbott (1976):
"Uma fonte comum de erro é o uso de uma condição de contorno em um modelo dinâmico que é realmente adequado apenas para um modelo cinemático puro ... mas em um modelo dinâmico, a própria solução gera diferentes relações na curva-chave (vazão e nível d'água) de acordo com as variabilidades dos escoamentos, de modo que uma relação única de contorno contradiga a solução no limite de contorno. Um modelo finamente equilibrado geralmente fica instável nessa situação. No entanto, os modelos com forte amortecimento numérico podem sobreviver, apenas para fornecer resultados errôneos ".

Uma saída para essa dificuldade é estender artificialmente o canal em város subtrechos à jusante e especificar uma curva cinemática no limite à jusante recém-definido, dando ao loop a chance de se desenvolver na seção transversalà montante de interesse (Fig. 10-22) Ponce e Lugo (2001) usaram análise de sensibilidade para mostrar que a extensão artificial do canal por uma quantidade igual ao comprimento do canal (ou seja, dobrando o comprimento do canal) pode ser suficiente para produzir uma curva precisa do loop na seção de interesse.

Extensão artificial do domínio computational usada em modelos de ondas dinâmicas mistas para especificar o contorno da montante

Fig. 10-22 Extensão artificial do domínio computational usada em modelos de ondas
dinâmicas mistas para especificar o contorno da montante.

QUESTÕES

[Problemas]   [Referências]   •   [Topo]   [Equações Governantes]   [Solução Linear]   [Ondas Cinemáticas]   [Ondas Difusivas]   [Método de Muskingum]   [Método de Muskingum-Cunge]   [Ondas Dinâmicas]

Quais leis de conservação são usadas na descrição de fluxo constante e gradualmente variado?
Quais leis de conservação são usadas na descrição do fluxo instável e gradualmente variado?
Quais forças estão atuando em um volume de controle em fluxo instável e gradualmente variado?
Quais tipos de ondas são comuns no fluxo instável de canais?
A que problemas as ondas cinemáticas se aplicam?
A quais problemas as ondas de difusão se aplicam?
Como é definido o L_o?
O que é número de onda adimensional?
Qual é a celeridade relativa adimensional das ondas cinemáticas sob atrito Chezy em canais hidraulicamente amplos?
Qual é a celeridade relativa adimensional das ondas dinâmicas sob atrito Chezy em canais hidraulicamente amplos?
Quais são as três maneiras de expressar a celeridade convectiva das ondas cinemáticas?
Qual é o número de Froude de estabilidade neutra para canais triangulares com atrito Chezy?
Qual é o número de Froude de estabilidade neutra para canais hidraulicamente amplos com atrito com Manning?
Qual é a base do método Muskingum-Cunge?
Qual é a contribuição da Hayami para o encaminhamento de inundações?
Para que valor do número de Vedernikov as difusividades hidráulicas cinemáticas e dinâmicas são as mesmas?
Para que valor do número de Vedernikov a difusividade hidráulica dinâmica desaparece?
Para que parte da propagação de inundação o parâmetro X de Muskingum é responsável?
O que é difusão numérica?
O que é dispersão numérica?
Qual é a vantagem do método Muskingum-Cunge?
Quando o método Muskigum-Cunge pode falhar em fornecer bons resultados?
Como o limite à jusante é especificado em um modelo dinâmico-cinemático misto, se desejarmos uma precisão maior?

PROBLEMAS

[Referências]   •   [Topo]   [Equações Governantes]   [Solução Linear]   [Ondas Cinemáticas]   [Ondas Difusivas]   [Método de Muskingum]   [Método de Muskingum-Cunge]   [Ondas Dinâmicas]   [Questões]

Você está observando a subida de um rio durante a enchente. A largura do rio no ponto de observação e a uma certa distância a montante é de 65 m, e de acordo com a leitura do medidor, a vazão é Q = 70 m³/s. Estime a descarga em um ponto localizado a 15.875 km à montante, se a superfície da água estiver subindo à taxa de 9 mm/h na sua localização e a 12 mm/h na seção transversal à montante.
Um canal hidraulicamente amplo está operando no número Froude F = 0,22. A vazão na largura da unidade é q = 2,8 m²/s. Quais são as duas celeridades Lagrange absolutas?
Uma onda de inundação está viajando na margem através de um alcance reto do rio com largura de topo T = 320 m e comprimento L = 5625 m. Para cada 1 cm de aumento de inundação, a descarga aumenta 10 m³/s. Quanto tempo leva para uma determinada descarga percorrer o comprimento do alcance?
Calcule o expoente β da curva-chave para um canal triangular com atrito Chezy.

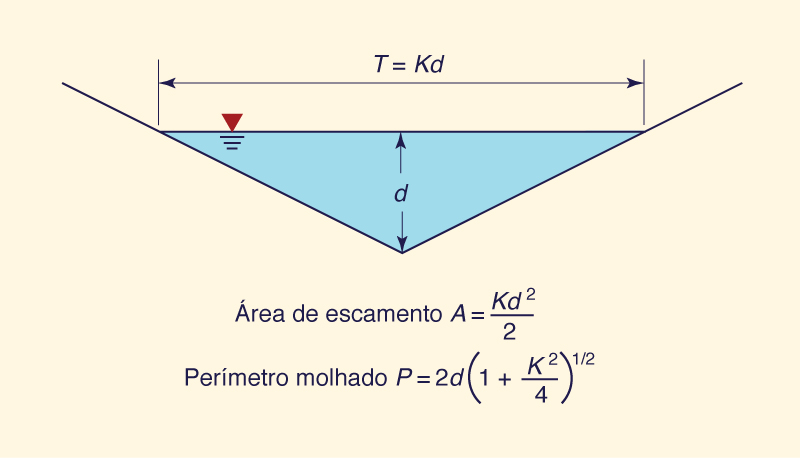
Desenho esquemático para um canal triangular

Fig. 10-23 Desenho esquemático para um canal triangular.

Calcule o expoente β da curva-chave para um canal triangular com atrito de Manning.
Um hidrograma de inundação tem os seguintes dados: Tempo-de-aumento t_r = 2 h, velocidade de referênciaV_o = 2 pés/s, profundidade de fluxo de referência d_o = 6 pés, declividade do leito S_o = 0,004. Determine se essa onda é uma onda cinemática.
Um hidrograma de inundação tem os seguintes dados: Tempo-de-aumento t_r = 2 h, velocidade de referênciaV_o = 2 pés/s, profundidade de fluxo de referência d_o = 6 pés, declividade do leito S_o = 0,004. Determine se essa onda é uma onda de difusão.
Um hidrograma de inundação tem os seguintes dados: Tempo-de-aumento t_r = 1 h, velocidade de referênciaV_o = 2 m/s, profundidade de fluxo de referência d_o = 2m, declividade do leito S_o = 0,004. Determine se essa onda é uma onda de difusão.
Usando o ONLINE ROUTING 04, direcione uma onda de inundação usando o método Muskingum. As ordenadas do hidrograma de entrada são [25 ordenadas, começando no tempo = 0, no tempo = 24 h:
100, 130, 150, 180, 220, 250, 300, 360, 450, 550, 700, 550, 490, 370, 330, 310, 280, 230, 170, 150, 130, 120, 110, 105, 100.
Suponha Δt = 1 h, K = 1 h, X = 0,3. Relate o pico de vazão e a hora da ocorrência.

Usando ONLINE ROUTING 05, propague a onda de inundação como no problema anterior usando o método Muskingum-Cunge. Utilizar os seguintes dados de entrada: Q_p = 700 m³/s, A_p = 400 m², T_p = 88 m, Δt = 1 h, Δx = 9,6 km, β = 1,65, S_o = 0,0007. Relate o pico de vazão e a hora da ocorrência.

REFERÊNCIAS

•   [Topo]   [Equações Governantes]   [Solução Linear]   [Ondas Cinemáticas]   [Ondas Difusivas]   [Método de Muskingum]   [Método de Muskingum-Cunge]   [Ondas Dinâmicas]   [Questões]   [Problemas]

Abbott, M. A. 1976. Computational hydraulics: A short pathology. Journal of Hydraulic Research, Vol. 14, No. 4, p. 276.
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York.
Craya, A. 1952. The criterion for the possibility of roll-wave formation. Gravity Waves, Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.
Cunge, J. A. (1969). On the Subject of a Flood Propagation Computation Method (Método de Muskingum), Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
Dooge, J . C. I. 1973. Linear theory of hydrologic systems. Technical Bulletin No. 1468, U.S. Department of Agriculture, Washington, D.C.
Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.
Kibler, D. F., e D. A. Woolhiser. 1970. The kinematic cascade as a hydrologic model. Hydrology Paper No. 39, Colorado State University, Ft. Collins, Colorado.
Kleitz, M. 1877. Note sur la théorie du mouvement non permanent des liquides et sur application à la propagation des crues des rivières, (Note on the theory of unsteady flow of liquids e on application to flood propagation in rivers), Annals des Ponts et Chaussées, ser. 5, Vol. 16, 2e semestre, 133-196.
Liggett, J. A. 1975. Basic equations of unsteady flow. Chapter 2 in Unsteady flow in open channels, K. Mahmood e V. Yevjevich, eds., Water Resources Publications, Ft. Collins, Colorado.
Liggett, J. A., e J. A. Cunge. 1975. Numerical methods of solution of the unsteady flow equations. Chapter 4 In Unsteady flow in open channels, K. Mahmood e V. Yevjevich, eds., Water Resources Publications, Ft. Collins, Colorado.
Lighthill, M. J., e G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
McCarthy, G. T. (1938). "The Unit Hydrograph e Flood Routing," unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, June 24.
Ponce, V, M., e D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.
Ponce, V. M., e V. Yevjevich. 1978. Muskingum-Cunge method with variable parameters. Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, December, 1663-1667.
Ponce, V. M., e F. D. Theurer. 1982. Accuracy criteria in diffusion routing. Journal of the Hydraulics Division, ASCE, Vol. 108, No. HY6, June, 747-757.
Ponce, V, M., e D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 4, April, 600-611.
Ponce, V. M. 1989. Engineering hydrology: Principles e practices. Prentice Hall, Englewood Cliffs, New Jersey.
Ponce, V. M. 1990. Generalized diffusion wave equation with inertial effects. Water Resources Research, Vol. 26, No. 5, May, 1099-1101.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.
Ponce, V, M., e P. J. Porras. 1995. Effect of cross-sectional shape of free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, April, 376-380.
Ponce, V, M., e A. Lugo. 2001. Modeling looped ratings in Muskingum-Cunge routing. Journal of Hydrologic Engineering, ASCE, Vol. 6, No. 2, March-April, 119-124.
Saint-Venant, B. de. 1871. Theorie du mouvement non-permanent des eaux avec application aux crues des rivieres et l' introduction des varees dans leur lit, Competes Rendus Hebdomadaires des Seances de l'Academie des Science, Paris, France, Vol. 73, 1871, 148-154.
Seddon, J. A. 1900. River hydraulics. Transactions, ASCE, Vol. XLIII, 179-243, June.
U.S. Army Corps of Engineers. 2020. River Analysis System: HEC-RAS, Version 5.0.7, Hydrologic Engineering Center, Davis, California.

http://hidraulicadecanaisabertos.sdsu.edu

200622 13:45

A visualização de documentos em PDF requer Adobe Acrobat Reader 5.0 ou versão mais atual; faça o download do Adobe Acrobat Reader.