|
|
|
CAPÍTULO 13: SEDIMENTOS EN EL CICLO HIDROLÓGICO |
|
"If a large dam is constructed on an alluvial-bed river, all of the sediment normally transported will be trapped. The clear water released will tend to erode the channel bed downstream from the dam until a new equilibrium is established." Hans A. Einstein (1950) |
|
"Si se construye una presa grande sobre un río de lecho aluvial, todo el sedimento que normalmente se transporta quedará atrapado. El agua liberada tenderá a erosionar el lecho del canal aguas abajo de la presa hasta que se establezca nuevamente el equilibrio". Hans A. Einstein (1950) |
|
This chapter is divided into five sections. Section 15.1 describes sediment properties; Section 15.2 describes sediment production, sediment sources, and sediment yield; Section 15.3 discusses sediment transport, sediment transport formulas, and sediment rating curves, including a brief introduction to sediment routing; Section 15.4 describes sediment deposition in reservoirs; and Section 15.5 describes sediment measurement techniques.
Este capítulo se divide en cinco secciones.
La Sección 13.1 describe las propiedades de los sedimentos.
La Sección 13.2 describe la producción, fuentes, y entrega de sedimentos.
|
13.1 PROPIEDADES DE LOS SEDIMENTOS
|
|
Rainfall and surface runoff are the agents responsible for the detachment and movement of soil particles on the land surface. These soil particles are referred to as sediments. The study of sediment detachment and movement is an important subject in engineering hydrology. Indeed, the subject of sediment transcends engineering hydrology to encompass the related fields of fluvial geomorphology, sediment transport, and sedimentation and river engineering [2, 4, 25, 40].
La lluvia y la escorrentía superficial son los agentes responsables del desprendimiento y movimiento de partículas de suelo en la superficie de la Tierra. Estas partículas del suelo se conocen como sedimentos. El estudio del desprendimiento y movimiento de sedimentos es un tema importante en la ingeniería hidráulica. De hecho, el tema de sedimentos trasciende la hidrología de ingeniería para abarcar los campos relacionados de geomorfología, transporte de sedimentos y sedimentación e ingeniería fluvial [2, 4, 25, 40].
The study of sediments in the hydrologic cycle can be divided into the following three processes: (1) production, (2) transport, and (3) deposition. These can be linked to the various liquid-transport phases of the hydrologic cycle. At the catchment level, sediment production by soil particle detachment is primarily the result of raindrop impact. Once detachment has taken place, surface runoff acts to transport sediment downslope, first as overland flow (sheet and rill flow), and eventually as stream and river flow. Deposition of sediment occurs at any point downstream where the kinetic energy of the flow is insufficient to support sediment entrainment in the flowing water.
El estudio de los sedimentos en el ciclo hidrológico se puede dividir en los siguientes tres procesos:
- Producción,
- Transporte y,
- Deposición.
Estos procesos pueden estar vinculados a las diversas fases de transporte de líquidos del ciclo hidrológico. A nivel de cuenca, la producción de sedimentos es el resultado del desprendimiento de partículas del suelo, principalmente por el impacto de las gotas de lluvia. Una vez que el desprendimiento ha tenido lugar, la escorrentía superficial actúa para transportar el sedimento por la pendiente descendente, primero como flujo superficial (flujo de lámina y arroyuelo), y finalmente como corriente y flujo de río. La deposición de sedimentos ocurre en cualquier punto aguas abajo donde la energía cinética del flujo es insuficiente para soportar el arrastre de sedimentos en el agua que fluye.
Sediment production refers to the processes by which sediment is produced, the identification of sediment sources and amounts, and the determination of sediment yields. The source of sediment can usually be traced back to the upland catchments, although these are by no means the only source. In certain cases, streambank erosion in the lower valleys may constitute an important source of sediment.
La producción de sedimentos se refiere a los procesos por los cuales éstos son producidos, la identificación de las fuentes y cantidades de sedimentos, y la determinación de los rendimientos. La fuente del sedimento generalmente se puede remontar a las cuencas de las tierras altas, aunque de ninguna manera son la única fuente. En ciertos casos, la erosión de los bancos de arena en los valles inferiores pueden constituir una importante fuente de sedimentos.
Sediment from upland catchments is delivered to streams and rivers, wherein sediment transport takes place. Sediment transport refers to the mechanisms by which sediment is moved downstream by flowing water, either in suspension or by rolling and sliding along the river bottom.
Los sedimentos de las cuencas altas son liberados a los arroyos y ríos, y es aquí donde el transporte de sedimentos toma lugar. El transporte de sedimentos se refiere a los mecanismos por los cuales los sedimentos se mueven aguas abajo a través del agua que fluye, ya sea suspendidos, por rodamiento, o por deslizamiento a lo largo del fondo del río.
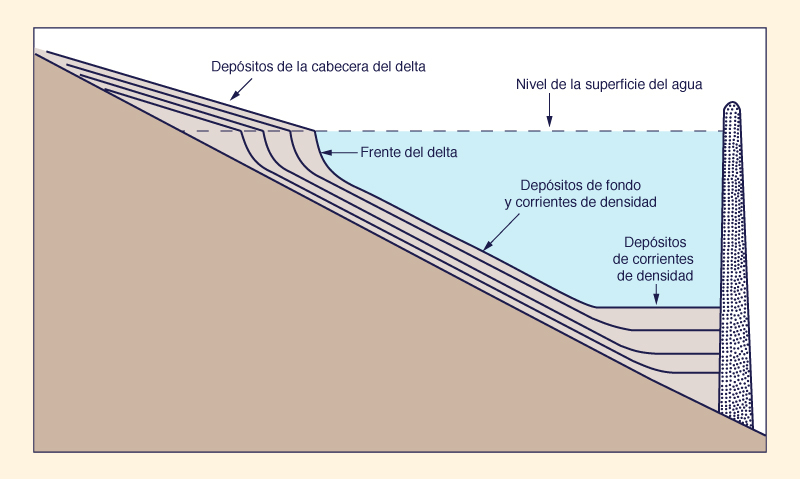
The transport of sediment continues in the downstream direction until the flow is no longer able to carry the sediment, at which time sediment deposition occurs. Typically, the first opportunity for sediment deposition is at the entrance to reservoirs and water impoundments, where the flow is decelerated by the action of structures. Deposition is also likely to occur naturally, for instance, downstream of sudden decreases in energy slope or in situations where the capacity of the flow to carry sediment is substantially diminished. In the absence of these natural or human-made features, sediment transport by the flow may continue unabated until it reaches the estuary or ocean, at which time the flow loses its kinetic energy and sediment deposition goes on to contribute to delta growth.
El transporte de sedimentos continúa aguas abajo hasta que el flujo ya no es capaz de transortar el sedimento; es aquí donde se produce la deposición de sedimentos. Típicamente, la primera oportunidad para la deposición de sedimentos está en la entrada a los depósitos y embalses de agua, donde el flujo se desacelera por la acción de las estructuras. También es probable que la deposición se produzca de forma natural; por ejemplo, aguas abajo, por la disminución repentina en la pendiente de energía o en situaciones en las que la capacidad del flujo para transportar los sedimentos se encuentra considerablemente disminuida. En ausencia de estas características naturales ó aquéllas hechas por el hombre, el transporte de sedimentos a través del flujo puede continuar sin cesar hasta llegar a un estuario ó al oceáno, momento en el cual el flujo pierde su energía cinética y la deposición de sedimentos sirve para contribuir al crecimiento del delta.
Formación de Sedimentos
Sediments are the products of disintegration and decomposition of rocks. Disintegration includes all processes by which rocks are broken into smaller pieces without substantial chemical change. The disintegration of rocks is caused either by large temperature changes or by alternate cycles of freezing and thawing. Decomposition refers to the breaking down of mineral components of rocks by chemical reaction. Decomposition includes the follwing processes: (1) carbonation, (2) hydration, (3) oxidation, and (4) solution.
Los sedimentos son el producto de la desintegración y la descomposición de las rocas. La desintegración incluye todos los procesos por los que las rocas se rompen en pedazos más pequeños sin un cambio químico sustancial. La desintegración es causada ya sea por grandes cambios de temperatura, ó por ciclos alternos de congelación y descongelación. La descomposición se refiere a la ruptura de los componentes minerales de las rocas por reacción química, e incluye los procesos siguientes: (1) Carbonatación, (2) Hidratación, (3) Oxidación, y (4) Solución.
Carbon dioxide (CO2), present in the atmosphere and organic sources, readily unites with water to form carbonic acid (H2CO3). Carbonic acid reacts with feldspars to produce clay minerals, silica, calcite, and other relatively soluble carbonates containing potassium, sodium, iron, and magnesium. The addition of water to many of the minerals present in igneous rocks results in the formation of clay minerals such as aluminum silicates. Many secondary minerals are formed from igneous rocks by oxidation, which is accelerated by the presence of moisture in the air. Solution is another important mechanism in the alteration of igneous rock. Oxygen combines with other elements to form sulfates, carbonates, and nitrates, most of which are relatively soluble. The amount (by weight) of dissolved solids carried by streams in the contiguous United States has been estimated at more than 50 percent of the amount of suspended sediment [32].
El dióxido de carbono (CO2, presente en la atmósfera y fuentes orgánicas, se une fácilmente con el agua para formar ácido carbónico (H2CO3). El ácido carbónico reacciona con los feldespatos para producir minerales de arcilla, sílice, calcita y otros carbonatos relativamente solubles que contienen potasio, sodio, hierro y magnesio. La adición de agua a muchos de los minerales presentes en las rocas ígneas da como resultado la formación de minerales de arcilla tales como silicatos de aluminio. Muchos minerales secundarios se forman a partir de las rocas ígneas por oxidación, la cual se acelera por la presencia de humedad en el aire. La solution es otro mecanismo importante en la alteración de la roca ígnea. El oxígeno se combina con otros elementos para formar sulfatos, carbonatos y nitratos, la mayoría de los cuales son relativamente solubles. La cantidad (en peso) de sólidos disueltos llevadas por las corrientes en los estados contiguos de los Estados Unidos se ha estimado en más de 50 por ciento de la cantidad de sedimentos suspendidos [32].
Características de las Partículas
The characteristics of mineral grains help describe the properties of sediments. Among them are: (1) size, (2) shape, (3) specific weight and specific gravity, and (4) fall velocity.
Las características de los granos minerales ayudan a describir las propiedades de los sedimentos. Entre ellos se encuentran: (1) tamaño, (2) forma, (3) peso específico y gravedad específica, y (4) velocidad de caída.
Size. Particle size is a readily measured sediment characteristic. A widely accepted classification of sediments according to size is shown in Table 15-1. Five groups of sizes are included in this table: (1) boulders and cobbles, (2) gravel, (3) sand, (4) silt, and (5) clay. Boulders and cobbles can be measured individually. Gravel-size particles can be measured individually or by sieving. Sand-size particles are readily measured by sieving. A No. 200 screen is used to separate sand particles from finer particles such as silt and clay. Silt and clay particles are separated by measuring the differences in their rate of fall in still water.
Tamaño. El tamaño de partícula es una característica fácilmente medible de los sedimentos.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Shape. Particle shape is numerically defined in terms of its sphericity and roundness. True sphericity is the ratio of the surface area of a sphere having the same volume as the particle to the surface area of the particle. The practical difficulty of measuring true sphericity has led to an alternate definition of sphericity as the ratio of the diameter of a sphere having the same volume as the particle (i.e., the nominal diameter) to the diameter of a sphere circumscribing the particle. Accordingly, a sphere has a sphericity of 1, whereas all other shapes have a sphericity of less than 1.
Forma. La forma de la partícula se define numéricamente en términos de su esfericidad y redondez. La verdadera esfericidad es la relación entre la superficie de una esfera que tiene el mismo volumen que la partícula, y la superficie de la partícula. La dificultad práctica de medir la esfericidad verdadera ha llevado a una definición alternativa de esfericidad como la relación del diámetro de una esfera que tiene el mismo volumen que la partícula (es decir, el diámetro nominal) con el diámetro de una esfera que circunscribe a la partícula. En consecuencia, una esfera tiene una esfericidad de 1, mientras que todas las otras formas tienen una esfericidad de menos de 1.
Roundness is defined as the ratio of the average radius of curvature of the particle edges to the radius of the largest inscribed circle. It refers to the sharpness of the edges of sediment particles and is commonly used as an indicator of particle wear.
La redondez se define como la relación entre el radio de curvatura promedio de los bordes de la partícula y el radio del círculo inscrito más grande. Se refiere a la nitidez de los bordes de las partículas de sedimentos y se usa comúnmente como indicador de desgaste de partículas.
In sediment studies, the shape factor is often used as an indicator of particle shape:
En el estudio de sedimentos, el factor de forma se utiliza normalmente como un indicador de la forma de las partículas:
|
c
FF = ________ (ab)1/2 | (13-1) |
in which SF = shape factor and a, b, and c are three orthogonal particle length dimensions. According to Corey [12], a is the longest, b is the intermediate, and c is the shortest length dimension. However, according to McNown and Malaika [34], c is measured in the direction of motion, and a and b are perpendicular to c.
en la cual FF = factor de forma y a, b, y c son tres longitudes ortogonales de partículas. Según Corey [12], a es la más larga, b es la intermedia, y c es la longitud más corta. Sin embargo, de acuerdo con McNown y Malaika [34], c se mide en la dirección del movimiento, y a y b son perpendiculares a c .
Specific Weight and Specific Gravity. The specific weight of a sediment particle is its weight per unit volume. The specific gravity of a sediment particle is the ratio of its weight to the weight of an equal volume of water. Most sediment particles consist of either quartz or feldspar, which are about 2.65 times heavier than water. Therefore, the specific gravity of sediments is generally considered to be about 2.65. Exceptions are heavy minerals (for instance, magnetite, with specific gravity of 5.18), but these occur rather infrequently.
Peso específico y gravedad específica . El peso específico de una partícula de sedimento es la relación de su peso por unidad de volumen. La gravedad específica de una partícula de sedimento es la relación de su peso al peso de un volumen igual de agua. La mayoría de las partículas de sedimento consisten ya sea de cuarzo o feldespato, los cuales son alrededor de 2,65 veces más pesados que el agua. Por lo tanto, la gravedad específica de los sedimentos se considera generalmente igual a 2,65. Las excepciones son minerales pesados (por ejemplo, la magnetita, con peso específico de 5,18), pero estos ocurren con muy poca frecuencia.
Fall Velocity. The fall velocity of a sediment particle is its terminal rate of settling in still water. Fall velocity is a function of size, shape, and specific weight of the particle, and the specific weight and viscosity of the surrounding water. For spherical particles, the fall velocity (derived from a balance of submerged weight and drag) can be expressed as follows:
Velocidad de caída. La velocidad de caída de una partícula de sedimento es su tasa de asentamiento en agua inmóvil. La velocidad de caída es una función del tamaño, forma y el peso específico de la partícula, y del peso específico y viscosidad del agua circundante. Para partículas esféricas, la velocidad de caída (derivada de un equilibrio de peso sumergido y la fricción actuante) se puede expresar de la siguiente manera:
|
4 g ds γs - γ
w = [ ___ ______ ________ ] 1/2 3 CD γ | (13-2) |
in which w = fall velocity, g = gravitational acceleration, ds = particle diameter, CD = drag coefficient (dimensionless), γs = specific weight of sediment particles, and γ = specific weight of water.
en la cual:
w = velocidad de caída;
g = aceleración de la gravedad;
d s = diámetro de la partícula;
The drag coefficient is a function of the particle Reynolds number R, defined as follows:
El coeficiente de arrastre es función del número de Reynolds de la partícula R, definido como sigue:
|
w ds
R = ______ ν | (13-3) |
in which ν = kinematic viscosity of the fluid. For particle Reynolds numbers less than 0.1, the drag coefficient is equal to CD = 24/R. Substituting this value of CD into Eq. 15-2 leads to Stokes' law:
en el cual ν = viscosidad cinemática del fluido. Para números de Reynolds de partícula menores de 0,1, el coeficiente de arrastre es igual a CD = 24/R. Sustituyendo este valor de CD en la Ec. 15-2 lleva a la ley de Stokes:
|
g d 2 γs - γ
w = [ _______ ] ( ________ ) 18 ν γ | (13-4) |
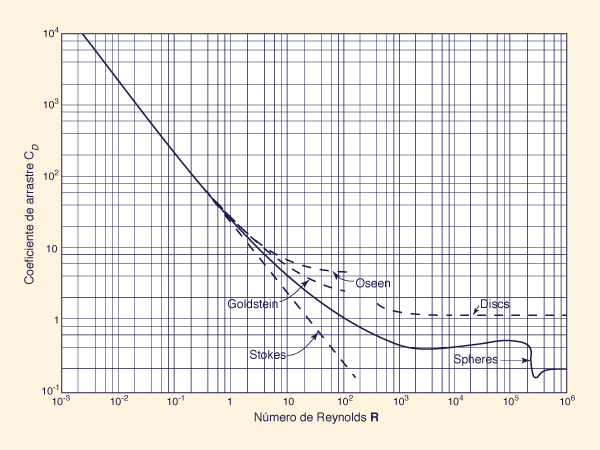
For particle Reynolds numbers greater than 0.1, the drag coefficient is still a function of Reynolds number, but the relationship cannot be expressed in analytical form. The relationship of CD versus R for a wide range of particle Reynolds numbers is shown in Fig. 15-1 [38].
Para números de Reynolds de partícula mayores de 0.1, el coeficiente de arrastre sigue siendo una función del número de Reynolds, pero la relación no puede expresarse en forma analítica. La Figura 13-1 muestra la relación CD vs R para un rango amplio de números de Reynolds de partícula [38].
Figura 13-1 Coeficiente de arrastre vs número de Reynolds de la partícula [38]. |
Ejemplo 13-1.
Calcular la velocidad de caída de una partícula
esférica de cuarzo de diámetro ds = 0,1 mm y
coeficiente de arrastre C D = 40.
Usando la Ec. 13-2, con γs = 2,65 g/cm3,
γ = 1 g/cm3,
g = 9,81 m/s2, y ds = 0,0001 m, la velocidad de caída es:
|
Frecuentemente el coeficiente de arrastre no se
conoce a priori;
en este caso, se justifica una solución iterativa.
Se asume un número de Reynolds de la partícula, y el coeficiente de arrastre se obtiene de la
Ejemplo 13-2.
Calcular la velocidad de caída de una partícula esférica de cuarzo,
de diámetro
ds = 0,1 mm, y
la temperatura del agua
Establecer un procedimiento iterativo utilizando los siguientes pasos:
Empleando ENLINEA VELOCIDAD CAIDA,
la respuesta, después de 12 iteraciones, es: |
Standard fall velocity. Since fall velocities vary with fluid temperature and viscosity, two particles of the same size, shape, and specific gravity, falling on two fluids of different viscosity, or in the same fluid at different temperatures, will have different fall velocities. To provide a measure of comparison, the concept of standard fall velocity was developed [23]. The standard fall velocity of a particle is the average rate of fall that it would attain if falling alone in quiescent water of infinite extent at the temperature of 24°C. Likewise, the standard fall diameter of a particle is the diameter of an equivalent sphere having the same standard fall velocity and specific gravity.
Velocidad de caída estándar. Dado que las velocidades de caída varían con la temperatura y viscosidad del fluido, dos partículas del mismo tamaño, forma y gravedad específica, las cuales caen en dos fluidos de diferente viscosidad, o en el mismo fluido a diferentes temperaturas, tendrán distintas velocidades de caída. Con el fin de proporcionar una medida de comparación, se ha desarrollado el concepto de velocidad de caída estándar [23]. La velocidad de caída estándar de una partícula es la velocidad media de caída que alcanzaría si cae en agua en reposo de extensión infinita a una temperatura de 24°C. De la misma manera, el diámetro de una partícula de caída estándar es el de una esfera equivalente con la misma velocidad de caída estándar y gravedad específica.
Distribución del tamaño de los depósitos de sedimentos
An important property of sediment deposits is the size distribution of its individual particles. Particle size distribution is a key to predicting the behavior of a sediment deposit and estimating its specific weight. A sediment sample containing a wide range of particle sizes is well graded, or poorly sorted. Conversely, a sediment sample consisting of particles in a narrow range of particle sizes is poorly graded, or well sorted.
Una propiedad importante de los depósitos de sedimentos es la distribución del tamaño de partículas, la cual es clave para predecir el comportamiento de un depósito de sedimentos y estimar su peso específico. Una muestra de sedimento que contiene un amplio rango de tamaños de partículas está bien graduada o mal seleccionada. Por el contrario, una muestra de sedimento que consta de partículas en un rango estrecho de tamaños está mal graduada o bien seleccionada.
The size distribution of sediments can be measured in several ways. The coarsest fraction can be separated by direct measurement for boulders and cobbles and by sieving for sands and gravels. For most applications involving sediments in the sand size, the visual accumulation (VA) tube is a fast, economical, and accurate method of determining the size distribution of sediment samples. In the VA tube method, the particles start falling from a common source and become stratified according to their relative settling velocities. At a given instant, the particles coming to rest at the bottom of the tube are of a certain sedimentation size, finer than particles that have already settled and coarser than those still remaining in suspension. See [19] for a description of laboratory methods for sediment analysis.
La distribución del tamaño de sedimentos se puede medir de varias maneras. La fracción más gruesa se puede separar por medición directa de cantos rodados y adoquines, y tamizando la arena y grava. Para la mayoría de las aplicaciones que involucran sedimentos en el tamaño de arena, el tubo de acumulación visual (AV) es un método rápido, económico y preciso para determinar la distribución del tamaño de sedimentos. En el método del tubo AV, las partículas comienzan a caer desde una fuente común y se estratifican de acuerdo con sus velocidades relativas de sedimentación. En un instante dado, las partículas que se detienen en el fondo del tubo tienen un cierto tamaño de sedimentación, más fino que las partículas que ya se han asentado y más grueso de las que aún permanecen en suspensión. Ver [19] para una descripción de los métodos de laboratorio para análisis de sedimentos.
Peso específico de los depósitos de sedimentos
The specific weight of a sediment deposit is the dry weight of sedimentary material per unit volume. Due to the voids between sediment particles, the specific weight of a sediment deposit is always less than the specific weight of individual particles. A knowledge of the specific weight of a sediment deposit allows the conversion of sediment weights to sediment volumes and vice versa. In particular, the specific weight of a sediment deposit is useful in studies of reservoir storage depletion by deposition of fluvial sediments.
El peso específico de un depósito de sedimentos es el peso seco del material sedimentado, por unidad de volumen. Debido a los vacíos entre las partículas sedimentadas, el peso específico de un depósito es siempre menor que el peso específico de las partículas (individuales). El conocimiento del peso específico de un depósito de sedimentos permite la conversión de pesos a volúmenes de sedimentos, y viceversa. En particular, el peso específico de un depósito es útil en los estudios de pérdida del volumen de almacenamiento de embalses por deposición de sedimentos fluviales.
Factors influencing the specific weight of a sediment deposit are: (1) its mechanical composition, (2) the environment in which the deposits are formed, and (3) time. Coarse materials, e.g., boulders, gravel, and coarse sand, are deposited with specific weights very nearly equal to their ultimate value and change very little with time. However, fine materials such as silts and clays may have initial specific weights that are only a fraction of their ultimate value.
Los factores que influyen en el peso específico de un depósito de sedimentos son:
Lane and Koelzer [29] have developed an empirical relationship to account for the variation of the specific weight of sediment deposits in reservoirs with time. Their relationship is:
Lane y Koelzer [29] han desarrollado una relación empírica para tomar en cuenta la variación del peso específico de los depósitos de sedimentos en reservorios con el tiempo. Esta relación es:
| W = W1 + B log T | (13-5) |
in which W = specific weight of the deposit after T years; W1 = initial specific weight of the deposit, measured after 1 y of consolidation; and B = a constant. Table 15-2 shows values of W1 and B as a function of sediment size and mode of reservoir operation. For mixed deposits, a weighted average of specific weight is appropriate.
en la cual W = peso específico del depósito después de T años; W1 = peso específico inicial del depósito, medido después de un (1) año de consolidación; y B = una constante. La Tabla 13-2 muestra los valores de W1 y B en función del tamaño de los sedimentos y el modo de operación del embalse. Para los depósitos mixtos, se puede tomar un valor de la media ponderada.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Drying or aeration of a sediment deposit helps to accelerate consolidation through removal of the water from the pore spaces. Table 15-3 shows the effect of aeration on the specific weight of sediment deposits for several types of soil mixtures [18].
El secado o la aireación de un depósito de sedimentos ayuda a acelerar la consolidación a través de la eliminación del agua de los poros. La Tabla 13-3 muestra el efecto de la aireación en el peso específico de los depósitos de sedimentos, para varios tipos de mezclas de suelo [18].
| |||||||||||||||||||||||||||||||||
Ejemplo 13-3.
Calcular el peso específico de un depósito de sedimentos
en un embalse después de un tiempo transcurrido de 50 años.
Considerar el sedimento siempre sumergido o casi sumergido.
Suponer la siguiente distribución de tamaños de granos: arena, 30%; limo, 45%; y arcilla, 25%.
Usando la Tabla 13-2, los pesos específicos para los distintos tamaños son:
arena, 93 libras/pie3; limo, 74,7 lb/pie3; y
arcilla,
Usando ENLINEA LANE KOELZER,
la respuesta es: Peso específico total = 75,8 lb/pie3.
|
13.2 PRODUCCIÓN DE SEDIMENTOS
|
|
The presence of sediment in streams and rivers has its origin in soil erosion. Erosion encompasses a series of complex and interrelated natural processes that have the effect of loosening and moving away soil and rock materials under the action of water, wind, and other geologic factors. In the long term, the effect of erosion is the denudation of the land surface, i.e., the removal of soil and rock particles from exposed surfaces, their transport to lower elevations, and eventual deposition.
La presencia de sedimentos en arroyos y ríos tiene su origen en la erosión. La erosión abarca una serie de procesos naturales interrelacionados, que tienen el efecto de aflojar y mover el suelo y materiales rocosos bajo la acción del agua, el viento y otros factores geológicos. A largo plazo, el efecto de la erosión es la denudación de la superficie de la Tierra, es decir, la remoción del suelo y las partículas de roca expuestas, su transporte a elevaciones más bajas y su eventual deposición.
The rate of landscape denudation can be quantified from a geological perspective. For instance, the number of centimeters of denudation per 1000 y can be used as a measure of the erosive activity of a region. Geologic measures of landscape denudation appear insignificant when compared to the typical timespan of human activity, say 25 to 100 y. However, the quantities of sediment moved may be important when considering the impact that sediment loads have on the operation and design life of reservoirs and hydraulic structures.
La velocidad de denudación del paisaje se puede cuantificar desde una perspectiva geológica.
At the outset of the study of sediment production, a distinction should be made between the amount of sediment eroded at the source(s) and the amount of sediment delivered to a downstream point. Gross sediment production refers to the amount of sediment eroded and removed from the source(s). Sediment yield refers to the actual delivery of eroded soil particles to a given downstream point. Since eroded particles may be deposited before they reach the downstream point of interest, sediment yield quantities are generally less than gross sediment production quantities. The ratio of sediment yield to gross sediment production is the sediment delivery ratio (SDR).
Al comienzo del estudio de producción de sedimentos, debe hacerse una distinción entre la cantidad de sedimentos
erosionados en la(s) fuente(s) y la cantidad de sedimento entregado a un punto localizado aguas abajo.
La producción bruta de sedimentos se refiere a la cantidad de sedimento erosionado y eliminado de la(s) fuente(s).
El rendimiento de sedimentos se refiere a la entrega actual de partículas erosionadas a un punto de interés,
localizado aguas
abajo. Dado que las partículas erosionadas pueden depositarse antes de que lleguen al punto de interés aguas
abajo, el rendimiento de sedimentos es generalmente inferior a la de producción de sedimento bruto.
Gross sediment production is commonly measured in terms of weight of sediment per unit drainage area per unit time-for instance, metric tons per hectare per year, or tons per acre per year. Sediment yield is expressed in terms of weight per unit time past a certain point; for instance, metric tons per day at the catchment outlet.
La producción bruta de sedimentos se mide comúnmente en términos del peso del sedimento por unidad de área de drenaje por unidad de tiempo; por ejemplo, en toneladas métricas por hectárea por año, o toneladas por acre por año. El rendimiento de sedimentos se expresa en términos de peso por unidad de tiempo en cierto punto; por ejemplo, toneladas métricas por día en la boca de la cuenca.
Erosión Normal y Acelerada
According to the timespan involved, erosion may be classified as: (1) normal, or geologic, and (2) accelerated, or human-induced. Normal erosion has been occurring at variable rates since the first solid materials formed on the surface of the earth. Normal erosion is extremely slow in most places and is largely a function of climate, parent rocks, precipitation, topography, and vegetative cover. Accelerated erosion occurs at a much faster rate than normal, usually through reduction of vegetative cover. Deforestation, overgrazing, overcultivation, urban sprawl, and the systematic destruction of natural vegetation result in accelerated erosion.
Según el intervalo de tiempo involucrado, la erosión se puede clasificar en: (1) normal, ó geológica, y (2) acelerada, o inducida por el hombre. La erosión normal se ha producido a tasas variables desde que se formaron los primeros materiales sólidos en la superficie de la Tierra. Aquélla es extremadamente lenta en la mayoría de los casos, y es en gran parte una función del clima, el tipo de roca madre, la precipitación, la topografía y la cubierta vegetal predominante. Por el contrario, la erosión acelerada ocurre a un ritmo mucho más rápido que el normal, generalmente a través de la reducción de la cubierta vegetal. La deforestación, el sobrepastoreo, el sobrecultivo, la expansión urbana, y la destrucción sistemática de vegetación natural usualmente resulta en erosión acelerada.
Fuentes de Sedimentos.
De acuerdo a la fuente, la erosión puede clasificarse en: (1) erosión de lámina, (2) erosión de canaletas,
(3) erosión de barrancas, y (4) erosión de canales.
La erosión de lámina es el desgaste de una capa delgada en la superficie de la Tierra, principalmente
causada por el flujo superficial.
Erosión de Cuenca de Cabecera y la Ecuación Universal de Pérdida de Suelo
In the United States, the prediction of upland erosion (i.e., sheet and rill erosion) is commonly made by the Universal Soil Loss Equation (USLE), developed by the USDA Agricultural Research Service in cooperation with the USDA Soil Conservation Service (now Natural Resources Conservation Service) and certain state experiment stations.
En los Estados Unidos, la predicción de la erosión de superficie en la cabecera de cuenca se realiza comúnmente con la Ecuación Universal de Pérdida de Suelo, desarrollada por el Servicio de Investigación Agrícola, en cooperación con el Servicio de Conservación de Suelos y ciertas estaciones experimentales estatales.
The universal soil loss equation is [46]:
La Ecuación Universal de Pérdida de Suelo es la siguiente [46]:
| A = R K L S C P | (13-6) |
en la cual A = pérdida anual de suelo debido a la erosión de superficie, en toneladas por acre por año: R = factor de precipitación; K = factor de erodibilidad del suelo; L = factor de lengitud; S = factor de gradiente;; C = factor de manejo del cultivo; y p = factor de la práctica del control de erosión.
Rainfall Factor. When factors other than rainfall are held constant, soil losses from cultivated fields are shown to be directly proportional to the product of the storm's total kinetic energy E and its maximum 30-minute intensity I. The product EI reflects the combined potential of raindrop impact and runoff turbulence to transport dislodged soil particles.
Factor de precipitación. Cuando otros factores, aparte de la precipitación, se mantienen constantes, las pérdidas de suelo son directamente proporcionales al producto de la energía cinética total de la tormenta E y su máxima intensidad, de 30 minutos de duración I. El producto EI refleja el potencial combinado del impacto de la precipitación y de la turbulencia de la escorrentía para transportar las partículas de suelo desagregadas.
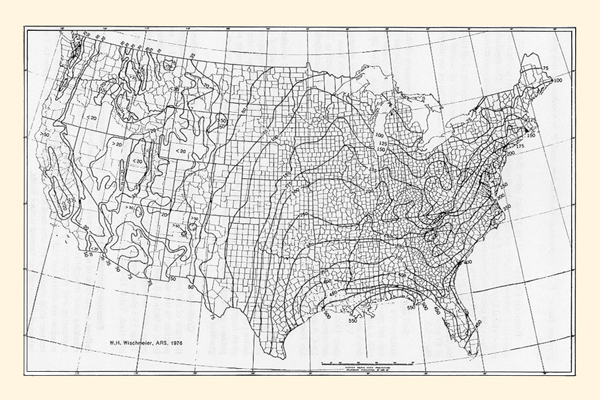
The sum of EI products for a given year is an index of the erosivity of all rainfall for that year. The rainfall factor R is the average value of the series of annual sums of EI products. Values of R applicable to the contiguous United States are shown in Fig. 15-2.
La suma del producto EI para un año determinado es el índice de erosión de todas las precipitaciones para ese año. El factor de precipitación R es el valor medio de la serie de sumas anuales del producto EI. La Figura 13-2 muestra los valores de R aplicables en el área contigua de los Estados Unidos.
Figura 15-2 Factor de precipitación R en la Ecuación Universal de Pérdida de Suelo [44]. |
Soil Erodibility Factor. The soil erodibility factor K is a measure of the resistance of a soil surface to erosion. It is defined as the amount of soil loss (in tons per acre per year) per unit of rainfall factor R from a unit plot. A unit plot is 72.6 ft long, with a uniform lengthwise gradient of 9 percent, in continuous fallow, tilled up and down the slope.
Factor de erodibilidad del suelo. El factor de erodibilidad del suelo K es una medida de la resistencia a la erosión de la superficie del suelo. Este factor se define como la cantidad de pérdida de suelo (en toneladas por acre al año), por unidad de factor de lluvia R, en una unidad de parcela. Una unidad de parcela mide 72.6 pies de largo, con un gradiente longitudinal uniforme del 9 por ciento, en barbecho continuo, labrado en dirección de la pendiente.
Values of K for 23 major soils on which erosion plot studies were conducted since 1930 are listed in Table 15-4. Soil erodibility factors for other soils have been estimated by comparing their characteristics with those of the 23 soils listed in Table 15-4. A method for determining the soil erodibility factor based on soil characteristics has been proposed by Wischmeier et al. [47].
La Tabla 13-4 lista los valores de K para los veintitrés (23) suelos principales en los cuales se han realizado estudios de erosión en parcela desde 1930. Los valores de K para otros suelos se han comparado con las características de los 23 suelos listados en esta tabla. Wischmeier y otros [47] han propuesto un método para determinar el factor de erosión en base a las características del suelo.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
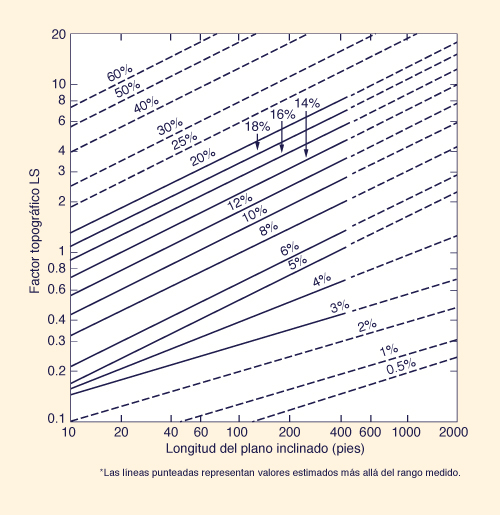
Slope-length and Slope-gradient Factors. The rate of soil erosion by flowing water is a function of slope length (L) and gradient (S). For practical purposes, these two topographic characteristics are combined into a single topographic factor (LS). The topographic factor is defined as the ratio of soil loss from a slope of given length and gradient to the soil loss from the unit plot (of 72.6 ft length and 9 percent gradient). Figure 15-3 shows values of LS as a function of slope length and gradient.
Factores de pendiente-longitud y pendiente-gradiente. La tasa de erosión hídrica del suelo es una función de la longitud de pendiente (L) y del gradiente (S). Para propósitos prácticos, estas dos características topográficas se combinan en un solo factor (LS), el cual se define como la relación de pérdida del suelo de una pendiente de longitud y gradiente dado, a la pérdida del suelo de una parcela unitaria, de 72,6 pies de longitud y 9 por ciento de gradiente. La Figura 13-3 muestra los valores de LS en función de la longitud de pendiente y el gradiente.
Figura 13-3 Factor Topográfico LS en la Ecuación Universal de Pérdida de Suelo [44]. |
Crop-management Factor. The crop-management factor C is defined as the ratio of soil loss from a certain combination of vegetative cover and management practice to the soil loss resulting from tilled, continuous fallow. Values of C range from as little as 0.0001 for undisturbed forest land to a maximum of 1.0 for disturbed areas with no vegetation. Values of C for cropland are estimated on a local basis. Table 15-5 shows values of C for permanent pasture, grazed forest land, range, and idle land. Table 15-6 shows values of C for undisturbed forest land.
Factor de manejo del cultivo. El factor de manejo del cultivo C se define como la relación entre la pérdida de suelo de una cierta combinación de cubierta vegetal y práctica de manejo, a la pérdida de suelo resultante de un barbecho continuo. El rango de valores de C varía desde pequeños valores de 0,0001 para tierras forestales inalteradas, hasta un máximo de 1.0 para áreas completamente alteradas, sin vegetación. Los valores de C para tierras de cultivo se estiman sobre una base local. La Tabla 13-5 muestra los valores de C para pastizales permanentes, tierras de pastoreo, pastos y tierras sin uso. La Tabla 13-6 muestra valores de C para áreas forestales no disturbadas.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||
Factor de práctica de control de erosión P . Este factor se define como la relación entre la pérdida de suelo bajo una determinada práctica de control de erosión y la pérdida de suelo resultante del cultivo en hileras. Las prácticas para las cuales los valores de P han sido establecidas son las de contorno y curva de contorno. En el cultivo de contorno, las tiras de césped o prado se alternan con franjas de cultivos en hileras o pequeños granos. Los valores de P empleados para cultivo de contornos también se utilizan para los cultivos de regadío con surcos de contorno. La Tabla 13-7 muestra los valores de P para campos de terrazas de cultivo de contorno.
| |||||||||||||||||||||||||||||||||||||||||||||||||
Use of the Universal Soil Loss Equation (USLE). The USLE computes upland erosion from small watersheds on an average annual basis. It includes the detachment and transport components, but it does not account for the deposition component. Therefore, the USLE cannot be used to compute sediment yield. For example, in a 1000-mi2 drainage basin, only 5 percent of the soil loss computed by the USLE may appear as sediment yield at the basin outlet. The remaining 95 percent is redistributed on uplands or flood plains and does not constitute a net soil loss from the drainage basin.
Uso de la Ecuación Universal de Pérdida de Suelo (EUPS). La EUPS calcula la erosión de tierras altas de pequeñas cuencas hidrográficas sobre una base anual promedio. Incluye los componentes de desprendimiento y transporte, pero no representa el componente de deposición. Por lo tanto, la EUPS no se puede usar para calcular el rendimiento de sedimentos. Por ejemplo, en una cuenca de 1000 km2, solo el 5% de la pérdida de suelo calculada por la EUPS puede aparecer como rendimiento de sedimento en la salida de la cuenca. El 95 por ciento restante se redistribuye en las tierras altas o llanuras de inundación y no constituye una pérdida neta de suelo de la cuenca de drenaje.
Ejemplo 13-4.
Asuma una estructura propuesta
de control de inundaciones en una cuenca hidrográfica de 600 acres en el condado
de Fountain, Indiana. Calcule la pérdida media anual de suelo por la ecuación universal de pérdida de suelo (EUPS)
para las
siguientes condiciones: (1) tierras de cultivo, 280 ac, contorno redondeado en tiras, el suelo es marga limosa Fayette,
las pendientes tienen un 8% y 200 pies de largo; (2) pastos, 170 ac, 50% de cobertura del dosel, 80% de cobertura del
suelo con pasto, suelo con limo franco de Fayette, pendientes de 8% y 200 pies de largo; y (3) bosque, 150 ac, el suelo
es marga limosa Marshall, 30% cubierta del dosel arbóreo, las pendientes son 12% y 100 pies de largo.
From Fig. 15-2: R = 185.
From Table 15-4, K = 0.38.
From Fig. 15-3, LS = 1.4.
The value of C for cropland is obtained from local sources; assume C = 0.12 for this
example.
From Table 15-7, R = 185; K = 0.38: LS = 1.4.
From Table 15-5, C = 0.012.
No value of P has been established for pasture; therefore, P = 1.
Using Eq. 15-6: A = 185 × 0.38 × 1.4 × 0.012 × 1.0 = 1.18 tons/ac/y.
R = 185.
From Table 15-4, K = 0.33.
From Fig. 15-3, LS = 1.8.
From Table 15-6. C = 0.006.
No value of P has been established for forest.
Using Eq. 15-6: A = 185 × 0.33 × 1.5 × 0.006 × 1.0 = 0.66 tons/ac/y.
The total sheet and rill erosion from the 600-ac watershed is (280 × 2.95) + (170 × 1.18) + (150 × 0.66) = 1126 tons/y.
Using ONLINE USLE2,
the answer for the given data is: Watershed soil loss = 1126.41 tons/y.
De la Fig. 13-2: R = 185.
De la Tabla 13-4, K = 0,38.
De la Fig. 13-3, LS = 1,4.
El valor de C de las tierras de cultivo se obtiene de fuentes locales; asuma C = 0,12 para este
ejemplo.
De la Tabla 13-7, R = 185; K = 0.38: LS = 1.4.
De la Tabla 13-5, C = 0,012.
El valor de P no se ha establecido para pastos; por lo tanto, P = 1.
Utilizando la Ec. 13-6: A = 185 × 0.38 × 1.4 × 0.012 × 1.0 = 1.18 toneladas/ac/a.
R = 185.
De la Tabla 13-4, K = 0.33.
De la Fig. 13-3, LS = 1,8.
De la Tabla 13-6, C = 0,006.
El valor de P no se ha establecido para bosques.
Utilizando la Ec. 13-6: A = 185 × 0.33 × 1.5 × 0.006 × 1.0 = 0,66 toneladas/ac/a.
El total de erosión en surcos de la cuenca de 600 acres es: (280 × 2,95) + (170 × 1,18) + (150 × 0.66) = 1126 toneladas/año.
Utilizando ENLINEA USLE2,
el resultado es: Pérdida de suelo = 1126,41 toneladas/año.
|
Erosión de Canal
Channel erosion includes gully erosion, streambank erosion, streambed degradation, floodplain scour, and other sources of sediment, excluding upland erosion. Gullies are incipient channels in process of development. Gully growth is usually accelerated by severe climatic events, improper land use, or changes in stream base levels. Most of the significant gully activity, in terms of the quantities of sediment produced and delivered to downstream locations, is found in regions of moderate to steep topography having thick soil mantles. The total sediment outflow from gullies is usually less than sheet and rill erosion [33].
La erosión de canales incluye erosión de cárcavas, erosión del lecho de los ríos, la degradación del lecho, erosión de las llanuras aluviales y otras fuentes de sedimentos, exluyendo la erosión de las tierras de cabecera. Los barrancos son canales incipientes en proceso de desarrollo. El crecimiento de las cárcavas generalmente se ve acelerado por eventos climáticos severos, el uso inapropiado de la tierra, o por cambios en el nivel de base de la corriente. La mayor parte de la actividad de cárcava significativa, en términos de las cantidades de sedimentos producidos y entregados en lugares aguas abajo, se encuentra en regiones de topografía moderada a empinada, con mantos gruesos de suelo. La salida total de sedimentos de las cárcavas suele ser menor que la erosión de la lámina y surco [33].
Streambank erosion and streambed degradation can be significant in certain cases. Changes in channel alignment and/or removal of natural vegetation from stream banks may cause increased bank erosion. Streambed degradation, typically downstream of reservoirs, can also constitute an additional source of sediment (Fig. 15-4).
La erosión del lecho de un río y la degradación del cauce pueden ser importantes en ciertos casos. Los cambios en la alineación de los canales y/o la eliminación de la vegetación natural de los bancos de arroyos pueden causar una mayor erosión de los bancos. La degradación del lecho de arroyos, típicamente aguas abajo de los embalses, también puede constituir una fuente adicional de sedimentos (Fig. 13-4).
Figure 15-4 Erosión hasta el lecho rocoso aguas abajo de una presa de retención de sedimentos. |
Los métodos para determinar la pérdida de suelo debido a los diferentes tipos de erosión de canal son:
Comparar fotografías aéreas tomadas en diferentes momentos para evaluar la tasa de crecimiento de los canales.
Realizar levantamientos transversales de ríos para determinar cambios en el área de la sección transversal.
Ensamblar datos históricos para determinar la edad promedio y la tasa de crecimiento de los canales, y
Realizar estudios de campo para evaluar la tasa de crecimiento anual de los canales.
Los estudios de campo a menudo pueden proporcionar datos suficientes para estimar la erosión del banco de arena de la siguiente manera [44]:
| S = H L R | (13-7) |
en la cual:
S = volumen anual de erosión del banco;
H = altura media de banco;
L = longitud del banco erosionado, a
cada lado del canal, si ambas partes están erosionando; y
R = tasa anual de recesión del banco (tasa neta si un lado está erosionando mientras que el otro está depositando).
La degradación del lecho se puede estimar de la siguiente manera [44]:
| S = W L D | (13-8) |
en la cual:
S = volumen anual de degradación del cauce;
W = ancho inferior promedio de degradación del canal;
L = longitud de degradación del canal; y
D = tasa anual de degradación del cauce.
Erosión acelerada debido a actividades de minería a tajo abierto y construcción
Las actividades de minería a tajo abierto y construcción aceleran enormemente las tasas de erosión. Por ejemplo, Collier y otros [10] encontraron que una cuenca con un 10.4 por ciento de su superficie extraída de la mina erosionó 76 veces más sedimento que una cuenca similar sin perturbación. Wolman y Shick [48] encontraron que las concentraciones de sedimentos en las corrientes que drenan áreas de construcción oscilaban entre 3 mil y 150 mil ppm, en comparación con las concentraciones de 2 mil ppm en entornos naturales comparables. Estos estudios indican que las perturbaciones del terreno natural inducidas por acción humana tienen un gran impacto en la producción de sedimentos. Con una elección cuidadosa de factores, la EUPS se puede usar para calcular la pérdida de suelo en áreas disturbadas.
Rendimiento de sedimentos
En aplicaciones de ingeniería, la cantidad de sedimento erosionado en las fuentes no es tan importante como la cantidad de sedimento entregado a un punto aguas abajo, es decir; el rendimiento de sedimentos.
El rendimiento de sedimentos se calcula multiplicando la producción bruta de sedimentos, que incluye todos los tipos de erosión (erosión de lámina, arroyo, barranca, y canal) por una relación de entrega de sedimentos que varía en el rango de 0 a 1 (también se puede expresar como porcentaje). Por lo tanto, un cálculo del rendimiento de sedimentos depende de una estimación de la producción bruta de sedimentos (de las diversos fuentes) y una razón apropiada de entrega de sedimentos.
Razón de entrega de sedimentos
La relación de entrega de sedimentos (RES)
es función de los siguientes factores:
(1) fuente de sedimentos, (2) proximidad de la fuente de sedimentos al
sistema de transporte fluvial,
The sediment source has an influence on the delivery ratio. Not all sediments originating in sheet and rill erosion are likely to enter the fluvial transport system; however, sediments produced by channel erosion are generally closer to the transport system and are more likely to be delivered to downstream points. The proximity of the sediment source to the transport system is also an important variable in the estimation of the SDR. The amounts of sediment delivered to downstream points will depend to a large extent on the ability of the fluvial transport system to entrain and hold on to the sediment particles. Silt and clay particles can be transported much more readily than sand particles; therefore, the delivery of silts and clays is more likely to occur than that of sands. Catchment characteristics also affect sediment delivery ratios. High relief often indicates both a high erosion rate and a high SDR. High channel density is usually an indication of an efficient transport system and, consequently, of a high SDR.
La fuente de los sedimentos tiene una influencia sobre la relación de entrega de sedimentos (RES).
Estimación de relaciones de entrega de sedimentos. La RES es la relación entre el rendimiento de sedimentos y la producción bruta. La producción de sedimentos puede ser evaluada por uno de varios métodos. En los sitios de depósito, estimaciones de la producción de sedimentos se pueden obtener por medio de levantamientos de campo. Alternativamente, la producción de sedimentos puede ser evaluada por medición directa de la carga de sedimentos en el punto de interés. Estimaciones de la producción bruta de sedimentos de tierras altas se pueden obtener utilizando la fórmula EUPS o una fórmula derivada regionalmente. Cuando sea justificado, esta estimación puede ser aumentada por estimaciones de erosión de barranco y canal.
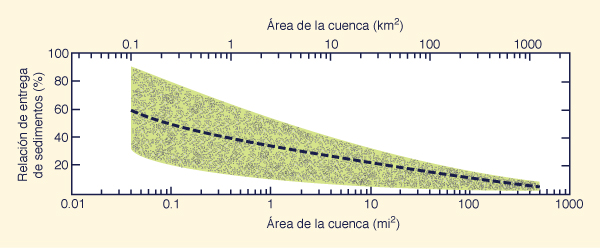
En ausencia de mediciones, se puede utilizar un análisis estadístico para desarrollar ecuaciones de regresión para predecir el valor de RES. La ecuación de predicción RES más simple es la que se basa únicamente en el área de drenaje, como se muestra en la Fig. 13-5. Esta figura muestra que el RES varía aproximadamente en proporción inversa a la potencia 1/5 del área de drenaje. Otras fuentes, sin embargo; indican valores tan bajos como 1/8 [2]. El hecho es que cuanto mayor sea el área de drenaje, menor será la pendiente del terreno y mayores las posibilidades para la deposición de sedimentos en algún lugar dentro de la cuenca; en consecuencia, menor el valor de RES. La Figura 13-5 proporciona aproximaciones al valor de RES, pero para estudios más refinados se recomienda su uso con cuidado.
Figura 13-5 Relación de entrega de sedimentos vs área de la cuenca [44]. |
Un ejemplo del uso del análisis estadístico para la estimación del valor de la relación de entrega de sedimentos está dada por Roehl [37]. Utilizando datos de la región de Piamonte al sureste de los Estados Unidos, Roehl desarrolló la siguiente ecuación:
|
L
SDR = 31,623 (10A )-0.23 (_____) -0.51 B -2.79 R | (13-9) |
en la cual:
RES = relación de entrega de sedimentos;
A = área de la cuenca, en millas cuadradas;
L / R = relación entre la longitud y diferencia de elevación (longitud L medida paralelamente al drenaje principal; la diferencia de elevación R se mide entre la cabecera y la salida de la cuenca); y
B = relación de bifurcación media, definida como la relación entre el número de corrientes en un orden dado y el número de corrientes en el orden superior inmediato.
Los valores de RES tomados por Roehl en el área de Piedmont estaban en el rango de 3,7 a 59,4 por ciento.
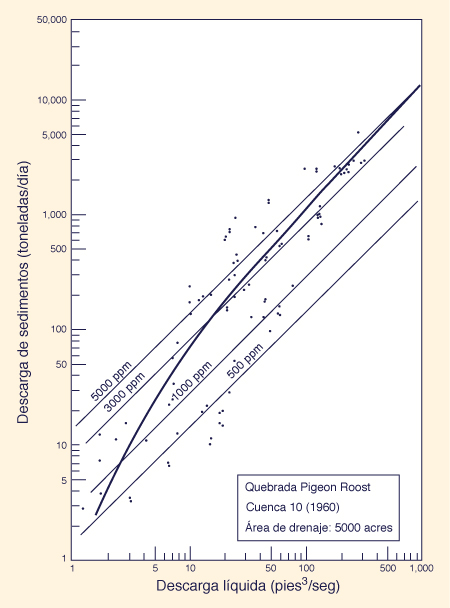
Fórmulas empíricas para el rendimiento de sedimentos
Así como el RES, el análisis estadístico se puede utilizar para desarrollar ecuaciones regionales para la predicción del rendimiento de sedimentos. Un estudio realizado por Dendy y Bolton [13] mostró que la producción de sedimentos puede estar relacionado con el área de influencia y la escorrentía anual media.
Rendimiento de sedimentos vs área de la cuenca. Dendy y Bolton estudiaron los datos de sedimentación de aproximadamente 1500 embalses, estanques, y presas de retención de sedimentos. En el desarrollo de sus fórmulas, utilizaron datos de alrededor de 800 de estos embalses con áreas de drenaje mayor o igual a 1 milla cuadrada. Las cuencas más pequeñas (áreas de drenaje menores a 1 milla cuadrada) fueron excluidas debido a su gran variabilidad en el rendimiento de sedimentos, reflejando los efectos de los suelos, tipo de terreno, vegetación, uso de la tierra y prácticas agrícolas.
Para áreas de drenaje entre 1 y 30.000 millas2, Dendy y Bolton encontraron que el rendimiento anual de sedimentos, por unidad de superficie, era inversamente proporcional a la potencia 0,16 del área de drenaje:
|
S A
____ = (_____) -0,16 SR AR | (13-10) |
en la cual:
S = rendimiento de sedimentos, en toneladas por milla cuadrada por año;
SR = rendimiento de sedimentos de referencia, correspondiente a una milla cuadrada de área de drenaje, igual a 1645 toneladas por año;
A = área de drenaje, en millas cuadradas; y
AR = área de drenaje de referencia (1 milla cuadrada).
Rendimiento de sedimentos vs escurrimiento anual medio. Dendy y Bolton estudiaron datos de sedimentación
de quinientos cinco (505) reservorios con datos de escurrimiento anual medio.
Para Q < 2 pulgadas:
|
S
_____ = 1.07 (Q/QR) 0.46 SR | (13-11a) |
Para Q ≥ 2 pulgadas:
|
S
_____ = 1.19 e -0.11(Q/QR) SR | (13-11b) |
en las cuales QR = escurrimiento anual medio de referencia, QR = 2 pulgadas.
Dendy y Bolton combinaron las Ecs. 13-10 y 13-11 en un conjunto de ecuaciones para expresar el rendimiento del sedimento en términos del área de drenaje y el escurrimiento anual medio.
Para Q < 2 pulgadas:
|
S Q A
_____ = 1.07 ( ______ ) 0.46 [ 1.43 - 0.26 log ( ______ ) ] SR QR AR | (13-12a) |
Para Q ≥ 2 pulgadas:
|
S A
_____ = 1.19e -0.11(Q/QR) [ 1.43 - 0.26 log ( ______ ) ] SR AR | (13-12b) |
Dados SR = 1645 ton/mi2/a, QR = 2 pulgadas, y AR = 1 mi2, la Ec. 15-12 se reduce a:
Para Q < 2 pulgadas:
| S = 1280 Q 0.46 (1.43 - 0.26 log A) | (13-13a) |
Para Q ≥ 2 pulgadas:
| S = 1965 e -0.055Q (1.43 - 0.26 log A) | (13-13b) |
Las Ecuaciones 13-12 y 13-13 se basan en valores promedio de datos agrupados; por lo tanto, deben ser utilizados con precaución. En ciertos casos, factores locales como suelos, geología, topografía, uso del suelo y vegetación pueden tener una mayor influencia en el rendimiento de los sedimentos que el escurrimiento anual medio o el área de drenaje. Sin embargo, estas ecuaciones proporcionan una primera aproximación a la evaluación regional del rendimiento de sedimentos para propósitos de planificación de cuencas hidrográficas.
Ejemplo 13-5.
Calcular la producción de sedimentos por la fórmula Dendy y Bolton para una cuenca de 150-mi2 con
La aplicacióm de la Ec. 13-13b lleva a:
Por lo tanto, la producción de sedimentos es 210,123 ton/año.
Utilizando ENLINEA DENDY-BOLTON,
la respuesta para los datos dados es: Producción de sedimentos = 210123,47 toneladas/año.
|
Otras fórmulas ampliamente usadas para la producción de sedimentos son la Ecuación Universal Modificada de Pérdida de Suelo (EUMPS) desarrollada por Williams [45] y, la fórmula de Flaxman [17]. A diferencia de la EUPS, que se basa en valores anuales, la EUMPS está diseñada para usarse con eventos, es decir, tormentas individuales. La fórmula de Flaxman fue desarrollada usando datos del Oeste de los Estados Unidos y por lo tanto es particularmente aplicable a esa región. `
13.3 TRANSPORTE DE SEDIMENTOS
|
|
El transporte de sedimentos se refiere al arrastre y movimiento de sedimentos por el agua que fluye. El conocimiento de los principios del transporte de sedimentos es esencial para la interpretación y solución de diversos sistemas hidráulicos, problemas hidrológicos y de la ingeniería de recursos hídricos.
El estudio del transporte de sedimentos puede dividirse en:
Mecánica del transporte de sedimentos,
Predicción del transporte de sedimentos, y
Enrutamiento de sedimentos.
La mecánica de transporte de sedimentos se refiere a los procesos fundamentales por los cuales el sedimento es arrastrado y transportado por el flujo del agua.
La predicción del transporte de sedimentos se refiere a los métodos y técnicas para predecir la tasa de transporte de sedimentos en equilibrio en arroyos y ríos. La predicción del transporte de sedimentos se realiza mediante una fórmula de transporte de sedimentos.
El enrutamiento de sedimentos se refiere a los procesos de transporte de sedimentos en no equilibrio, es decir, bajo flujo inestable, cuyo resultado es la agradación o degradación de lechos aluviales.
La descripción del transporte de sedimentos se basa en principios de mecánica de fluidos, mecánica de ríos y geomorfología fluvial. La energía y la turbulencia del flujo dan a los arroyos y ríos la capacidad de arrastrar y transportar sedimentos. El sedimento que se transporta puede originarse en: (a) cuencas de cabecera, ó (b) canales propriamente dichos.
Una característica importante del transporte de sedimentos es el arrastre y transporte por el flujo del material que constituye el lecho de la corriente. Por lo tanto, el transporte de sedimentos sirve no sólo como medio para el movimiento de los sedimentos de aguas arriba a aguas abajo, sino también como mecanismo por medio del cual los arroyos y ríos determinan la forma de su sección transversal y, consecuentemente, su rugosidad. Mientras que el transporte de sedimentos es un tema de mecánica de fluidos, la interacción entre la corriente que fluye y su frontera (o límite) es un tema de hidráulica fluvial, o mecánica de ríos.
Mecánica del transporte de sedimentos
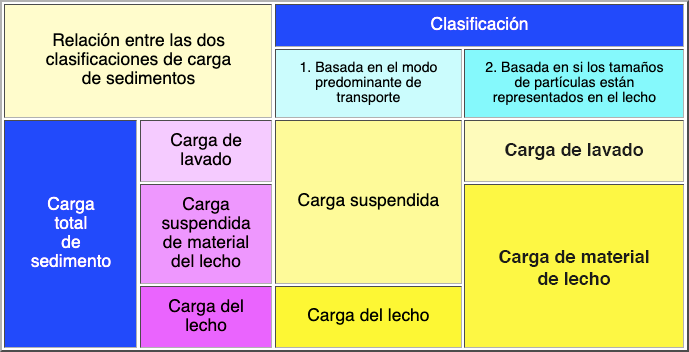
La carga de sedimentos, también denominado caudal sólido,
es la cantidad total de sedimento
transportado por un arroyo o río en un punto determinado, expresado en términos de peso por unidad de tiempo.
En función del modo de transporte predominante,
la carga de sedimentos se puede clasificar en: (a) carga del lecho, y (b) carga suspendida.
La carga del lecho es la fracción de la carga de sedimento
que se mueve por saltado y rodadura a lo largo
del lecho del canal, principalmente
por la acción de los esfuerzos de corte del fondo causados por el gradiente
vertical de velocidad prevaleciente.
En función de si los tamaños de partículas están representados en el lecho del río,
la carga de sedimentos se puede
clasificar en: (a) carga de material del lecho, y (b) carga de material fino.
La Figura 13-6 muestra la relación entre las dos clasificaciones de carga de sedimentos [11].
Figura 13-6 Relación entre las dos clasificaciones de carga de sedimentos [11]. |
Inicio del Movimiento. El agua que fluye sobre el lecho de una corriente tiene un marcado gradiente vertical de velocidad en las proximidades del lecho. Este gradiente de velocidad ejerce un esfuerzo cortante sobre las partículas que se encuentran en el lecho, es decir; un esfuerzo cortante en el fondo. Para canales hidráulicamente anchos, el esfuerzo cortante en el fondo se puede aproximar mediante la siguiente fórmula [5]:
| τo = γ d So | (13-14) |
en la cual
τo = esfuerzo cortante de fondo;
γ = peso específico del agua;
d = profundidad de flujo; y
Hay un valor límite del esfuerzo cortante de fondo
por encima del cual las partículas comienzan a moverse.
Este valor se conoce como esfuerzo cortante de fondo crítico, o esfuerzo de tracción crítico.
Las determinaciones del esfuerzo de tracción crítico,
para condiciones dadas de flujo y sedimento, son en gran medida de naturaleza
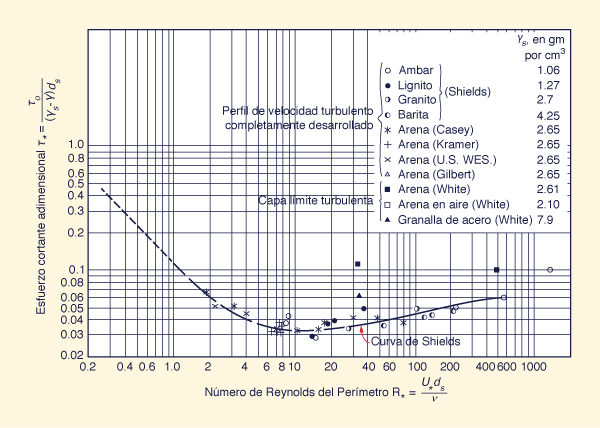
empírica. La curva de Shields, mostrada en
Figura 13-7 Diagrama de Shields para la iniciación del movimiento [2]. |
La abscisa en el diagrama de Shields es el número de Reynolds del perímetro:
|
U* ds
R* = _______ ν | (13-15) |
en la cual R* = número de Reynolds del perímetro; U* = velocidad de corte; ds = diámetro medio de las partículas; y v = viscosidad cinemática del agua. La velocidad de corte se define como sigue:
|
τo
U* = (____)1/2 ρ | (13-16) |
en la cual ρ = densidad del agua. La ordenada en el diagrama de Shields es el esfuerzo cortante adimensional:
|
τo
τ* = ____________ (γs - γ) ds | (13-17) |
en la cual τ* = esfuerzo cortante adimensional.
El diagrama de Shields indica que, dentro de un rango medio de números de Reynolds del perímetro (aproximadamente 2-200), el esfuerzo cortante crítico adimensional puede tomarse como una constante para propósitos prácticos. Por lo tanto, dentro de este rango, el esfuerzo cortante crítico es proporcional al tamaño de la partícula. Por ejemplo, asumiendo un valor de esfuerzo cortante crítico adimensional τ* = 0.04 (del diagrama de Shields, Fig. 13-7), la Ecuación 13-17 conduce a lo siguiente:
| τc = 0.04 (γs - γ) ds | (13-18) |
en la cual τc = esfuerzo cortante crítico.
Para partículas de cuarzo (γs
= 2.65 × 62.4 lb/pie3),
la
| τc = 0.34 ds | (13-19) |
en la cual el esfuerzo cortante crítico está dado en libras por pie cuadrado y el diámetro de las partículas en pulgadas. Los extensos estudios experimentales realizados por Lane [30] han demostrado que el coeficiente de la Ec. 13-19 es alrededor de 0.5. Lane, sin embargo, usó el tamaño de partícula d75 (es decir, el diámetro para el cual el 75% en peso es más fino) en lugar del diámetro medio (d50) utilizado por Shields.
Ejemplo 13-6.
Utilizando el criterio de Shields para la iniciación del movimiento, determinar si
una partícula de cuarzo de diámetro 3 mm
está en reposo o en movimiento bajo la acción de un canal con flujo de 7 pies de profundidad
y pendiente S0 = 0.0001.
Asumir la temperatura del agua 70°F.
De la Ec. 13-14, el esfuerzo cortante de fondo es:
τo = 62.4 × 7 × 0.0001 = 0.0437 lb/pie2.
De la Ec. 13-17, el esfuerzo cortante adimensional es: τ*
= 0.0437/ [(2.65 - 1.0) ×
62.4 × 3 / (25.4 × 12)] = 0.0431.
De la Ec. 13-16, la velocidad de corte es: U* = (0.0437/1.94)1/2 = 0.15 pies/s.
De la Tabla A-2, la viscosidad cinemática es: 1.058 x 10-5 pies2/s.
De la Ec. 13-15, el número de Reynolds del perímetro es: R* = 0.15 × [3 / (25.4 × 12)] / (1.058 × 10-5) = 140.
Para R* = 140,
el esfuerzo cortante crítico
adimensional se obtiene de la curva de Shields (Fig. 13-7): τ*c = 0.048.
Dado que τ* = 0.0431 es menor que τ*c = 0.048,
se concluye que la particula está en reposo.
Empleando ENLINEA SHIELDS,
la respuesta es: No hay movimiento. Por lo tanto, la partícula se encuentra en reposo.
|
Formas de rugosidad del lecho. Los arroyos y ríos son los arquitectos de su propia geometría.
Las formas de rugosidad del lecho son configuraciones tridimensionales de material del lecho, las cuales
se forman en los cauces aluviales por acción del flujo.
Estas formas modifican la cantidad de fricción; se desarrollan
durante flujos bajos (régimen de flujo bajo), sólo para ser obliteradas durante flujos altos (régimen de flujo alto) [40].
Entonces, la fricción se compone de dos partes: (1) fricción, o rugosidad de grano y (2) fricción, o rugosidad
de forma.
La rugosidad de grano es una función del tamaño de las partículas; la rugosidad de
forma es una función del tamaño y
extensión de la forma del lecho.
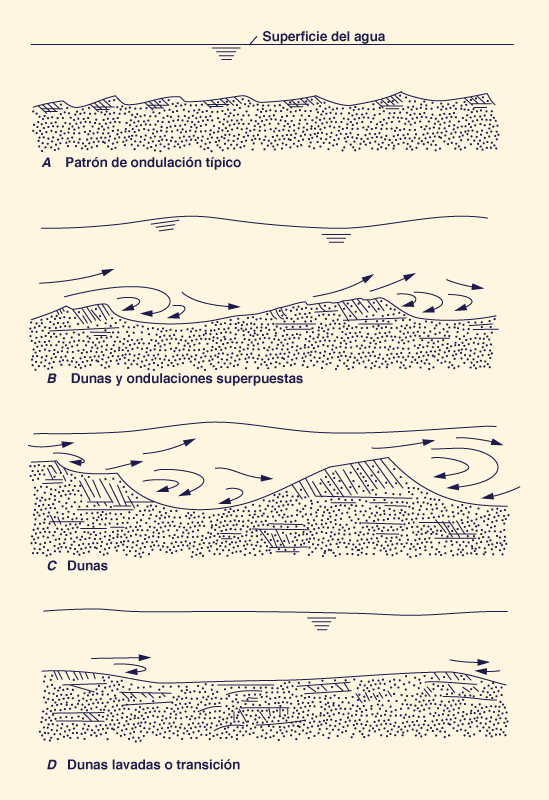
Estudios detallados han demostrado que pueden existir varias formas de rugosidad del lecho
en los fondos de los ríos, dependiendo
de la energía y la capacidad de transporte del material del lecho.
|
|
|
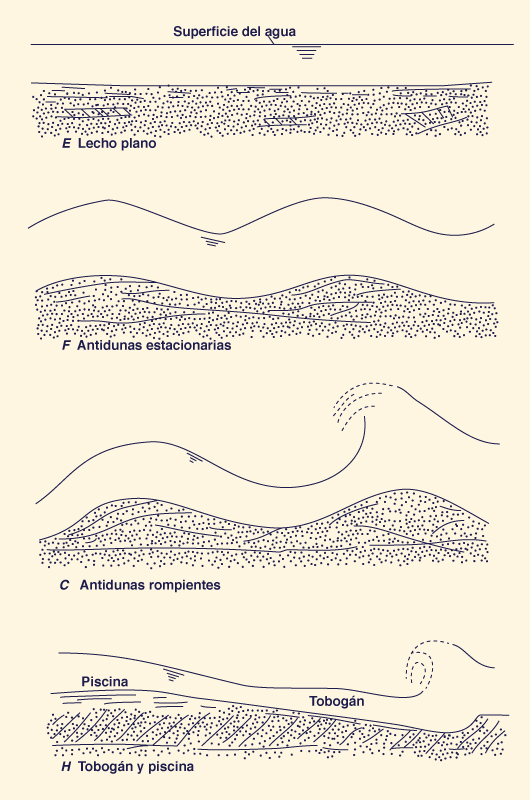
Figura 13-8 Formas de rugosidad del lecho en canales aluviales [40].
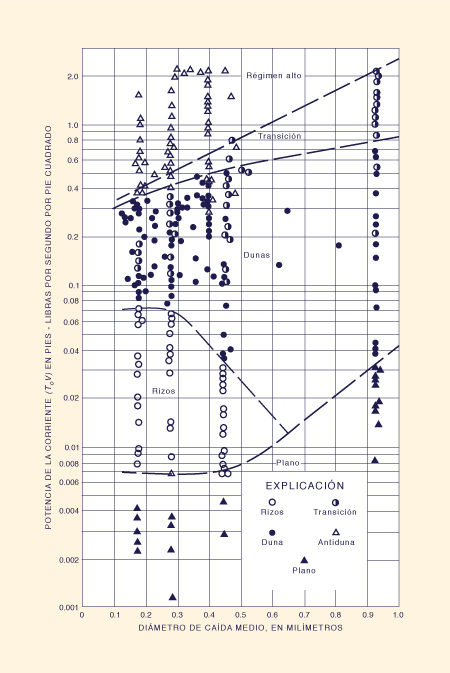
Puede demostrarse que la ocurrencia de diferentes formas de rugosidad del lecho está relacionada con el diámetro medio
de las partículas que forman el lecho y con la potencia de la corriente
El lecho plano con movimiento (de sedimento) representa la condición en la cual la potencia de la corriente es lo suficientemente grande como para obliterar las dunas, eliminando esencialmente la rugosidad de forma. El lecho plano representa la condición de fricción de fondo mínima. Para valores más altos de potencia de la corriente, las antidunas (régimen superior) se forman junto con las ondas superficiales, con la tendencia al movimiento hacia aguas arriba, generalmente bajo flujo supercrítico. Para valores aún mayores de potencia de la corriente, por ejemplo; en flujos en corrientes muy empinadas, la configuración del lecho se asemeja a una secuencia de toboganes y piscinas [40].
Figura 13-9 Forma de la rugosidad del lecho vs
potencia de la corriente |
La evaluación de la forma de rugosidad del lecho tiene implicaciones prácticas para la ingeniería hidrológica. La forma de rugosidad del lecho determina los valores de rugosidad; a su vez, éstos determinan las profundidades del río. Por ejemplo, las ondulaciones, o rizos, se asocian con valores de Manning n en el rango de 0.018 a 0.030, constituyendo, en general la forma de rugosidad una fracción de la rugosidad de grano.
Sin embargo; las dunas están asociadas con valores de n en el rango de 0.020 a 0.040, con la rugosidad de forma del mismo orden de magnitud que la rugosidad de grano. Además, el lecho plano con movimiento de sedimento está asociado con valores relativamente bajos de n, en el rango de 0.012 a 0.015; y en este caso, la rugosidad de forma es mínima.
La evaluación apropiada de la fricción de fondo, incluida su variación a medida que el flujo cambia del régimen inferior (rizos, rizos en dunas, y dunas) al régimen superior (lecho plano con movimiento de sedimentos, antidunas, y toboganes y pozas) es un tema importante en la ingeniería hidrológica y en la hidráulica fluvial.
Concentration of Suspended Sediment. For a given volume of water-sediment mixture, the suspended-sediment concentration is the ratio of the weight of dry sediment to the weight of the water-sediment mixture, expressed in parts per million. To convert the concentration in ppm to milligrams per liter (mg/ L), the applicable factor ranges from 1.0 for concentrations between 0 and 15,900 ppm, to 1.5 for concentrations between 529,000 and 542,000 ppm, as shown in Table 15-8.
Concentración de sedimentos en suspensión.
Para un volumen dado de mezcla de sedimentos y agua,
la concentración del sedimento en suspensión es la relación
entre el peso del sedimento seco y el peso de la mezcla (de
agua y sedimento), expresada en partes por millón (ppm).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The suspended-sediment concentration varies with the flow depth, usually being higher near the stream bed and lower near the water surface. The coarsest sediment fractions, typically those in the sand size, exhibit the greatest variation in concentration with flow depth. The finer fractions, i.e., silt and clay particles, show a tendency for a nearly uniform distribution of suspended-sediment concentration with flow depth.
La concentración del sedimento en suspensión varía con la profundidad de flujo,
siendo generalmente más alta cerca del fondo (o lecho), y más baja cerca de la superficie del agua.
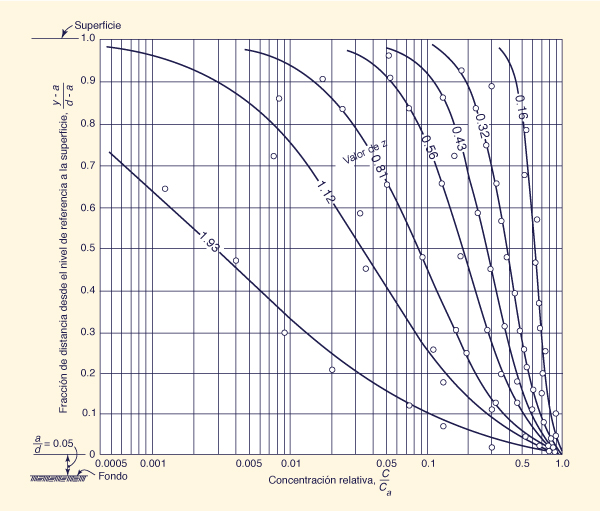
La Figura 13-10 muestra la variación de la concentración de sedimentos en suspensión con la profundidad de flujo. En esta figura, y es la fracción de la profundidad de flujo medida desde el fondo del canal o corriente, a es la distancia de referencia, medida desde el fondo del canal, y d es la profundidad de flujo. El eje de las abscisas muestra la relación adimensional C/Ca, en la cual Ca es la concentración de sedimentos en la distancia de referencia, y C es la concentración de sedimentos a una distancia (y - a). El valor de a es pequeño en comparación con el valor de d. La Fig. 13-10 es específicamente para el caso de a/d = 0,05. El eje de las ordenadas muestra la relación adimensional (y - a)/(d - a). El parámetro de la curva z es el número de Rouse, el cual se define de la siguiente manera:
|
w
z = _________ β κ U* | (13-20) |
en la cual z = número de Rouse (adimensional); w = velocidad de caída de las partículas de sedimento; β = coeficiente que relaciona la transferencia de masa y cantidad de movimiento (β ≅ 1 para sedimentos finos); κ = constante de von Karman (κ = 0.4 para líquidos claros); y U* = velocidad de corte (Ec. 13-16). De la Fig. 13-10, puede observarse que para números de Rouse altos, la variación de la concentración de sedimentos en suspensión a lo largo de la profundidad de flujo es bastante marcada. Por el contrario, para números de Rouse bajos, existe la tendencia para una mayor uniformidad de la concentración de sedimentos en suspensión a través de la profundidad de flujo.
Figura 13-10 Variación de la concentración de sedimentos en suspensión a través de la profundidad de flujo [2]. |
Predicción del Transporte de Sedimentos
En la práctica, la carga de sedimentos, descarga de sedimentos, y la tasa de transporte de sedimentos son sinónimos. Sin embargo, carga de fondo, carga suspendida de material de lecho, y carga de lavado son mutuamente excluyentes. La predicción del transporte de sedimentos se refiere a la estimación de las tasas de transporte de sedimentos bajo condiciones de flujo de equilibrio, es decir, flujo permanente.
Hay numerosas fórmulas para la predicción del transporte de sedimentos [2]. La mayoría de las fórmulas calculan solamente la carga de material de lecho, que consiste en: (1) carga de fondo, y (2) carga suspendida de material de lecho. Algunas calculan la carga total de sedimentos, la cual consta de: (1) carga de fondo, (2) carga suspendida de material de lecho, y (3) carga de lavado. Sin embargo, algunas fórmulas pueden calcular la carga de fondo y la carga suspendida de material de lecho, por separado. Invariablemente, las fórmulas de transporte de sedimentos tienen algunos componentes empíricos y, por lo tanto, son más aplicables dentro del rango de datos de laboratorio y/o de campo que fueron utilizados para su desarrollo.
Fórmula de Duboys. La fórmula de Duboys es ampliamente reconocida como uno de los primeros intentos de desarrollar una fórmula para el transporte de sedimentos. La fórmula es la siguiente [14]:
| qs = ψD τo ( τo - τc ) | (13-21) |
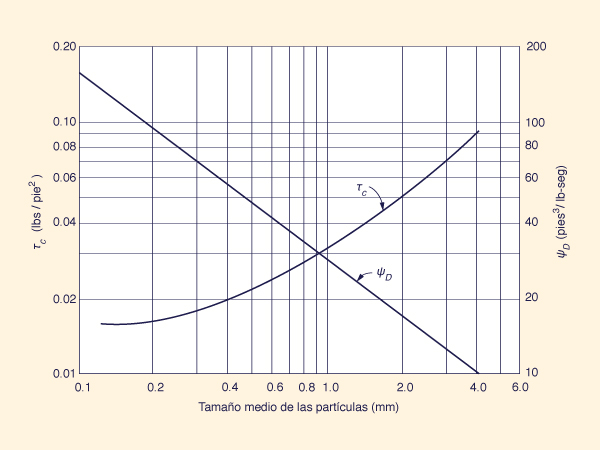
en la cual qs = tasa de transporte de material de lecho, por unidad de ancho, en libras por segundo, por pie; ψD = parámetro, el cual es función del tamaño de las partículas, en pies cúbicos por libra, por segundo; τo = esfuerzo cortante de fondo, en libras por pie cuadrado; y τc = esfuerzo cortante crítico, en libras por pie cuadrado. La Figura 13-11 muestra los valores de ψD y τc a ser usados en la ecuación de Duboys (Ec. 13-21) [3].
Figure 13-11 Valores de ψD y τc para uso en la fórmula de Dubois [2]. |
Ejemplo 13-7.
Dado un canal de profundidad media d = 12 pies,
ancho medio b = 320 pies;
pendiente de equilibrio So = 0.0001,
y tamaño medio de las partículas d50 = 0.6 mm,
calcular la tasa de transporte de material del lecho usando la fórmula de Duboys.
Usando la Ec. 13-14: τo = 62.4 × 12.0 × 0.0001 = 0.07488 lb/pie2.
De la Fig. 13-11: ψD = 42 pies3/lb/s.
De la Fig. 15-11:
τc = 0.025 lb/pies2.
De la Ec. 13-21: qs = 42 × 0.07488 × (0.07488 - 0.025) = 0.157 lb/s/ft.
Por lo tanto: Qs = qs b = 0.157 × 320 = 50.2 lb/s.
Utilizando ENLINEA DUBOYS,
la respuesta es: Qs = 50.551 lb/s, lo cual es equivalente a 2,183.821 tons/día.
|
Fórmula de Meyer-Peter. El desarrollo de la fórmula de Meyer-Peter se basó en datos de canales artificiales, con material del lecho de tamaño uniforme, en el rango de 3 a 28 mm. Estos sedimentos gruesos no producen formas de fondo apreciables; por consiguiente, la fórmula es aplicable al transporte de sedimentos gruesos, para los cuales la forma de rugosidad es despreciable. La fórmula de Meyer-Peter es la siguiente [2, 35]:
| qs = ( 39.25 q 2/3 So - 9.95 d50 ) 3/2 | (13-22) |
en la cual qs = tasa de transporte de material de lecho, por unidad de ancho, en libras por segundo por pie; q = descarga líquida por unidad de ancho, en pies cúbicos por segundo por pie; So = pendiente de equilibrio; y d50 = tamaño medio de las partículas, en pies.
Ejemplo 13-8.
Dado un canal de profundidad media d = 2 pies;
ancho medio b = 25 pies;
velocidad media v = 6 pies por segundo;
pendiente
La descarga por unidad
de ancho es: q = vd = 6 x 2 = 12 pies3/s/pie.
De la Ec. 13-22: qs = { ( 39.25 x 12 2/3 x 0.008 ) - [ 9.95 x 22 / (25.4 x 12) ] } 3/2 = 0.894 lb/pie.
Por lo tanto: Qs = qs b = 22.35 lb/s.
Usando
ENLINEA MEYER-PETER,
La respuesta es: Qs = 22.337 lb/s, lo cual es equivalente a 964.941 toneladas/día.
|
Función de carga de lecho de Einstein. En 1950, Hans Einstein publicó un procedimiento para el cálculo de la tasa de transporte de material de lecho por fracciones de tamaño [15]. El método fue desarrollado en base a consideraciones teóricas de flujo turbulento, apoyados por datos de laboratorio y de campo. A Einstein se le atribuye varios conceptos novedosos en la teoría del transporte de sedimentos, incluyendo la separación de la fricción de fondo en rugosidad de forma y de grano, y el uso de las propiedades estadísticas de turbulencia para explicar la mecánica del transporte de sedimentos.
La función de carga de lecho de Einstein calcula primero
la tasa de transporte de carga de lecho.
Método de Einstein Modificado. El Método de Einstein Modificado fue desarrollada por Colby y Hembree [6] para incluir mediciones actuales de carga suspendida en el marco del método original de Einstein. Por lo general, las mediciones de carga suspendida no incluyen: (a) la carga del lecho, y (b) la fracción de carga suspendida que se mueve muy próximo al lecho para ser muestreado con precisión. El Método de Einstein Modificado calcula la carga total de sedimentos, por fracciones de tamaño, en base a mediciones de carga suspendida y a las características geométricas e hidráulicas del arroyo o río. Los detalles del método han sido reportados en la literatura [2, 6].
Método de Colby 1957 . El método de Colby 1957 se basa en algunas de las mismas mediciones que llevaron al desarrollo del Método de Einstein Modificado. Sin embargo, a diferencia de este último, el metodo Colby 1957 no tiene en cuenta la tasa de transporte de sedimentos por fracciones de tamaño. En vez de esto, proporciona la carga total de material de lecho, es decir, la suma de las cargas de material de lecho, medidas y no medidas.
La aplicación del método de Colby 1957 requiere de los siguientes datos:
(1) Profundidad media d,
Utilice la Fig. 13-12 para obtener la descarga de sedimentos no corregida no medida qu' (en toneladas por día, por pie de ancho) en función de la velocidad media.
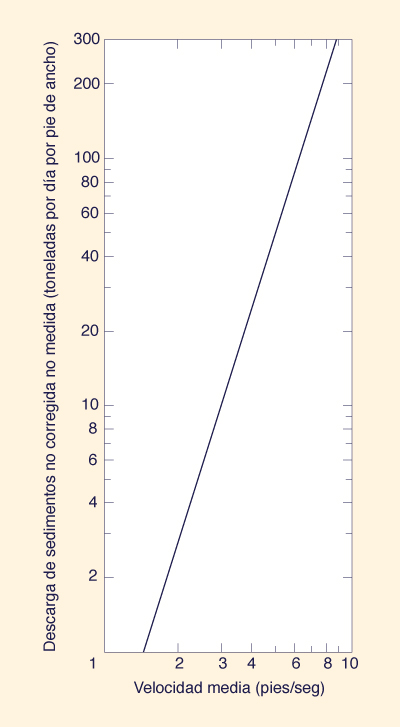
Figure 15-12 Descarga de sedimentos no corregida no medida
vs velocidad media en el método de Colby 1957 [7].Utilice la Fig. 13-13 para obtener la concentración relativa de arenas en suspensión Cr (en partes por millón) en función de la velocidad media y profundidad (de flujo).
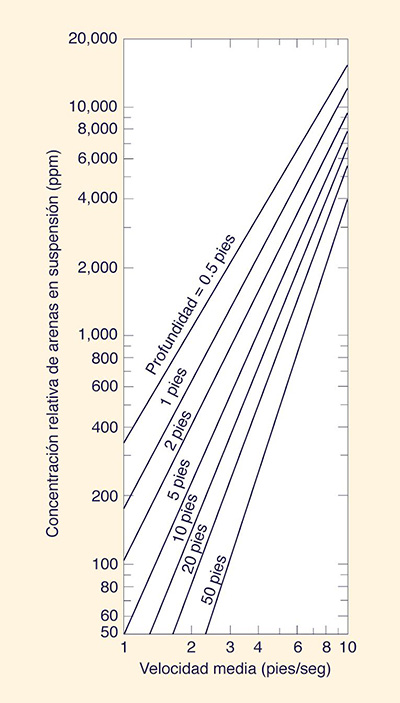
Figura 13-13 Concentración relativa de arenas en suspensión vs
velocidad media y profundidad de flujo en el método de Colby 1957 [7].Calcular la razón de disponibilidad (availability ratio) dividiendo la concentración medida de carga suspendida de material de lecho Cm (ppm) entre la concentración relativa de arenas en suspensión Cr (ppm).
Utilice la línea media de la Figura 13-14 y la razón de disponibilidad para obtener el factor de corrección C, el cual debe ser multiplicado por la carga de sedimentos no medida no corregida qu' para obtener la carga de sedimentos no medida qu (en toneladas por día, por pie).
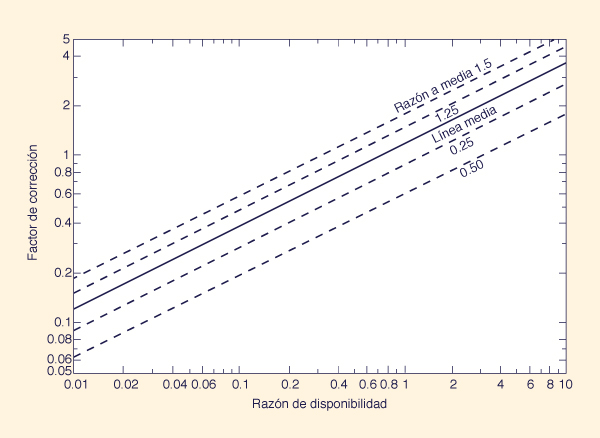
Figure 13-14 Factor de corrección vs razón de disponibilidad en el método de Colby 1957 [7].
-
La descarga total de material de lecho qs es la suma de las descargas de sedimentos medidos y no medidos:
qs = 0.0027 Cm q + qu (13-23)
en la cual qs = descarga de material de lecho,
en toneladas por día, por pie; q = descarga líquida en
pies cúbicos por segundo, por pie; Cm =
concentración medida de la carga suspendida de material
de lecho, en miligramos por litro; y 0.0027 es el
factor de conversión para las unidades indicadas.
Ejemplo 13-9.
Dados
profundidad media d = 10 pies,
ancho medio
b = 300 pies, velocidad media v = 3 pies por segundo,
concentración medida de carga suspendida de material de
lecho Cm = 100 ppm. Calcular la
descarga de material de lecho por el método de Colby 1957.
De la Fig. 13-12, la descarga de sedimentos no
corregida no medida es: qu' = 10 ton/día/pie.
De la Fig. 13-13, la concentración relativa de
arenas en suspensión es Cr = 380 ppm.
Entonces, la razón de disponibilidad es: 100/380 = 0,27.
De la Fig. 13-14, el factor de corrección es C = 0.6.
Por lo tanto: qu = 0.6 × 10 =
6 ton/día/pie.
La descarga líquida,
por unidad de ancho es: q = v d = 3 × 10 =
30 pies3/s/pie.
De la Ec. 13-23, la descarga de sedimentos, por unidad de ancho, es: qs =
(0,0027 × 100 × 30) + 6 = Por lo tanto, la descarga de material de
lecho por el método de Colby 1957 es: Qs = qs b = 14,1 × 300 = 4230 ton/día.
Usando ENLINEA COLBY 1957,
la respuesta es: Qs = 4,231.15 tons/día.
|
Método de Colby 1964. En 1964, Colby publicó un método para calcular la descarga de arena (es decir, la descarga de material de lecho) en los lechos arenosos de corrientes y ríos. El desarrollo del método se guió por la función de carga de lecho de Einstein, contando con el apoyo de grandes cantidades de datos de laboratorio y de campo. El método ha demostrado proporcionar una buena predicción de la tasa de transporte de sedimentos, en particular para las partículas de tamaño arena.
El metodo de Colby 1964 requiere de los siguientes datos: (1) profundidad media d, (2) ancho medio del canal b, (3) velocidad media v, (4) temperatura del agua T, (5) concentración de material fino (es decir, de carga de lavado) Cw , y (6) tamaño medio del material de lecho d50. El procedimiento es el siguiente [8]:
-
Utilice la Figura 13-15 para determinar la descarga de arenas no corregida qu (en toneladas por día por pie) en función de la velocidad media, profundidad de flujo, y tamaño de los sedimentos.
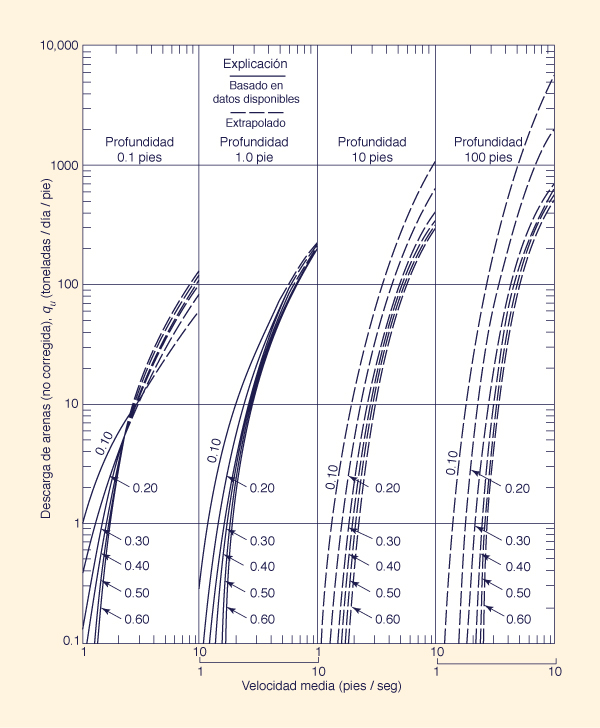
Figura 15-15 Descarga de arenas (no corregida), en función de velocidad media,
profundidad de flujo y tamaño de los sedimentos [9]. -
Para temperatura del agua 60°F, concentración de carga de lavado menos de 1000 ppm (muy pequeña), y tamaño de sedimento en el intervalo de 0,2 a 0,3 mm, no se requieren cálculos adicionales, y qu es la descarga de arenas qs.
-
Para condiciones distintas a la anterior, utilice la Fig. 13-16 para obtener el factor de corrección k1 en función de la profundidad de flujo y temperatura del agua, k2 en función de la profundidad de flujo y la concentración de la carga de lavado, y k3 en función del tamaño medio del material de lecho.
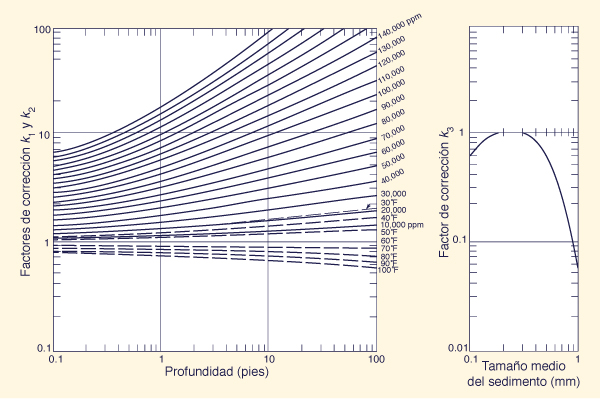
Figura 13-16 Factores de corrección para temperatura del agua (k1), concentración
de carga de lavado (k2), y tamaño medio del material de lecho (k3) [9]. -
La descarga de arenas está dada por la siguiente fórmula:
qs = [ 1 + (k1k2 - 1) k3 ] qu (13-24) en la cual qs = descarga de arenas, en toneladas por día, por pie.
Ejemplo 13-10.
Dados
profundidad de flujo d = 1 pie,
ancho medio del canal b = 30 pies,
velocidad media v = 2 pies/seg,
temperatura del agua 50°F,
concentración de carga de lavado Cw = 10 000 ppm,
y tamaño medio de material de lecho d50 = 0.1 mm.
Calcular la descarga de arenas por el método de Colby 1964.
De la Fig. 13-14: qu = 9 tons/día/pie.
De la Fig. 13-15: k1 = 1.14, k2 = 1.22, y
k3 = 0.6.
De la Ec. 13-24: qs = [ 1 +
(1.14 × 1.22 - 1) × 0.6 ] × 9 = 11.11 tons/día/pie.
Por lo tanto, la descarga de arenas es: Qs = 11.11 × 30 = 333.3 tons/día.
Utilizando ENLINEA COLBY,
la respuesta es: Qs = 333.31 tons/día.
|
Otros métodos para el cálculo de transporte de sedimentos. Se han propuesto varios
otros métodos para el cálculo del transporte de sedimentos.
Entre ellos se destacan los métodos de Ackers y White [1], Engelund-Hansen [16],
Toffaleti [42], y Yang [49].
Los diversos procedimientos varían en complejidad y el rango de aplicabilidad.
Para más detalles sobre éstas y otras fórmulas de transporte de sedimentos, véase [2, 4, 25, 41].
Figura 13-17
Gráfica comparativa de diversas fórmulas |
Curva de gasto de sedimentos
Una curva útil en el análisis del transporte de sedimentos es la curva de gasto de sedimentos, definida como la relación entre descarga sólida y descarga líquida un un lugar de aforo determinado (Fig. 13-17). Para una descarga líquida dada, la curva de gasto de sedimentos permite la estimación de la descarga sólida, o descarga de sedimentos, asumiendo condiciones de flujo estable, o de equilibrio.
The sediment rating curve is an x-y plot showing water discharge in the abscissas and sediment discharge in the ordinates. This plot is obtained either by the simultaneous measurement of water and sediment discharge or, alternatively, by the use of sediment transport formulas. For low-water discharges, the sediment rating curve usually plots as a straight line on logarithmic paper, showing an increase of sediment concentration with water discharge. However, for high water discharges, the sediment rating curve has a tendency to curve slightly downward, approaching a line of equal sediment concentration (i.e., a line having a 45° slope in the x-y plane) (Fig. 5-18).
La curva de sedimentos es un gráfico xy, el cual muestra la descarga líquida en las abscisas y la descarga de sedimentos (descarga sólida) en las ordenadas. Este grafico es obtenido ya sea mediante la medición simultánea de descargas de agua y sedimentos o, alternativamente, con el uso de fórmulas de transporte de sedimentos. Para las descargas liquidas bajas, la curva de sedimentos generalmente es una línea curva en papel logarítmico, mostrando un aumento de la concentración de sedimentos con la descarga l&iacuta;quida. Sin embargo, para las descargas altas, la curva tiene una tendencia a curvarse ligeramente hacia abajo, acercándose a una línea de concentración de sedimentos constante (es decir, una línea que tiene una pendiente de 45°; ver la Fig. 13-18.
Figura 13-18 Curva de gasto de sedimentos típica [2]. |
Like the single-valued stage-discharge rating, the single-valued sediment rating curve is strictly valid only for steady equilibrium flow conditions. For strongly unsteady flows, the existence of loops in both water and sediment rating curves has been demonstrated [2]. These loops are complex in nature and are likely to vary from flood to flood. In practice, loops in water and sediment rating are commonly disregarded.
Al igual que la curva de gasto caudal-altura de un solo valor (curva de gasto líquido única), la curva de gasto de sedimentos única es estrictamente válida para las condiciones de flujo estable, o flujo de equilibrio. Por otro lado, en el caso de caudales no permanentes, se ha demostrado la existencia de histéresis en ambas curvas de gasto, tanto en la de agua como la de sedimentos [2]. Estos lazos son complejos por naturaleza, y tienden a variar con la magnitud del flujo de avenida y otros factores relacionados. En la práctica, los fenómenos de histéresis en las curvas de gasto de agua y sedimentos son comúnmente ignorados.
Enrutamiento de sedimentos
El cálculo de la producción de sedimentos no proporciona una medida de la variabilidad espacial o temporal de la producción de sedimentos dentro de una cuenca. Las fórmulas de transporte de sedimentos se basan usualmente en una hipótesis de flujo estable, o permanente. Sin embargo, el término enrutamiento de sedimentos, se refiere al cálculo distribuido e inestable de la producción, transporte y deposición de sedimentos en las cuencas, arroyos, ríos, embalses y estuarios.
Por necesidad, el enrutamiento de sedimentos implica un gran número de cálculos y, por tanto, es ideal para su uso con un ordenador. El enrutamiento de sedimentos se debe utilizar, junto con las evaluaciones del rendimiento y transporte de sedimentos, en los casos en que se justifique la descripción de las variaciones espaciales y temporales del transporte de sedimentos. Los métodos de enrutamiento de sedimentos son particularmente útiles en el análisis detallado del transporte y deposición de sedimentos en cauces fluviales y embalses. Por ejemplo, el modelo HEC-RAS, o "Sistema de Análisis de Río," tiene un componente de enrutamiento de sedimentos [21]. En las últimas décadas, se han desarrollado varios otros modelos de enrutamiento de sedimentos; véase, por ejemplo, las referencias [4] y [25].
Relación de Lane
Lane [31] fue pionero en el desarrollo de la geomorfología fluvial
cuantitativa al relacionar las descargas sólida y
líquida
a la pendiente de la corriente y al diámetro medio de las partículas.
| Qs ds ∝ Qw So | (13-25) |
que establece la proporcionalidad entre el producto de la descarga de sedimentos y el diámetro de las partículas de sedimento (Qs ds) con el producto de la descarga de agua y pendiente de la corriente (Qw So). La relación de Lane es dimensional y fue derivada en base a experiencia.
Ponce [36] ha mejorado la relación de Lane, expresándola en forma adimensional de la siguiente forma:
| Qs (ds/R)1/3 ∝ γ Qw So | (13-26) |
en la cual R = radio hidráulico, y γ = peso específico del agua.
En la Ec. 13-26, Qs está dado
en unidades
La ecuación general de descarga de sedimentos por unidad de ancho es [36]:
| qs = ρ k1 v m | (13-27) |
en la cual k1 y m son coeficiente y exponente, respectivamente, de la relación de descarga de sedimentos por unidad de ancho vs velocidad media. Para el caso especial de m = 3, la Ec. 13-27 se reduce a:
en la cual k1 es adimensional.
Para m = 3, la Ec. 13-26 se reduce a la relación de transporte de sedimentos [36]:
La Ecuación 13-29 es adimensional; por lo tanto, independiente del sistema de unidades.
Aplicaciones. Asumir condiciones pre- y post-desarrollo, con subíndices 1 y 2, respectivamente.
Definir las relaciones:
a = Qs2/Qs1;
b = ds2/ds1;
c = R2/R1;
d = Qw2/Qw1; y
e = So2/So1.
De la Ecuación 13-26:
Así, el cambio de pendiente de la corriente, de pre- a post-desarrollo, es (Fig. 13-19):
qs
= ρ k1 v 3
(13-28)
Qs = 58.7 k1 γ Qw So (R/ds)1/3
(13-29)
a (b/c)1/3 = d e
(13-30)
e = (a/d) (b/c)1/3
(13-31)
Figura 13-19 Degradación del cauce aguas abajo
de la represa Fort Sumner, |
Ejemplo 13-11.
A river reach downstream of a proposed
dam has the following pre- and post-development conditions: a = 0.3, b = 1.0, c = 0.95, and d = 0.9.
Calculate the ratio of post- to pre-development stream slope.
Un tramo de río aguas abajo de una
represa proyectada
tiene las siguientes condiciones pre- y post-desarrollo: a = 0,3, b = 1,0, c = 0,95, y d = 0.9.
Calcular la relación de pendientes de pre- a post-desarrollo.
Utilizando la Ec. 13-31: e = (0,3 / 0,9) (1,0 / 0,95)1/3 = 0,34.
Esto presupone
la ausencia de control geológico, o de blindaje (armoring) de la superficie,
uno de los cuales, de estar presente, resultaría
en un aumento del valor de e por encima de 0,34.
|
13.4 DEPOSICIÓN DE SEDIMENTOS
|
|
Los conceptos de transporte y
producción de sedimentos son esenciales
para el estudio de la deposición de sedimentos.
Los sedimentos son producidos en las cuencas de cabecera
y, adicionalmente, en los canales,
y son transportados aguas abajo por
acción del agua corriente.
La deposición de sedimentos se produce en la proximidad de los embalse, típicamente como se muestra en la Fig. 13-20 [20]. En primer lugar, la deposición de las fracciones de tamaño más grueso tiene lugar cerca de la entrada al embalse. Como el agua sigue fluyendo al interior del embalse y eventualmente sobre la represa, el delta de deposición continúa creciendo en la dirección aguas abajo, hasta que llena todo el volumen disponible en el embalse. El proceso es usualmente bastante lento, pero implacable. Típicamente, los depósitos pueden tomar 50 a 100 años para llenarse, y en algunos casos, hasta 500 años o más.
Figura 15-20
Patrones longitudinales de sedimentación en un embalse |
La tasa de deposición de sedimentos en un embalse es un asunto de gran importancia económica y práctica. Los embalses son clave en los proyectos de desarrollo hidroeléctrico y de recursos hídricos. Por lo tanto, la cuestión de la vida de diseño es importante, dado que la gran mayoría de los embalses con el tiempo se llenan de sedimentos. En un ejemplo extremo, el llenado puede ocurrir en un solo evento, como en el caso de un pequeño embalse de retención de sedimentos ubicado en una región semiárida (Fig. 13-21). Por otro lado, un embalse de gran tamaño puede tomar cientos de años para llenarse, particularmente en un clima predominantemente subhúmedo o húmedo.
Figura 13-21 Embalse de retención de sedimentos
inmediatamente aguas arriba de la confluencia |
Eficiencia de retención de sedimentos en embalses
El sedimento depositado en el embalse es
la diferencia entre el sedimento entrante y el saliente.
El siguiente procedimiento se utiliza para determinar la eficiencia de retención de sedimentos en un embalse [44]:
-
Determinar la capacidad C del embalse, en hectómetros cúbicos (106 metros cúbicos) o acre-pies.
Determinar el volumen de escurrimiento medio anual I (Ingreso) al embalse, en hectómetros cúbicos (106 metros cúbicos) o acre-pies.
-
Utilizar la Fig. 13-22 para determinar la eficiencia (porcentaje de retención) como una función de la relación C/I para cualquiera de tres tamaño de sedimento: (1) grueso, (2) medio, y
(3) fino. La textura del sedimento entrante se estima mediante un estudio de las fuentes de sedimentos y/o el transporte de sedimentos por fracciones de tamaño. En la Figura 13-21, la curva superior es aplicable a sedimentos floculados y arenas gruesas; la curva media a los sedimentos que consisten de una amplia gama de tamaños de partículas; y la curva inferior, a partículas coloidales y sedimentos finos dispersados.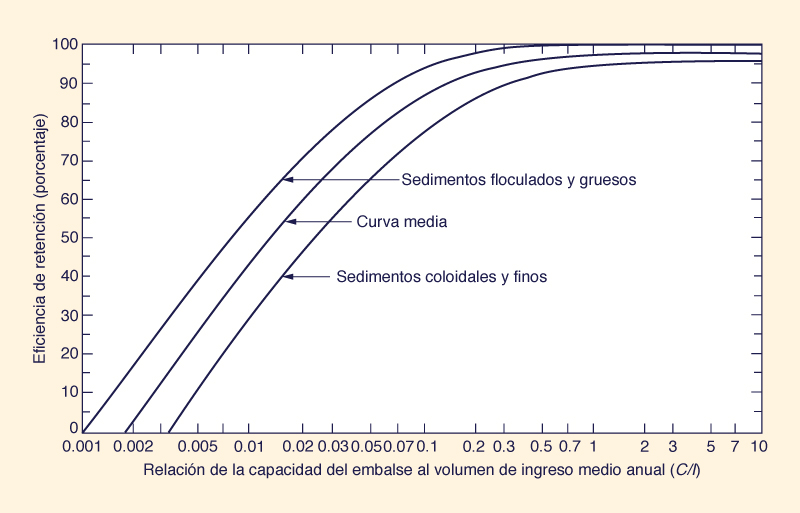
Figura 13-22 Eficiencia de retención vs relación de la capacidad del embalse
al volumen anual de escurrimento [44].
Vida útil de un embalse
La vida útil de un embalse es el período o tiempo necesario para que éste cumpla con su propósito previsto. Por ejemplo, las estructuras diseñadas por el Servicio de Conservación de Recursos Naturales (ex-Servicio de Conservación de Suelos), consideradas como parte de los programas de protección y prevención de inundaciones, tienen una vida útil de 50 a 100 años. Debido a la posible sedimentación en todos los embalses, deben tomarse las medidas apropiadas para garantizar la capacidad del embalse durante la vida util planeada. Esta consideración implica, ya sea, la limpieza de depósitos de sedimentos a intervalos predeterminados durante la vida de la estructura, o, como es usualmente el caso, el proporcionar una capacidad de almacenamiento lo suficientemente grande con el fin de almacenar todos los depósitos de sedimentos que se acumulen, sin comprometer, es decir, interferir, con el volumen de diseño del embalse. Por lo tanto, el cálculo de la tasa de acumulación de sedimentos es necesariamente parte del diseño de los proyectos de embalses.
Distribución de los sepósitos de sedimentos
La distribución de los depósitos de sedimentos
puede afectar materialmente la operación y
mantenimiento de la represas y embalses.
La cantidad y tipos de depósitos de sedimentos
varían con la naturaleza del sedimento, la forma del depósito,
la topografía (batimetría) del piso del embalse,
la naturaleza del canal de acceso, el tiempo de detención,
y la finalidad del embalse.
Figura 13-23 Deposición de sedimentos en la entrada de la represa |
Embalses de retención de sedimentos
Los embalses de retención de sedimentos, o cuencas de retención de escombros, son pequeños embalses ubicados usualmente en o cerca de zonas montañosas, con el propósito específico de atrapar sedimentos y escombros antes de que éstos puedan ser transportados y depositados en la red fluvial. Escombro es un término general utilizado para describir los adoquines, piedras, ramas y otros materiales que puedan obstruir los canales y otras estructuras hidráulicas, haciendo que lleguen a una condición crítica de diseño antes de tiempo y, algunas veces, llevando a la falla estructural.
Las cuencas de retención de escombros se colocan aguas arriba de canales o embalses, con el propósito específico de detención temporal de residuos. Las cuencas de escombros suelen ser pequeñas, y diseñadas para ser limpiadas de vez en cuando, o cuando se haga necesario. Algunas cuencas están dimensionadas para llenarse durante una o dos tormentas intensas. Otras pueden tener una vida útil de 50 ó 100 ańos. El costo del proyecto y las caracteristicas del lugar determinan el tamaño de una cuenca de retención de escombros.
Las determinaciones de producción de sedimentos para el diseño de una cuenca de retención de escombros deben considerar el análisis tanto a corto como a largo plazo. A largo plazo, la producción y entrega de sedimentos se determina a partir de una curva apropiada de gasto de sedimentos. Sin embargo, en el caso de tormentas poco frecuentes, las concentraciones actuales de sedimentos pueden resultar siendo dos a tres veces mayores que los valores medios, o normales [43].
Ejemplo 13-12.
Se planea un embalse con capacidad total de 10 hm3, con un área de drenaje de 250 km2.
El escurrimiento anual en el sitio del embalse es de 400 mm,
la producción anual de sedimentos es de 1000 toneladas/km2,
y el peso específico de los depósitos de sedimentos es de 12000 N/m3.
Un estudio en el sitio ha confirmado que los sedimentos son principalmente de grano fino.
Calcular el tiempo, en años, que tomará para que el embalse se llene con sedimentos
hasta el 80% y el 100% de su volumen original.
Los cálculos se muestran en la Tabla 13-9.
Debido a la disminución progresiva
de la capacidad del embalse con el tiempo,
se elige un intervalo de almacenamiento de ΔV = 1 hm3.
La Columna 2 muestra la pérdida de la capacidad de almacenamiento del embalse.
La Columna 3 muestra el volumen de sedimento acumulado en el embalse.
La afluencia anual media de agua al embalse, en volumen, es: 400 mm × 250 km2 = 100 hm3.
La Columna 4 muestra la relación
capacidad/entrada C/I al final de cada intervalo,
y la Columna 5 muestra el valor medio de C/I en cada intervalo.
La Columna 6 muestra la eficiencia de retención
Ti , obtenida a partir de la Fig. 13-22,
utilizando la curva de sedimentos de grano fino (curva inferior).
La afluencia anual de sedimento Is es:
1000 ton/km2/y × 1000 kg/ton × 250 km2 × 9.81 N/kg
La Columna 7 muestra el número de años que toma para llenar cada intervalo ΔV:
ΔV / [ Is (Ti / 100)].
La Columna 8 muestra que el tiempo acumulado para llenar el embalse hasta el 80% de su
capacidad es de 60 años.
Asimismo, el tiempo de llenarlo hasta el
100% de su capacidad es de 114 años.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
15.5 MEDICIONES DE SEDIMENTOS
|
|
La medición de sedimentos fluviales es a menudo necesario para complementar los estudios de transporte y rendimiento de sedimentos. La precisión de las mediciones, sin embargo, depende no solamente del equipo y las técnicas utilizadas, sino también de la aplicación de los principios básicos de transporte de sedimentos.
En cuanto los sedimentos entran en un arroyo o río, se separan en: (1) carga de material de lecho, y (2) carga de lavado. A su vez, la carga de material de lecho es transportado ya sea como: (1) carga de lecho, o (2) carga suspendida. La carga suspendida de material de lecho, más la carga de lavado, constituye el total de la carga suspendida (Fig. 13-6).
El término descarga muestreada de sedimentos suspendidos se utiliza para describir
la fracción de la carga de sedimentos suspendidos que puede ser muestreada adecuadamente con el equipo disponible.
Equipo de muemstreo de sedimentos
El equipo de muestreo de sedimentos se puede clasificar de la siguiente manera:
Muestreadores de sedimentos suspendidos, que miden la concentración de sedimentos suspendidos,
Muestreadores que miden la carga de fondo, o de lecho, y
Muestreadores de material de lecho, que muestrean el sedimento que yace en la capa superior del lecho.
Muestreadores de sedimentos suspendidos. Los muestreadores de sedimentos suspendidos se clasifican en tres tipos: (1) integradores en toda la profundidad; (2) integradores en un punto de la vertical; o (3) de muestreo en una sola profundidad. Los muestreadores integradores en la profundidad acumulan una muestra de agua y sedimento en una botella (de leche) de una pinta de tamaño (aproximadamente un litro de capacidad) a medida que se desciende el muestreador en el cauce, y se levanta luego a la superficie a una velocidad uniforme de tránsito. Estos muestreadores están diseñados de manera que la velocidad en la boquilla de admisión (al muestreador) es casi igual a la velocidad local de la corriente. Las muestras pueden ser recogidas mediante vadeo del arroyo, a mano con un soporte apropiado, o mecánicamente mediante un mecanismo de cable y carrete (Fig. 13-25).
Figura 13-25 Mecanismo de
cable y carrete, estación de aforo en el Arroyo Campo, |
El muestreador U.S. DH-48 (3.5 libras) (Fig. 13-26) es un muestreador integrador en profundidad, manual, ligero, utilizado para la colección de muestras de sedimentos suspendidos en corrientes que pueden ser vadeadas. Está diseñado para funcionar isocinéticamente, lo que significa que el agua y los sedimentos entran en la boquilla a la misma velocidad que la corriente que está siendo muestreada, con el fin de recoger una muestra representativa. Este muestreador se utiliza en los arroyos de poca profundidad, cuando el producto de la profundidad (en pies) y la velocidad media (en pies por segundo) no excede el valor de 10 [22].
Figura 13-26 Muestreador de sedimentos suspendidos integrador en la profundidad U.S. DH-48. |
Los muestreadores U.S. DH-59 y US DH-76 (22 y 25 libras, respectivamente), con suspensión de cable, se utilizan en corrientes con velocidades bajas pero con profundidades que no permiten la recolección de muestras por vadeo (Figs 13-27 y 13-28). Los muestreadores U.S. D-74 (aluminio, 42 libras; latón, 62 libras) con suspensión de cable y carrete están diseñados para su uso en corrientes que van más allá de los equipos de operación manual. Los muestreadores integradores en profundidad se han desarrollado con el fin de mejorar la precisión del muestreo y reducir el costo de la recolección de datos de sedimentos suspendidos.
Figura 13-27 Muestreador de sedimentos suspendidos integrador en la profundidad U.S. DH-59. |
Figura 13-28 Muestreador de sedimentos suspendidos integrador en la profundidad U.S. DH-76. |
Los muestreadores de integración en un punto acumulan una muestra de agua y sedimento representativa de la concentración media en cualquier punto seleccionado en una corriente, durante un corto intervalo de tiempo. Las características de admisión y escape de muestreadores de integración en un punto son idénticos a los de los muestreadores de integración en la profundidad. Una válvula rotativa que abre y cierra el muestreador es operada por un solenoide energizado por baterías en la superficie. La corriente fluye al solenoide por un cable que suspende el muestreador. Los muestreadores de integración en un punto se pueden utilizar para recoger muestras de integración en profundidad al dejar la válvula abierta mientras la toma de muestras se ejecuta a través de la vertical. Esto permite la integración en profundidad en corrientes que son demasiado profundas para ser muestreadas adecuadamente con un muestreador convencional de integración en profundidad. Los muestreadores de integración en un punto U.S. P-61-A1 (105 lb), U.S. P-63 (202 lb), y U.S. P-72 (41 lb) están en actual uso.
El muestreador de una sola etapa (single-stage sampler) se ha desarrollado para obtener datos de sedimentos suspendidos en corrientes muy repentinas, particularmente aquéllas ubicadas en zonas remotas [24]. Este muestreador se utiliza para muestreos de sedimento a una profundidad específica y sólo en la fase de subida del hidrograma. El muestreador opera sobre el principio de sifón, y por lo tanto la velocidad en la entrada no es la misma que la velocidad de la corriente. Con una operación cuidadosa, este muestreador se puede utilizar para obtener datos suplementarios sobre la concentración de sedimentos suspendidos en puntos específicos seleccionados de antemano.
Muestreadores de carga de lecho. El muestreador U.S. BLH-84
es un tipo de muestreador de carga de lecho apropriado para vadeo a mano (Fig. 13-29).
El muestreador
consiste en una boquilla de expansión,
una bolsa para contener la muestra, y una varilla pata propiciar la operación de vadeo.
Figura 13-29 Muestrador de carga de lecho U.S. BLH-84. |
El muestreador U.S. BL-84
es un muestreador de carga de lecho de operación con cable,
utilizado para recoger muestras en corrientes que no pueden ser vadeadas (Fig. 13-30).
El muestreador consta de una boquilla de
expansión montada en un marco, y una bolsa de toma de muestras.
Figura 13-30 Muestreador de carga de lecho U.S. BL-84. |
Muestreadores de material de lecho.
Los muestreadores de material
de lecho son de tres tipos:
El muestreador U.S. BMH-53 consta de
un tubo de acero inoxidable o latón
de 8 pulgadas de largo y 2 pulgadas de diámetro,
con un cilindro de corte y succión unido a una barra de control.
Figura 13-31 Muestreador de material de lecho U.S. BMH-53. |
El muestreador de material de lecho U.S. BMH-60 está diseñado para recoger una muestra de sedimento de material de lecho de aproximadamente 3 pulgadas de ancho y 2 pulgadas de profundidad. Al final de la operación de muestreo, el borde cortante se apoya contra un tope de goma, lo que evita que se pierda cualquier sedimento. El muestreador está hecho de aluminio, mide 22 pulgadas de largo y pesa 32 libras (Fig. 13-32). Se utiliza para recolectar muestras de material de lecho en corrientes con bajas velocidades pero con profundidades más allá del rango del muestreador U.S. BMH-53.
Figura 13-32 Muestreador de material de lecho U.S. BMH-60. |
El muestreador U.S. BM-54 de material de lecho (100 libras),
con suspensión de cable, es similar al muestreador U.S. BHM-60.
Este muestreador está hecho de hierro fundido, de 22 pulgadas de largo largo,
y pesa
100 libras
Figura 13-33 Muestreador de material de lecho US BM-54. |
La Tabla 13-10 provée un listado de muestreadores de sedimentos desarrollados por el Proyecto Federal Interagencial de Sedimentación (U.S. Federal Interagency Sedimentation Project).
por agencias federales de los Estados Unidos. | |||
| Tipo de sedimento | Identificación del muestreador | Peso (lbs) | Aplicable en |
| Sedimento suspendido | DH-48 | 3.5 | Velocidad × profundidad < 10 ft2/s |
| DH-59, DH-76 | 22, 25 | Arroyos mas profundas, no vadeables | |
| D-74 | 42 (aluminum); 62 (brass) | Corrientes grandes | |
| Carga de lecho | BLH-84 | 10 | Arroyos poco profundos, vadeables |
| BL-84 | 32 | Cualquier profundidad, arroyos mas profundos | |
| Material de lecho | BMH-53 | 7.5 | Arroyos poco profundos, vadeables |
| BMH-60 | 32 | Manual, baja velocidad | |
| BM-54 | 100 | Cualquier profundidad, arroyos mas profundos | |
Mediciones de sedimentos suspendidos
Las mediciones de sedimentos suspendidos se utilizan para determinar la concentración de sedimentos en un punto en una corriente (es decir, en la dirección vertical de una corriente), exceptuando una pequeña zona no medida ubicada inmediatamente encima del lecho. Con equipo de vadeo, las mediciones se pueden hacer hasta 0.3 pies del lecho. Con equipo de cable, la zona no medida varía entre 0,5 y 1,0 pies, dependiendo del tamaño del muestreador utilizado.
Suspended-sediment discharge measurements include: (1) suspended-sediment concentration, (2) particle size, (3) specific gravity, (4) temperature of water-sediment mixture, (5) water discharge, and (6) distribution of flow in the stream cross section.
Las mediciones de sedimentos en suspensión consisten de: (1) la concentración de sedimentos en suspensión, (2) el tamaño de la partícula, (3) la gravedad específica, (4) la temperatura de la mezcla agua-sedimento, (5) el caudal de agua, y (6) la distribución de flujo en la sección transversal del arroyo.
La profundidad y velocidad del flujo, y las instalaciones en el sitio de muestreo (puente, transporte por cable, etc.) tienen una influencia en la elección del muestreador. La profundidad de la corriente determina si el muestreador a ser utilizado es de operación manual (U.S. DH-48 o U.S. DH-59), o suspendido por cable (U.S. D-74). Las profundidades mayores de 15 pies requieren el uso de muestreadores en un punto, para evitar el sobrellenado de las botellas de muestreo. Cuanto más grande es el producto de la profundidad de flujo por la velocidad media, más pesada es la muestra requerida para una medida adecuada.
El número de verticales de muestreo depende de la precisión deseada y la variación de la concentración de sedimentos a través del arroyo. Para los arroyos con una sección transversal estable y concentración de sedimentos esencialmente uniforme a través del ancho, el muestreo en una sola vertical es generalmente adecuado.
Los muestreadores integradores en profundidad producen una concentración de sedimentos expresada en partes por millón, la cual puede se convertida a miligramos por litro. La descarga de sedimentos está dada por la siguiente fórmula:
| Qs = 0.0027 Cs Q | (13-33) |
en la cual Qs = descarga de sedimentos en suspensión, en toneladas por día; Cs = concentración de sedimentos en suspensión, en miligramos por litro; Q = descarga de agua, en pies cúbicos por segundo, y 0,0027 es el factor de conversión para las unidades indicadas. La Tabla 13-8 muestra el factor aplicable para convertir la concentración en partes por millón a miligramos por litro.
Hay dos maneras de medir la descarga de sedimentos en suspensión: (1) IIF, o Incrementos Iguales de Flujo, y (2) IIL, o Incrementes Iguales de Longitud. En el método IIF, el muestreo se realiza en los centroides de incrementos iguales de flujo (caudal), posisionados a través de la sección transversal. En el método IIL, el muestreo se realiza en los centroides de incrementos iguales de longitud, posisionados a través de la sección transversal.
El método IIF requiere un conocimiento de la distribución lateral del flujo antes de seleccionar las verticales de muestreo. El método IIL es aplicable a corrientes poco profundas, en las cuales la distribución del caudal en la sección transversal no es uniforme. Generalmente, el método IIL requiere menos verticales de muestreo que el método IIF. El método IIF, sin embargo, no requiere una medición previa del flujo. En el método IIF, La concentración de sedimentos en suspensión es el promedio obtenido de varias muestras integradas en profundidad. En el método IIL, la concentración de sedimentos en suspensión es la de una muestra compuesta de material, el cual abarca varias muestras integradas en profundidad.
El error en la medición de la descarga de sedimentos en suspensión varía con la profundidad de la zona no muestreada y la distribución del tamaño de los granos del sedimento suspendido. El error tiende a ser más pequeño en los casos en que el gradiente vertical de concentración en la zona no muestreada es pequeño. El gradiente de concentración cerca del lecho es pequeño para las partículas de limo y arcilla, y grande para las partículas de arena gruesa. Las correcciones en la descarga de sedimentos en suspensión, para tener en cuenta la fracción no muestreada, suelen obtenerse a través de métodos apropiados de predicción del transporte de sedimentos, tales como el método de Colby 1957 o el Método de Einstein Modificado [7, 9].
PREGUNTAS
|
|
Mencione dos definiciones alternativas de la esfericidad de una partícula de sedimento.
¿Cuál es la diferencia entre peso específico y gravedad específica?
¿Cuál es la velocidad estándar de caída? ¿Cuál es el diámetro estándar de caída?
¿Cuál es la diferencia entre la producción y la entrega de sedimentos?
Describa la diferencia entre erosión normal y erosión acelerada.
Nombre las cuatro fuentes de sedimentos.
¿Cuál es el factor de precipitacion R en la Ecuación Universal de Pérdida de Suelo?
¿Qué es la relación de entrega de sedimentos?
¿Por qué la relación de entrega de sedimentos está inversamente relacionada con el área de drenaje de la cuenca?
¿Por qué son necesarias dos fórmulas en el mátodo de Dendy y Bolton para el cálculo de la entrega de sedimentos?
Describa las dos clasificaciones de carga de sedimentos, en base a: (1) el modo predominante de transporte, y (2) si los tamaños de las partículas están representados en el lecho de la corriente.
¿Cuáles son las posibles formas de rugosidad en lechos de corrientes aluviales?
¿Cuál es el rango de aplicabilidad de la fórmula de Meyer-Peter para el transporte de carga de lecho?
¿Cuál es la diferencia básica entre los métodos Colby 1957 y Colby 1964 para el cálculo de la descarga de arenas?
¿Qué es una curva de gasto de sedimentos?
¿En que consiste el enrutamiento de sedimentos?
¿En qué consiste la eficiencia de retención de sedimento en un embalse?
¿Qué es una cuenca de retención de escombros?
Describa dos procedimientos para medir la descarga de sedimentos en suspensión.
PROBLEMAS
|
|
Calcular la velocidad de caída de una partícula de sedimento utilizando la ley de Stokes. Asumir diámetro 0,1 mm, viscosidad cinemática 1 centistoke, y gravedad específica 2.65.
Calcular el peso específico de un volumen acumulado de sedimentos en un embalse, después de un tiempo transcurrido de 100 años, en condiciones moderadas de abatimiento de la superficie del agua. Asumir la siguiente mezcla de tamaños de partículas: 55% arena, 30% limo, y 15% arcilla.
Calcular la pérdida media anual de suelo utilizando la Ecuación Universal de Pérdida de Suelo, dada una cuenca de 300 acres de extensión, cerca de Lexington, Kentucky, con las siguientes condiciones: (a) tierras de cultivo, 250 acres, contorneadas, suelo franco limoso Keen, terreno con pendiente 7% y longitud 150 pies, coeficiente C = 0,15; y (b) pastizaje, 50 acres, cobertura del dosel arbóreo 75%, cobertura del suelo con césped 60%, suelo limoso tipo Ida, terreno con pendiente 10% y longitud 200 pies.
-
Calcular la pérdida media anual de suelo utilizando la Ecuación Universal de Pérdida de Suelo para una cuenca boscosa de 1 milla cuadrada de extensión cerca de Bangor, Maine. El suelo es limo tipo Fayette, con pendiente del terreno 3% y longitud 300 pies, y el sitio está un 80% cubierto con hojarasca.
Utilice la fórmula de Dendy y Bolton para cálcular la entrega anual de sedimentos para una cuenca de 25.9 km2 de área con escurrimiento anual medio de 5 cm.
-
Determinar si una partícula de 2 mm de diámetro está en reposo bajo una profundidad de flujo de 3 m y pendiente de 0,0002. Asumir gravedad específica 2.65 y viscosidad cinemática 1 centistoke.
-
Determinar la forma de rugosidad de lecho que es probable que prevalezca bajo las siguientes condiciones de flujo: Velocidad media 3 pies/s, profundidad 8 pies, pendiente 0,0002, y diámetro de las partículas 0,3 mm.
-
Dadas las siguientes características de flujo en un canal: Profundidad 9 pies, velocidad media
3 pies/s, pendiente 0,00015, diámetro medio de las partículas 0,4 mm, y ancho medio 250 pies. Calcular la descarga de material de lecho utilizando la fórmula de Duboys. -
Dadas las siguientes características de flujo en un canal: Profundidad 3 pies, velocidad media
5 pies/s, pendiente 0.009, diámetro medio de las partículas 1 pulgada, y ancho medio 30 pies. Calcular la descarga de material de lecho (en toneladas por día) por la fórmula de Meyer-Peter. -
Dadas las siguientes características de flujo en un canal: Profundidad 5 pies, velocidad media
4 pies/s, ancho medio 180 pies, y concentración medida de la carga suspendida de material de lecho 200 ppm. Calcular la descarga total de material de lecho por el método de Colby 1957. -
Dadas las siguientes características de flujo en un canal: Profundidad 5 pies, velocidad media
3 pies/s, tamaño medio de material de lecho 0,3 mm, ancho medio 225 pies, temperatura del agua 70 °C, concentración de carga de lavado 300 ppm. Calcular la descarga de arenas por el método de Colby 1964. -
Un embalse se construirá con una capacidad de almacenamiento total de 50 hm3. La cuenca de drenaje contribuyente es de 800 kilometros2, y el escurrimiento medio anual en la zona es de 200 mm. Asuma depósitos de sedimentos bien graduados, con promedio de peso específico 1400 kg/m3. (a) ¿Cuánto tiempo tomará para que el embalse pierda 20% de su volumen? (b) ¿Cuánto tiempo tomará para que el embalse se llene completamente de sedimentos? Estimar la producción de sedimentos usando la fórmula de Dendy y Bolton.
-
Un embalse se construirá con una capacidad total de almacenamiento de 120 hm3. La cuenca de drenaje contribuyente es de 425 kilometros2, y el escurrimiento medio anual en la zona es de 45 mm. Asuma depósitos de sedimentos gruesos, con promedio de peso específico
13 kN/m3. (a) ¿Cuánto tiempo tomará para que el embalse pierda el 80% de su volumen?(b) ¿Cuánto tiempo tomará para que el embalse se llene completamente de sedimentos? Estimar la producción de sedimentos usando la fórmula de Dendy y Bolton. -
Derivar el factor de conversión 0.0027 en la Ec. 13-33.
-
Calcular la descarga de sedimentos suspendidos (en toneladas por día) para los siguientes dos casos: (1) concentración de sedimentos suspendidos 100 ppm, descarga de agua 1200 pies3/s, y (2) concentración de sedimentos suspendidos 80000 ppm, y descarga de agua 5000 pies3/s.
-
Derivar el factor de conversion de unidades C en la siguiente formula: Qs = C Cs Q, en la cual Qs está dado en kilonewtons por día, Cs en miligramos por litro, y Q en metros cúbicos por segundo.
-
Calcular la descarga de sedimentos suspendidos (en kilonewtons por día) correspondiente a una concentración de sedimentos suspendidos de 150 ppm y un flujo de 68 m3/s.
-
Calcular la descarga de sedimentos suspendidos (en kilonewtons por día) correspondiente a una concentración de sedimentos suspendidos de 22000 ppm y un flujo de 155 m3/s.
BIBLIOGRAFÍA
|
|
Ackers, P., y W. R. White. (1 973). "Sediment Transport: A New Approach and Analysis," Journal of the Hydraulics Division, ASCE, Vol. 99, No. HYll, Nov. , pp. 2041-2060.
American Society of Civil Engineers. (1975). Sedimentation Engineering, Manual No. 54.
Brown, C. B. (1950). "Sediment Transportation," Chapter XII, Engineering Hydraulics. H. Rouse, ed.. Nueva York: John Wiley.
Chang, H. H. (1988). Fluvial Processes in River Engineering. Nueva York: Wiley Interscience.
Chow, V. T. (1959). Open Channel Hydraulics. Nueva York: McGraw-Hill.
Colby, B. R., y C. H. Hembree. (1955). "Computations of Total Sediment Discharge, Niobrara River Near Cody, Nebraska," U.S. Geological Survey Water-Supply Paper 1357, Washington, D.C.
Colby, B. R. (1957). "Relations of Unmeasured Sediment Discharge to Mean Velocity," Transactions. American Geophysical Union, Vol. 38, No. 5, Washington, D.C., Oct., pp. 707-717.
Colby, B. R. (1964). "Practical Computations of Bed Material Discharge," Journal of the Hydraulics Division, ASCE, Vol. 90, No. HY2, March, pp. 217-246.
Colby, B. R. (1964). "Discharge of Sands and Mean Velocity Relations in Sand-Bed Streams," U.S. Geological Survey Professional Paper 462-A, Washington, D.C.
Collier, C. R., R. J. Pickering, and J. J. Musser. (1970). "Influences of Strip Mining on the Hydrologic Environment of Parts of Beaver Creek Basin, Kentucky, 1955-1966", U.S. Geological Survey Professional Paper 427-C, Washington, D.C.
Copper, R. H., y A. W. Peterson. (1970). Discussion of "Coordination in Mobile Bed Hydraulics," Journal of the Hydraulics Division, ASCE, Vol. 96, No. HY9, Sept., pp. 1880-1886.
Corey, A. T. (1949). "Influence of Shape on the Fall Velocity of Sand Grains," M.S. Thesis, Colorado State University, Fort Collins, Colorado.
Dendy, F. E. , y G. C. Bolton. (1976). "Sediment Yield-Runoff-Drainage Area Relationships in the United States," Journal of Soil and Water Conservation, Vol. 31, No.6, Noviembre- Diciembre, pp. 264-266.
DuBoys, P. (1879). "Le Rohne et les Rivieres a Lit Affouillable," Annales de Ponts et Chausées, Series 5, Vol. 18, pp. 141-195.
Einstein, H. A. (1950). "The Bed-Load Function for Sediment Transportation in Open Channel Flows," USDA Soil Conservation Service, Technical Bulletin No. 1026, Washington, D.C., Septiembre.
Engelund, F., y E. Hansen. (1967). "A Monograph on Sediment Transport in Alluvial Streams," Teknisk Vorlag. Copenhagen, Denmark.
Flaxman, E. M. (1972). "Predicting Sediment Yield in the Western United States," Journal of the Hydraulics Division, ASCE, Vol. 98, HY12, pp. 2073-2085.
Geiger, A. F. (1965). "Developing Sediment Storage Requirements for Upstream Retarding Reservoirs," Proceedings of Federal Interagency Sedimentation Conference, Jackson, Miss., USDA Agricultural Research Service, Miscellaneous Publication No. 970, pp. 881-885.
Guy, H. P. (1969). "Laboratory Theory and Methods for Sediment Analysis," U.S. Geological Survey, Techniques for Water Resources Investigations, Book 5, Chapter C1.
Guy, H. P. (1970). "Fluvial Sediment Concepts," U.S. Geological Survey, Techniques for Water Resources Investigations, Book 3, Chapter Cl, 1970.
Hydrologic Engineering Center, U.S. Army Corps of Engineers. (2010). "HEC-RAS, River Analysis System," Version 4.1, User's Manual, January.
Interagency Committee on Water Resources. (1952). "The Design of Improved Types of Sediment Samplers," Report No. 6. Subcommittee on Sedimentation, Federal Interagency River Basin Committee, Hydraulic Laboratory of the Iowa Institute of Hydraulic Research, Iowa City, Iowa.
Interagency Committee on Water Resources. (1957). "Some Fundamentals of Particle Size Analysis. A Study of Methods Used in Measurement and Analysis of Sediment Loads in Streams," Report No. 12. Subcommittee on Sedimentation, Saint Anthony Falls Hydraulic Laboratory, Minneapolis. Minnesota.
Interagency Committee on Water Resources. (1961). "The Single-Stage Sampler for Suspended Sediment," Report No. 13, Subcommittee on Sedimentation, Saint Anthony Falls Hydraulic Laboratory, Minneapolis, Minnesota.
Jansen, P. Ph., L. van Bendegom, J. van den Berg. M. de Vries, and A. Zanen. (1979). Principles of River Engineering. London: Pitman.
Julien, P. Y. 1995. Erosion and sedimentation. Cambridge University Press.
Kennedy, J. F. (1983). "Reflections on Rivers, Research, and Rouse." Journal of Hydraulic Engineering, ASCE, Vol. 109, No. 10, October, pp. 1254-1271.
Lane, E. W. (1947). "Report of the Subcommittee on Sediment Terminology," Transactions. American Geophysical Union, Vol. 28, No.6. December. pp. 936-938.
Lane, E. W., y V. A. Koelzer. (1953). "Density of Sediments Deposited in Reservoirs," A Study of Methods Used in Measurement and Analysis of Sediment Loads in Streams, Report No. 9, St. Paul U.S. Army Engineer District, St. Paul, Minnesota.
Lane, E. W. (1955). "Design of Stable Channels," Transactions, ASCE, Vol. 120, Paper No. 2776, pp. 1234-1279.
Lane, E. W. (1955). "The importance of fluvial morphology in hydraulic engineering," Proceedings, ASCE, Vol. 81, Paper No. 745, July, pp. 1-17.
Leifeste, D. K. (1974). "Dissolved-Solids Discharge to the Oceans from the Conterminous United States," U.S. Geological Survey Circular No. 685.
Leopold, L. B .. W. W. Emmett, y R. M. Myrick. (1966). "Channel and Hillslope Processes in a Semiarid Area in New Mexico," U.S . Geological Survey, Professional Paper No. 352-G, Washington, D.C.
McNown, J. S., y J. Malaika. (1950). "Effect of Particle Shape on Settling Velocity at Low Reynolds Number," Transactions. American Geophysical Union, Vol. 31, No.1, Feb., pp. 74-82.
Meyer-Peter, E., y R. Muller. (1948). "Formulas for Bed Load Transport," Report on Second Meeting of International Association of Hydraulic Research, Stockholm, Sweden, pp. 39-64.
Ponce, V. M. (2015). "The Lane relation revisited, with online calculation," Online article.
http://ponce.sdsu.edu/lane_relation_revisited_pubs_and_calcs.htmlRoehl, J. W. (1962). "Sediment Source Areas, Delivery Ratios, and Influencing Morphological Factors," Publication 59, International Association of Scientific Hydrology, Commission on Land Erosion, pp. 202-213.
Rouse, H. (1937). "Nomograph for the Settling Velocity of Spheres," Division of Geology and Geography, Exhibit D of the Report of the Commission on Sedimentation, 1936-1937, National Research Council, Washington, D.C., October, pp. 57-64.
Rouse, H. (1939). "An Analysis of Sediment Transportation in the Light of Fluid Turbulence," USDA Soil Conservation Service, Report No. SCS-TP-25, Washington, D.C.
Simons, D. B., y E. V. Richardson. (1966). "Resistance to Flow in Alluvial Channels," U.S. Geological Survey, Professional Paper No. 422J, Washington, D.C.
Simons, D. B., y F. Senturk. (1976). Sediment Transport Technology. Fort Collins, Colorado: Water Resources Publications.
Toffaleti, F. B. (1969). "Definitive Computation of Sand Discharge in Rivers," Journal of the Hydraulics Division, ASCE, Vol. 95, No. HY1, Jan., pp. 225-248.
U.S. Army Corps of Engineers. (1987). "Sedimentation Investigations in Rivers and Reservoirs," Engineer Manual EM 1110-2-4000, Office of the Chief of Engineers, Washington, D.C., Draft.
USDA Soil Conservation Service. (1983). National Engineering Handbook. Section 3, Sedimentation, 2d. ed., now released as Part 632.
Williams, J. R. (1975). "Sediment Yield Prediction with the Universal Soil Loss Equation Using Runoff-Energy Factor," in Present and Prospective Technology for Predicting Sediment Sources and Sediment Yields. USDA Agricultural Research Service, Publication ARS-S-40.
Wischmeier, W. H., y D. D. Smith. (1965). "Predicting Rainfall-Erosion Losses from Cropland East of the Rocky Mountains," USDA Agricultural Research Service, Agriculture Handbook No. 282 . May.
Wischmeier, W. H., C. B. Johnson, y B. V. Cross. (1971). "A Soil Erodibility Nomograph for Farmland and Construction Sites," Journal of Soil and Water Conservation, Vol. 26, No.5, Sept.-Oct.
Wolman, M. G., y A. P. Schick. (1967). "Effects of Construction on Fluvial Sediment, Urban and Suburban Areas of Maryland," Water Resources Research, Vol. 3, No.2, pp. 451-464.
Yang, C. T. (1972). "Unit Stream Power and Sediment Transport," Journal of the Hydraulics Division, ASCE, Vol. 98, No. HY10, Oct., pp. 1805-1826.
LECTURAS SUGERIDAS
American Society of Civil Engineers. (1975). Sedimentation Engineering, Manual No. 54.
Colby, B. R. (1964). "Discharge of Sands y Mean Velocity Relations in Sand-Bed Streams," U.S. Geological Survey Professional Paper 462-A, Washington, D.C.
Guy, H. P. (1970). "Fluvial Sediment Concepts," U.S. Geological Survey, Techniques for Water Resources Investigations. Book 3, Chapter C1, 1970.
U.S. Army Corps of Engineers. (1987). "Sedimentation Investigations in Rivers and Reservoirs," Engineer Manual EM 1110-2-4000, Office of the Chief of Engineers, Washington, D.C., Draft.
USDA Soil Conservation Service. (1983). National Engineering Handbook. Section 3, Sedimentation, 2d. ed., currently released as Part 632.
|
|
230522 |