[Conceptos de Estadística]   [Análisis de Frecuencia]   [Frecuencia de Flujo Bajo]   [Sequías]   [Preguntas]   [Problemas]   [Bibliografía]   •   CAPÍTULO 6:  ANÁLISIS DE FRECUENCIA  "Si se reduce la carga de sedimentos en una corriente, el equilibrio puede ser restaurado si el caudal o la pendiente se reducen, o si el diámetro de sedimentos aumenta la cantidad adecuada..." Emory W. Lane (1955) Este capítulo se divide en tres secciones. La Sección 6.1 contiene un resumen de conceptos de probabilidad y estadística útiles en la ingeniería hidrológica. La Sección 6.2 describe técnicas de analisis de frecuencia de avenidas. La Sección 6.3 trata sobre la frecuencia de flujos bajos y de seqías. 6.1  CONCEPTOS DE ESTADÍSTICA [Análisis de Frecuencia]   [Frecuencia de Flujo Bajo]   [Sequías]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   Introducción El término análisis de frecuencia se refiere a las técnicas cuyo objetivo es analizar la incidencia de las variables hidrológicas dentro de un contexto estadístico, es decir, mediante el uso de datos medidos y basando las predicciones sobre leyes estadísticas. Estas técnicas son aplicables al estudio de las propiedades estadísticas de cualquiera de las series de precipitaciones o escorrentía. En ingeniería hidrológica, sin embargo, el análisis de frecuencia es de uso común para el cálculo de los caudales de avenida. En principio, las técnicas de análisis de frecuencia son aplicables a las cuencas aforadas, con largos períodos de registro de caudales. En la práctica, estas técnicas son principalmente usadas para las cuencas grandes, ya que éstas son más propensas a ser aforadas y usualmente tienen periodos de registro más largos. El análisis de frecuencia es también aplicable a las cuencas de tamaño mediano, siempre que la longitud del registro sea adecuada. Para cuencas no aforadas (ya sea de tamaño mediano o grande), el análisis de frecuencia se puede utilizar en un contexto regional para desarrollar características de flujo aplicables a regiones hidrológicamente homogéneas. Estas técnicas comprenden lo que se conoce como análisis regional (Capítulo 7). La pregunta a responder en el análisis de frecuencia de flujo puede enunciarse de la siguiente manera: Dados n años de registros de caudales diarios de la corriente S, ¿Cuál es el flujo máximo (o mínimo) Q que es probable que se repita con una frecuencia de una vez en T años en promedio? O, cuál es el flujo máximo Q asociado con un periodo de retorno T (años)? Por otra parte, el análisis de frecuencia trata de responder a la pregunta inversa: ¿Cuál es el período de retorno T asociado con un flujo máximo (o mínimo) Q? En términos generales, las preguntas anteriores pueden expresarse de la siguiente manera: Dados n años de datos de caudal para la corriente S, y L años de vida de diseño de una determinada estructura, ¿Cuál es la probabilidad P que un caudal dado Q sea excedido por lo menos una vez durante la vida de diseño L? O dicho de otro manera, ¿Cuál es el caudal Q que tiene la probabilidad P de que sea superado durante la vida de diseño L? Variables Aleatorias El análisis de frecuencia utiliza variables aleatorias y distribuciones de probabilidades. Una variable aleatoria sigue una cierta distribución de probabilidades. Una distribución de probabilidad es una función que expresa en términos matemáticos la oportunidad relativa de ocurrencia de cada uno de todos los posibles resultados de la variable aleatoria. En la notación estadística, P (X = x1) es la probabilidad P de que la variable aleatoria X toma el resultado x1. Una notación más corta es P (x1). 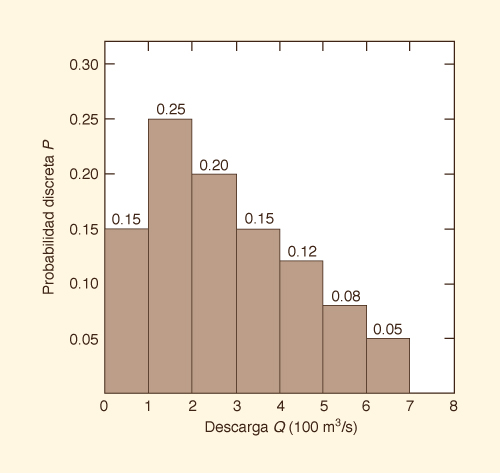La Figura 6-1 muestra un ejemplo de variable aleatoria y su respectiva distribución de probabilidades. Ésta es una distribución de probabilidad discreta porque los posibles resultados se han organizado en grupos (o clases). La variable aleatoria es la descarga Q; los posibles resultados son siete clases de descarga, de 0-100 m3/s a 600-700 m3/s. En la Fig. 6-1, la probabilidad de que Q esté en la clase 100 a 200 m3/s es 0.25. La suma de las probabilidades de todos los posibles resultados es igual a 1. Figure 6-1  Distribución de probabilidades discreta. 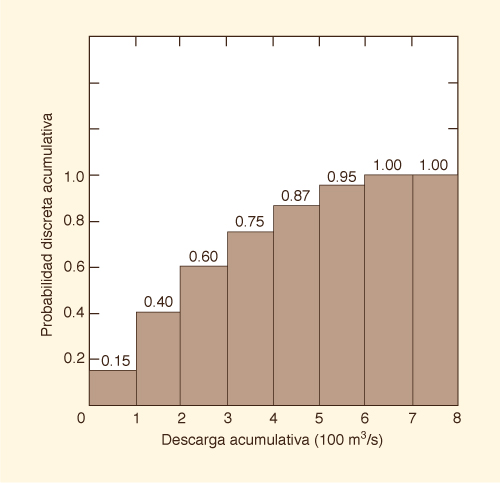La Figura 6-2 muestra una distribución discreta acumulativa, correspondiente a la distribución de probabilidades discreta de la Fig. 6-1. En esta figura, la probabilidad de que Q esté en una clase inferior o igual a la clase de 100-200 m3/s es 0.40. El valor máximo de probabilidad de la distribución acumulativa es 1. Figure 6-2  Distribución de probabilidades discreta acumulativa. ------------------------------------- STOP HERE 230812 09:45 ------------------------------------- Propiedades de Distribuciones Estadísticas Las propiedades de las distribuciones estadísticas se describen mediante las siguientes medidas: Tendencia central, Variabilidad, y Oblicuidad, o asimetría. Las distribuciones estadísticas se describen en términos de momentos. El primer momento describe la tendencia central, el segundo momento describe la variabilidad, y el tercer momento describe la asimetría. Los momentos de orden superior son posibles, pero son raramente utilizados en aplicaciones prácticas. 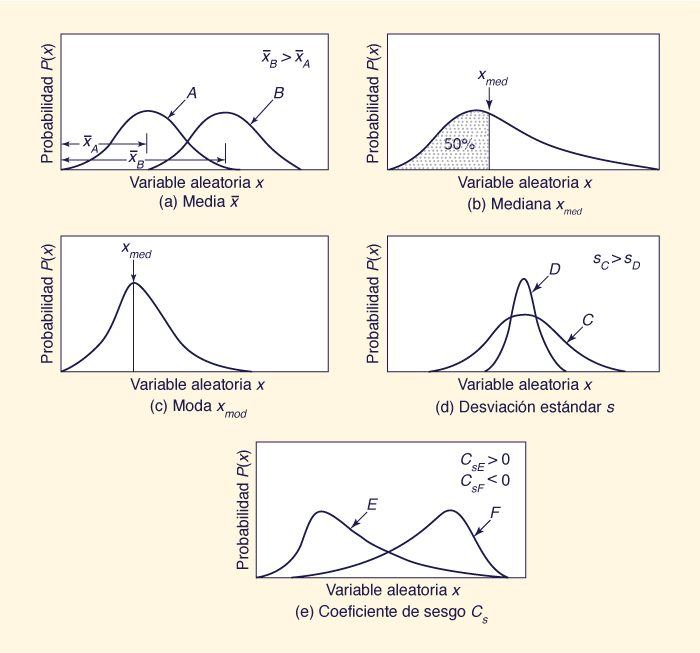El primer momento con respecto al origen es la media aritmética, o simplemente media. Ella expresa la distancia desde el origen al centroide de la distribución, como se muestra en la Fig. 6-3 (a):         1     n x̄ = ____  Σ xi         n    i =1 (6-1) en la cual x̄ es la media, xi es la variable aleatoria, y n es el número de valores. La media geométrica es la raíz enésima del producto de n términos: x̄ = (x1 x2 x3 . . . xn)1/n (6-2) El logaritmo de la media geométrica es la media de los logaritmos de los valores individuales. La media geométrica es a la distribución lognormal de probabilidades lo que la media aritmética es a la distribución normal de probabilidades. La mediana es el valor de la variable que divide a la distribución de probabilidades en dos porciones iguales (o áreas); véase la Fig. 6-3 (b). Para ciertas distribuciones asimétricas (es decir, unas con tercer momento distinto de cero), la mediana es una mejor indicación que la media de la tendencia central. Otra medida de la tendencia central es el modo, que se define como el valor de la variable que se produce con más frecuencia; véase la Fig. 6-3 (c). Fig. 6-3  Propiedades de las distribuciones estadísticas. Los momentos estadísticos se pueden definir alrededor de ejes que no sean el origen. El segundo momento respecto a la media es la varianza, definida como sigue:               1        n s 2 = ________  Σ ( xi - x̄ ) 2             n - 1    i =1 (6-3) en el cual s2 es la varianza. La raíz cuadrada de la varianza, s, es la desviación estándar. El coeficiente de varianza (o coeficiente de variación) se define como sigue:           s Cv = ____           x̄ (6-4) La desviación estándar y el coeficiente de varianza son útiles en la comparación de la variabilidad relativa entre distribuciones. Cuanto mayor sea la desviación estándar y el coeficiente de varianza, mayor es la dispersión de la distribución; véase la Fig. 6-3 (d). El tercer momento alrededor de la media es la asimetría, definido como sigue:                 n               n a = _______________  Σ ( xi - x̄ )3         (n - 1)(n - 2)     i =1 (6-5) en la cual a es la asimetría. El coeficiente de asimetría se define como sigue:            a Cs = ____           s3 (6-6) Para distribuciones simétricas, la asimetría es 0, y Cs = 0. Para la asimetría derecha (distribuciones con la larga cola a la derecha), Cs > 0; para la asimetría izquierda (larga cola a la izquierda), Cs < 0; véase la Fig. 6-3 (e). Otra medida de la asimetría es la asimetría de Pearson, definida como la relación de la diferencia entre la media y el modo, y la desviación estándar.  Ejamplo 6-1. Calcular la media, desviación estándar y coeficiente de asimetría para la siguiente serie de avenidas: 4580, 3490, 7260, 9350, 2510, 3720, 4070, 5400, 6220, 4350 y 5930 m3/s. Los cálculos se muestran en la Tabla 6-1. La Columna 1 muestra el año y la Col. 2 muestra los caudales máximos anuales. La media (Ec. 6-1) se calcula mediante la suma de Col. 2 y dividiendo la suma por n = 11. Esto resulta en x̄ = 5171 m3/s. La Columna 3 muestra las desviaciones del flujo de la media, xi - x̄. La Columna 4 muestra el cuadrado de las desviaciones de flujo, (xi - x̄ )2. La varianza (Ec. 6-3) se calcula mediante la suma de la Col. 4 y dividiendo la suma por (n - 1) = 10. Esto se traduce en: s 2 = 3,780,449 m6/ s2. La raíz cuadrada de la varianza es la desviación estándar: s = 1944 m 3/s. El coeficiente de variación (Ec. 6-4) es Cv = 0.376. La columna 5 muestra el cubo de las desviaciones de flujo, (xi - x̄)3. La asimetría (Ec. 6-5) se calcula mediante la suma de la Col. 5 y multiplicando la suma por n / [(n - 1)(n - 2)] = 11/90. Esto se traduce en a = 6,717,359,675 m9/s3. El coeficiente de asimetría (Ec. 6-6) es igual a la asimetría dividida por el cubo de la desviación estándar. Esto se traduce en Cs = 0.914. Tabla 6-1  Calcular la Media, Desviación Estándar, y Coeficiente de Asimetría:  Ejemplo 6-1. (1) (2) (3) (4) (5) Año Flujo máximo (m3/s) ( xi - x̄ ) (m3/s) ( xi - x̄ )2 (m6/s2) ( xi - x̄ )3 (m9/s3) 1 4,580 -591 349,281 -206,425,071 2 3,490 -1,681 2,825,761 -4,750,104,241 3 7,260 2,089 4,363,921 9,116,230,969 4 9,350 4,179 17,464,041 72,982,227,340 5 2,510 -2,661 7,080,921 -18,842,330,780 6 3,720 -1,451 2,105,401 -3,054,936,851 7 4,070 -1,101 1,212,201 -1,334,633,301 8 5,400 229 52,441 12,008,989 9 6,220 1,049 1,100,401 1,1515 13 4,320,649 10 4,350 -821 674,041 -553,387,661 11 5,930 759 576,081 437,245,479 Suma 56,880 37,804,491 54,960,215,521 ------------------------------------- STOP HERE 230812 18:00 ------------------------------------- Distribución de Probabilidades Contínua Una distribución de probabilidades continua se conoce como una función de densidad de probabilidades (FDP). Una FDP es una ecuación que relaciona la probabilidad, variable aleatoria, y los parámetros de la distribución. Los FDP descritos en esta sección son útiles en la ingeniería hidrológica. Distribución Normal. La distribución normal es simétrica, en forma de campana, también conocida como la distribución de Gauss, o la ley natural de errores. Tiene dos parámetros: la media μ y la desviación estándar σ de la población. En aplicaciones prácticas, la media x̄ y la desviación estándar s derivadas de datos de la muestra se sustituyen por μ y σ, respectivamente. La FDP de la distribución normal es la siguiente:                  1 f (x) = __________   e - (x - μ)2 / (2σ2)            σ (2π)1/2 (6-7) en la cual x es la variable aleatoria y f (x) es la probabilidad contínua. Por medio de la siguiente transformación:          x - μ z = ________            σ (6-8) la distribución normal se puede convertir en una distribución de un parámetro, como sigue:                 1 f (z) = ________  e-z 2/2            (2π)1/2 (6-9) en el cual z es la unidad estándar, distribuida normalmente con una media cero y una desviación estándar unitaria. De la Ecuación 6-8: x = μ + z σ (6-10) en la cual z, la unidad estándar, es el factor de frecuencia de la distribución normal. En general, el factor de frecuencia de una distribución estadística se conoce como K. Se puede derivar una función de densidad acumulativa (FDA) mediante la integración de la función de densidad de probabilidades. A partir de la Ec. 6-9, la integración conduce a lo siguiente:                  1           z F (z) = ________    ∫  e-u 2/2 du              (2π)1/2    -∞ (6-11) en la cual F(z) denota la probabilidad acumulativa, y u es una variable ficticia de integración. La distribución es simétrica con respecto al origen; por lo tanto, sólo la mitad de la distribución debe ser evaluada. La Tabla A-5 (Apéndice A) muestra los valores de F(z) versus z, en la que F(z) está integrado desde el origen hasta z.  Ejemplo 6-2. Se ha encontrado que los caudales máximos anuales de una determinada corriente están normalmente distribuidos, con una media de 90 m3/s y desviación estándar de 30 m3/s. Calcuiar la probabilidad de que ocurra un flujo mayor de 150 m3/s. Para entrar en la Tabla A-5, es necesario calcular la unidad estándar. Para un flujo de 150 m3/s, la unidad estándar (Ec. 6-8.) es: z = (150-90)/30 = 2. Esto significa que el flujo de 150 m3/s se sitúa a dos desviaciones estándar a la derecha de la media (si z hubiera sido negativo, el flujo se habría situado a la izquierda de la media). En la Tabla A-5, para z = 2, F(z) = 0.4772. Este valor mide la probabilidad acumulativa desde z = 0 a z = 2, es decir, a partir de la media (90 m3/s), hasta el valor que se considera (150 m3/s). Debido a que la distribución normal es simétrica con respecto al origen, la probabilidad acumulativa medida desde z = - ∞ hasta z = 0, es de 0.5. Por lo tanto, la probabilidad acumulativa desde z = - ∞ a z = 2, es F(z) = 0.5 + 0.4772 = 0.9772. Ésta es la probabilidad de que el flujo sea menos de 150 m3/s. Para encontrar la probabilidad de que el flujo sea mayor que 150 m3/s, se calcula la probabilidad acumulativa complementaria: G (z) = 1 - F(z) = 0.0228. Por lo tanto, hay un (0.0228 × 100) = 2.28% de probabilidad de que el flujo máximo anual sea mayor de 150 m3/s. Distribución Lognormal. Para ciertos fenómenos naturales, los valores de variables aleatorias no siguen una distribución normal, pero sus logaritmos sí lo hacen. En este caso, una FDP adecuada se puede obtener mediante el reemplazo de x por y en la ecuación de distribución normal, Ec. 6-7, en la cual y = ln (x). Los parámetros de la distribución lognormal son la media y la desviación estándar de y : μy y σy. ------------------------------------- STOP HERE 230813 06:30 ------------------------------------- Distribución Gamma. La distribución gamma se utiliza en varias aplicaciones de ingeniería hidrológica. La FDP de la distribución gamma es la siguiente:              x γ - 1 e-x/β f (x) = _____________                β γ Γ(γ) (6-12) para 0 < x < ∞, β > 0, y γ > 0. El parámetro γ se conoce como el parámetro de forma, ya que más influye en la forma de la distribución, mientras que el parámetro β se llama el parámetro de escala, ya que la mayor parte de su influencia está en el tamaño de la distribución [4]. La media de la distribución gamma es βγ, la varianza es β2γ, y la asimetría es 2/γ1/2. El término Γ(γ) = (γ - 1)! en la que γ es un número entero positivo, es una importante integral definida denominada la función gamma, definida como sigue:               ∞ Γ(γ) =   ∫ x γ - 1 e-x dx              0 (6-13) Distribuciones de Pearson. Pearson [24] ha derivado una serie de funciones de probabilidad, las cuales se adaptan virtualmente a cualquier distribución. Estas funciones han sido ampliamente utilizadas en la estadística práctica para definir la forma de varias curvas de distribución. La FDP general de las distribuciones de Pearson es la siguiente [6]:                 x                ∫   [( a + x ) / ( b0 + b1x + b2x2 )] dx               -∞ f (x) = e (6-14) en la cual a, b0, b1, y b2 son constantes. El criterio para determinar el tipo de distribución es κ, definida como sigue:                        β1( β2 + 3)2 κ = ________________________________           4 (4β2 - 3β1) (2β2 - 3β1 - 6) (6-15) en la cual β1 = μ32/μ23 y β2 = μ4/μ 22, con μ2, μ3, y μ4 siendo el segundo, tercer y cuarto momentos con respecto a la media. Con μ3 = 0 (es decir, cero asimetría), β1 = 0, κ = 0, y la distribución Pearson se reduce a la distribución normal. La distribución Pearson Tipo III ha sido ampliamente utilizada en el análisis de frecuencia de avenida. En la distribución Pearson Tipo III, κ = ∞, lo que implica que 2β2 = (3β1 + 6). Se trata de una distribución asimétrica de tres parámetros con el siguiente FDP:              (x - xo)γ - 1 e - (x - xo) /β f (x) = _________________________                         βγ Γ(γ) (6-16) y los parámetros β, γ, y xo. Para xo = 0, la distribución Pearson Tipo III se reduce a la distribución gamma (Ec. 6-12). Para γ = 1, la distribución Pearson Tipo III se reduce a la distribución exponencial, con el siguiente FDP:               1 f (x) = (____) e- (x - xo) /β               β (6-17) La media de la distribución Pearson Tipo III es xo + βγ; la varianza es β2γ; y la asimetría es 2/γ1/2. Distribuciones de Valor Extremo. Las distribuciones de valor extremo Tipos I, II, y III se basan en la teoría de valores extremos. Frechet (Tipo II) en 1927 [8] y Fisher y Tippett (Tipos I y III) en 1928 [8] estudiaron de forma independiente la distribución estadística de valores extremos. La teoría del valor extremo implica que si una variable aleatoria Q es el máximo en una muestra de tamaño n de alguna población de valores de x, entonces, siempre que n sea suficientemente grande, la distribución de Q es uno de los tres tipos asintóticos (I, II, o III), dependiendo de la distribución de x. Las distribuciones de valores extremos se pueden combinar en uno y expresarse como un valor extremo general (GEV) de distribución [23]. La función de densidad acumulada de la distribución GEV es: F ( x ) = e - [1 - k ( x - u ) / α]1/k (6-18) en la cual k, u y α son parámetros. El parámetro k define el tipo de distribución, u es un parámetro de localización, y α un parámetro de escala. Para k = 0, la distribución GEV se reduce al valor extremo Tipo I (EV1), o la distribución Gumbel. Para k < 0, la distribución GEV es la del valor extremo Tipo II (EV2), o la distribución Fréchet. Para k > 0, la distribución GEV es la del valor extremo Tipo III (EV3), o la distribución de Weibull. La distribución GEV es útil en aplicaciones en las que se está considerando una distribución de valor extremo, pero su tipo no se conoce de antemano. Gumbel [13, 14, 15, 16] ha ajustado la distribución Tipo I de valor extremo para registros largos del flujo del río de varios países. La función de densidad acumulativa (FDA) de la distribución Gumbel es la siguiente función doble exponencial: F ( x ) = e -e -y (6-19) en la cual y = (x - u)/α es la variable reducida de Gumbel. La media ȳn y desviación estándar σn de la variable Gumbel son funciones de la longitud de registro n. Los valores de ȳn y σn como una función de n se muestran en la Tabla A-8 (Apéndice A). Cuando la longitud de registro se aproxima a ∞, la media ȳn se acerca al valor de la constante de Euler (0.5772) [29], y la desviación estándar σn se acerca al valor π /61/2. El coeficiente de asimetría de la distribución de Gumbel es 1.14. La distribución de valores extremos Tipo II también se conoce como LogGumbel. Su función de densidad acumulativa es: F ( x ) = e -y 1/k (6-20) para k < 0. El valor extremo de distribución Tipo III tiene el mismo FDA que la del Tipo II, pero en este caso k > 0. Como k se aproxima a 0, las distribuciones EV2 y EV3 convergen a la distribución EV1. ------------------------------------- STOP HERE 230813 08:30 ------------------------------------- 6.2  ANÁLISIS DE FRECUENCIA [Frecuencia de Flujo Bajo]   [Sequías]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Conceptos de Estadística]   El análisis de frecuencia de avenida se refiere a la aplicación de análisis de frecuencia para estudiar la incidencia de avenidas. Históricamente, varias distribuciones de probabilidad se han utilizado para este propósito. La distribución normal fue utilizada por primera vez por Horton [19] en 1913, y poco después por Fuller [11]. Hazen [17] utilizó la distribución lognormal para reducir la asimetría, mientras que Foster [9] prefirió usar las distribuciones asimétricas de Pearson. La versión logarítmica de la distribución Tipo III de Pearson, es decir, el LogPearson III, ha sido aprobado por el Comité Consultivo Interinstitucional de EE.UU. de Datos sobre el Agua para uso general en los Estados Unidos [31]. La distribución Gumbel (valor extremo Tipo I, o EVI) también es ampliamente utilizado en los Estados Unidos y en todo el mundo. Los métodos de LogPearson III y Gumbel se describen en esta sección. Selección de Series de Datos El registro completo de caudales en una estación de aforo determinada se llama serie completa de duración . Para realizar un análisis de frecuencia de avenidas, es necesario seleccionar una serie de avenidas, es decir, una muestra de los eventos de avenidas extraídos de la serie completa de duración. Hay dos tipos de series de avenidas: (1) serie de duración parcial, y (2) serie de valores extremos. La serie de duración parcial (o picos-sobre-un-umbral (POU) [23] consta de avenidas cuya magnitud es mayor que un valor base determinado. Cuando el valor de base es tal que el número de eventos de la serie es igual al número de años de registro, la serie se llama serie de excedencia anual. En la serie de valores extremos, cada año de registro contribuye con un valor a la serie de valores extremos, ya sea el valor máximo (como en el caso del análisis de frecuencia de avenida) o el valor mínimo (como en el caso del análisis de frecuencia de flujo bajo). El primero es la serie máxima anual; y la última es la serie mínima anual. La serie anual de excedencia tiene en cuenta todos los eventos extremos por encima de cierto valor base, independientemente del momento en que ocurrieron. Sin embargo, la serie máxima anual considera sólo un evento extremo por período anual. La diferencia entre las dos series es probable que sea más marcada para los registros cortos en los que los segundos eventos anuales mayores pueden influir fuertemente en el carácter de la serie anual de excedencia. En la práctica, la serie anual de excedencia se usa para los análisis de frecuencia que implican períodos de retorno cortos, que van desde 2 a 10 años. Para períodos de retorno más largos la diferencia entre excedencia anual y serie máxima anual es pequeña. La serie máxima anual se utiliza para períodos de retorno de 10 a 100 y más. Período de Retorno, Frecuencia, y Riesgo El tiempo transcurrido entre los flujos pico sucesivos superior a un cierto flujo Q es una variable aleatoria cuyo valor medio se denomina el período de retorno T (o intervalo de recurrencia) del flujo Q. La relación entre la probabilidad y el período de retorno es el siguiente:               1 P(Q) = ____              T (6-21) en el cual P(Q) es la probabilidad de excedencia de Q, o frecuencia. Los términos frecuencia y período de retorno se usan indistintamente, aunque estrictamente hablando, la frecuencia es el recíproco del periodo de retorno. Una frecuencia de 1/T, o la frecuencia de uno en T años, corresponde a un periodo de retorno de T años. La probabilidad de no excedencia P(Q̄) es la probabilidad complementaria de la probabilidad de excedencia P(Q), definida como sigue:                                       1 P(Q̄) = 1 - P(Q) = 1  -  ____                                       T (6-22) La probabilidad de no excedencia en n años sucesivos es la siguiente:                          1      n P(Q̄) = ( 1  -  _____ )                          T (6-23) Por lo tanto, la probabilidad, o riesgo, que Q se producirá al menos una vez en n años sucesivos es:                                            1      n R = 1 - P(Q̄) = 1 - ( 1  -  _____ )                                           T (6-24) Posiciones de Ploteo Las distribuciones de frecuencias se representan (grafican) utilizando papeles de probabilidad. Una de las escalas de un papel de probabilidad es una escala de probabilidad; la otra es, o bien una escala aritmética, o una logarítmica. Las distribuciones de probabilidad normal y valor extremo son las más utilizadas en los papeles de probabilidad. ------------------------------------- STOP HERE 230813 16:10 ------------------------------------- Un papel de probabilidad aritmética tiene una escala de probabilidad normal y una escala aritmética. Este tipo de papel se utiliza para plotear las distribuciones normales y de Pearson. Un papel de probabilidad logarítmica tiene una escala de probabilidad normal y una escala logarítmica, y se utiliza para plotear distribuciones lognormal y LogPearson. Un papel de probabilidad de valor extremo tiene una escala de valor extremo, y una escala aritmética, y se utiliza para plotear las distribuciones de valores extremos. Los datos se ajustan a un ploteo de distribución normal usando una línea recta en el papel de probabilidad aritmética. Del mismo modo, los datos de un ploteo de distribución lognormal se ajustan usando una línea recta en el papel de probabilidad logarítmica, y los datos de distribución de Gumbel se ajustan usando una línea recta en el papel de probabilidad de valor extremo. Para propósitos de graficación, la probabilidad de un evento individual se puede obtener directamente de la serie de avenida. Para una serie máxima anual, se tiene la siguiente relación: x̄           m ___ = _______ N        n + 1 (6-25) en la cual x̄ = media del número de valores superados; N = número de ensayos; n = número de valores en la serie; y m = el rango de valores descendentes, con mayor igual a 1. Por ejemplo, si n = 79, el segundo mayor valor de la serie (m = 2) se superará el doble en promedio (x̄ = 2) en 80 ensayos (N = 80). Del mismo modo, el valor más grande de la serie (m = 1) se superará una vez en promedio (x̄ = 1) después de 80 ensayos (N = 80). Desde que el período de retorno T se asocia con x̄ = 1, la Ec. 6-25 se puede expresar como sigue:  1                 m ___ = P = _______  T               n + 1 (6-26) en la cual P = probabilidad de excedencia. La Ecuación 6-26 se conoce como la fórmula de posición de graficación de Weibull. Esta ecuación se utiliza comúnmente en aplicaciones hidrológicas, en particular para el cálculo de las posiciones de graficación para distribuciones no especificadas [1]. La siguiente es una fórmula general de posición de graficación [12]:  1                   m - a ___ = P = _____________  T               n + 1 - 2a (6-27) en la cual a = parámetro. Cunnane [7] realizó un estudio detallado de la exactitud de las diferentes fórmulas de posición de graficación y llegó a la conclusión de que la fórmula de Blom [3], con a = 0.375 en la Ec. 6-27, es la más apropiada para la distribución normal, mientras que la fórmula de Gringorten, con a = 0.44, debe ser usada en relación con la distribución de Gumbel. Según Cunnane, la fórmula de Weibull, para la cual a = 0, es la más apropiada para una distribución uniforme. Al calcular las posiciones de graficación, cuando el ordenamiento de valores está en orden descendente (de mayor a menor), P es la probabilidad de excedencia, o la probabilidad de que un valor sea mayor que o igual al valor indicado. Cuando el orden de los valores es en orden ascendente (de menor a mayor), P es la probabilidad de no excedencia, o la probabilidad de que un valor sea inferior o igual al valor indicado. El siguiente ejemplo muestra el cálculo de las posiciones de graficación. ------------------------------------- STOP HERE 230816 07:30 -------------------------------------  Ejemplo 6-3. Utilizar la Ecuación 6-26 para calcular las posiciones de graficación para la serie de avenidas (máxima anual) que se muestra en la Tabla 6-2, Col. 2. La solución se muestra en la Tabla 6-2, Cols. 3-5. La Columna 3 muestra los valores ordenados, de mayor a menor. La Columna 4 muestra el orden de cada valor, desde 1 a 16 (n = 16), con el valor más alto ordenado como 1 y el valor más bajo ordenado como 16. La Columna 5 muestra la probabilidad calculada por la Ec. 6-26 (expresado en porcentaje). Debido a que el ordenamiento se realizó en orden descendente, la Col. 5 muestra la probabilidad de que un valor del caudal de avenida sea mayor que o igual al valor ordenado. Para ilustrar esto, hay una probabilidad de 5.88% de que un valor de caudal de avenida sea mayor o igual a 3320 m3/s. Por el contrario, existe una probabilidad de 94.12% de que el valor del caudal de avenida sea mayor o igual a 690 m3/s. La Columna 6 muestra el período de retorno calculado por la Ec. 6-26.  Tabla 6-2   Cálculo de posiciones de graficación. (1) (2) (3) (4) (5) (6) Año Avenida Anual (m3/s) Valores ordenados (m3/s) Orden Probabilidad (porcentaje) Período de retorno (años) 1972 2520 3320 1 5.88 17.00 1973 1850 3170 2 11.76 8.50 1974 750 2520 3 17.65 5.67 1975 1100 2160 4 23.53 4.25 1976 1380 1950 5 29.41 3.40 1977 1910 1910 6 35.29 2.83 1978 3170 1850 7 41.18 2.43 1979 1200 1730 8 47.06 2.13 1980 820 1480 9 52.94 1.89 1981 690 1380 10 58.82 1.70 1982 1240 1240 11 64.71 1.55 1983 1730 1200 12 70.59 1.42 1984 1950 1100 13 76.47 1.31 1985 2160 820 14 82.35 1.21 1986 3320 750 15 88.24 1.13 1987 1480 690 16 94.12 1.06 ------------------------------------- STOP HERE 230816 08:30 ------------------------------------- Ajuste de Curvas Una vez que los datos han sido graficados en papel de probabilidades, el siguiente paso es ajustar una curva a través de los puntos graficados. El ajuste de curvas se puede lograr mediante cualquiera de los métodos siguientes: (1) método gráfico, (2) mínimos cuadrados, (3) momentos, y (4) máxima verosimilitud. El método gráfico consiste en el ajuste visual de una función a los datos. Este método, sin embargo, tiene la desventaja de que los resultados dependen en gran medida de las habilidades de la persona que realiza el ajuste. Un procedimiento más coherente es usar cualquiera de los mínimos cuadrados, momentos, o métodos de máxima verosimilitud. En el método de mínimos cuadrados, la suma de los cuadrados de las diferencias entre los datos observados y los valores ajustados se minimizan. La condición de minimización conduce a un conjunto de m ecuaciones normales, en el cual m es el número de parámetros a estimar. La solución simultánea de las ecuaciones normales conduce a los parámetros que describen el ajuste (Capítulo 7). Para aplicar el método de los momentos, es necesario primero seleccionar una distribución; a continuación, los momentos de la distribución se calculan en base a los datos. El método proporciona una conexión teórica exacta, pero la precisión se ve afectada sustancialmente por errores en la cola de la distribución (es decir, acontecimientos del período de retorno largo). Una desventaja del método es la incertidumbre en cuanto a la adecuación de la distribución de probabilidades elegida. En el método de máxima verosimilitud, los parámetros de la distribución se calculan de tal manera que el producto de las probabilidades (es decir, la probabilidad conjunta) se maximiza. Esto se obtiene de una manera similar al método de mínimos cuadrados, diferenciando parcialmente la probabilidad con respecto a cada uno de los parámetros, e igualando el resultado a cero. Los cuatro métodos de ajuste se pueden clasificar en orden ascendente de eficacia de la siguiente manera: (1) gráfico, (2) mínimos cuadrados, (3) momentos, y (4) máxima verosimilitud. Éste último, sin embargo, es algo más difícil de aplicar [6, 21]. En la práctica, el método de momentos es el más comúnmente utilizado para el ajuste de curvas; véase, por ejemplo, los métodos LogPearson III y Gumbel descritos más adelante en esta sección. ------------------------------------- STOP HERE 230816 09:30 ------------------------------------- Factores de frecuencia Cualquier valor de una variable aleatoria puede ser representado de la siguiente forma: x = x̄ + Δx (6-28) en la cual x = valor de la variable aleatoria; x̄ = media de la distribución, y Δx = desviación de la media, una función de período de retorno y las propiedades estadísticas de la distribución. La desviación de la media se puede expresar en términos del producto de la desviación estándar s y un factor de frecuencia K, de tal manera que Δx = Ks. El factor de frecuencia es una función del período de retorno y distribución de probabilidad a ser utilizada en el análisis. Por lo tanto, la Ec. 6-28 puede escribirse de la siguiente forma: x = x̄ + K s (6-29) o alternativamente, x ___ = 1 + K Cv x̄ (6-30) en el cual Cv = coeficiente de varianza. La Ecuación 6-29 fue propuesta por Chow [5] como una ecuación general para el análisis de frecuencia para uso en hidrología de avenidas. Para cualquier distribución de probabilidades, se puede determinar una relación entre el factor de frecuencia y el período de retorno. Esta relación se puede expresar en términos analíticos, en forma de tablas, o por las curvas K-T. Utilizando el procedimiento, los parámetros estadísticos se determinan primero a partir del análisis de la serie de avenidas. Para un período de retorno dado, el factor de frecuencia se determina a partir de las curvas o tablas y la magnitud de la avenida calculada por la Ec. 6-29. Método LogPearson III El método LogPearson III para análisis de frecuencia de avenidas se describe en el Boletín 17B: Directrices para la Determinación de Frecuencia del Flujo de Avenida, publicado por el Comité Consultivo Interinstitucional sobre EE.UU. sobre Datos del Agua, Reston, Virginia [31]. Metodología. Para aplicar el método, se requieren los siguientes pasos: Reunir (listar) la serie de avenida anual xi. Calcular los logaritmos de la serie anual de avenidas: yi = log xi (6-31) Calcular la media ȳ, desviación estándar sy, y coeficiente de asimetría Csy  de los logaritmos yi. Calcular los logaritmos de los caudales de avenida log Qj para cada uno de varios niveles de probabilidad seleccionados Pj, utilizando la siguiente fórmula de frecuencia: log Qj = ȳ + Kj sy (6-32) en el cual Kj es el factor de frecuencia, una función de la probabilidad Pj y el coeficiente de asimetría Csy. La Tabla A-6 (Apéndice A) muestra los factores de frecuencia K para diez niveles de probabilidad seleccionadas en el intervalo de 0.5 a 95 por ciento (y períodos de retorno correspondientes en el intervalo de 200 a 1.05 y) y los coeficientes de asimetría en el rango de -3,0 a 3.0. Calcular la descargas de avenida Qj para cada nivel de probabilidad Pj (o período de retorno Tj) mediante el cálculo de los antilogaritmos de los valores del logaritmo Qj. 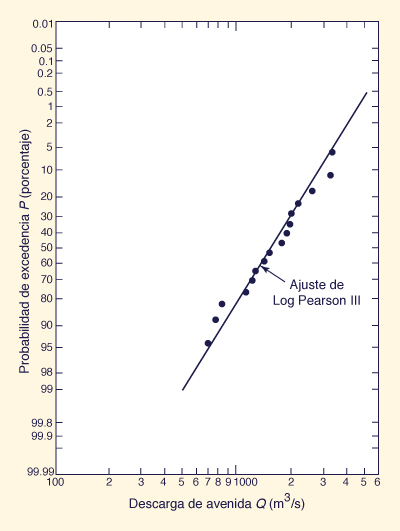Graficar los caudales de avenida Qj versus las probabilidades Pj en papel de probabilidad logarítmica, con los caudales en la escala logarítmica y las probabilidades en la escala de probabilidades. La curva LogPearson III se ajusta a los datos obtenidos mediante la unión de los puntos con una curva suave. Para Csy = 0, la curva se reduce a una línea recta. El procedimiento se ilustra mediante el siguiente ejemplo.  Ejamplo 6-4. Aplicar el método LogPearson III a la serie de avenidas del Ejemplo 6-3. Gráficar los resultados en papel de probabilidad logarítmica junto con las posiciones de ploteo calculadas en el Ejemplo 6-3. Los valores de caudales, Tabla 6-2, Col. 2, se convierten en logaritmos, y se calculan la media, la desviación estándar y el coeficiente de asimetría de los logaritmos. Esto resulta en ȳ = 3.187, sy = 0.207, and Csy = -0.116. Los cálculos se resumen en la Tabla 6-3. La Columna 1 muestran los períodos de retorno seleccionados, y la Col. 2 muestra las probabilidades asociadas en porcentaje (probabilidad de excedencia). La Columna 3 muestra los factores de frecuencia K para Csy = -0.116 para cada período de retorno o de probabilidad de excedencia. Los valores en la Columna 3 se obtienen de la Tabla A-6 por interpolación lineal. La Columna 4 muestra los logaritmos de los caudales de avenida calculados por la Ec. 6-32, y la Col. 5 muestra los caudales de avenida. Los caudales de avenida se grafican frente a las correspondientes probabilidades, como se muestra por la línea continua de la Fig. 6-4, para obtener el ajuste LogPearson III a los datos. Las posiciones de ploteo calculadas en el Ejemplo 6-3 se muestran también para comparación.  Table 6-3  Método Log Pearson III:  Ejemplo 6-4. (1) (2) (3) (4) (5) Período de retornoT (y) Probabilidad P (percent) Factor de frecuencia K (para Csy = - 0.116) yi = log Q Q (m3/s) 1.05 95 -1.677 2.840 692 1.11 90 -1.293 2.919 830 1.25 80 -0.835 3.014 1033 2 50 0.019 3.191 1552 5 20 0.847 3.362 2301 10 10 1.268 3.449 2812 25 4 1.710 3.541 3475 50 2 1.991 3.599 3972 100 1 2.240 3.651 4477 200 0.5 2.467 3.698 4989   CÁLCULO EN LÍNEA. Utilizando ONLINE PEARSON, los resultados son esencialmente los mismos, variando de Q = 691 m3/s para T = 1.05 años, a Q = 4984 m3/s para T = 200 años. Figure 6-4  LogPearson III:  Ejemplo 6-4 [31]. ------------------------------------- STOP HERE 230820 19:30 ------------------------------------- Coeficiente de Asimetría Regional El coeficiente de asimetría de la serie de avenidas (es decir, la asimetría de la estación hidrométrica) es sensible a los fenómenos extremos. La precisión global del método puede ser mejorada mediante el uso de un valor ponderado de asimetría en lugar del valor de la estación. En primer lugar, se obtiene un valor de asimetría regional, y la asimetría ponderada se calcula ponderando las asimetrías regionales en proporción inversa a sus errores cuadráticos medios (MSE). La fórmula para la asimetría ponderada es la siguiente:               (MSE)sr Csy  +  (MSE)sy Csr Csw = ________________________________                     (MSE)sr + (MSE)sy (6-33) en el cual Csw = asimetría ponderada; Csy = asimetría de la estación; Csr = asimetría regional; (MSE)sy = error del mínimo cuadrado de la asimetría regional. Para desarrollar un valor de asimetría regional, es necesario reunir datos de al menos 40 estaciones o, en su defecto, todas las estaciones dentro de un radio de 160 km. Las estaciones deben tener al menos 25 años de registro. En ciertos casos, la escasez de datos puede requerir una relajación de estos criterios. El procedimiento incluye el análisis por tres métodos: (1) mapa de isolíneas asimétricas, (2) ecuación de predicción de asimetría, y (3) parámetros estadísticos de la estación asimétrica. Para desarrollar un mapa de isolíneas asimétricas, la asimetría de cada estación se grafica, en un mapa, en el centro de gravedad de su área de cuenca, y los datos graficados se examinan para identificar cualquier tendencia geográfica o topográfica. Si se evidencia un patrón, las isolíneas (líneas de igual asimetría) se dibujan y se calcula el MSE. El MSE es la media de los cuadrados de las diferencias entre las asimetrias observadas y las asimetrías de las isolíneas. Si no hay un patrón evidente, un mapa de isolíneas no puede desarrollarse, y este método se rechaza. En el segundo método, una ecuación de predicción se utiliza para relacionar la asimetría de la estación a las propiedades de la cuenca y las variables climatológicas. El MSE es la media de los cuadrados de las diferencias entre las asimetrías observadas y pronosticadas. En el tercer método, la media y la varianza de las asimwtrías de estación se calculan. En algunos casos, la variabilidad de la escorrentía puede ser tal que todas las estaciones pueden no ser hidrológicamente homogénea. Si este es el caso, los valores de alrededor de veinte (20) estaciones se pueden utilizar para calcular la media y la varianza de los datos. De los tres métodos, se selecciona el que proporciona la estimación más precisa del coeficiente de asimetría. En primer lugar, se efectúa una comparación de las MSE del mapa de isolíneas y se formulan ecuaciones de predicción. A continuación, el MSE más pequeño se compara con la varianza de los datos. Si el MSE más pequeño es significativamente menor que la varianza, aquél debe ser usado en la Ecuación 6-33 como (MSE)sr. Si éste no es el caso, se debe utilizar la varianza como (MSE)sr, usándose la media de la asimetría de la estación como asimetría regional (CSR). 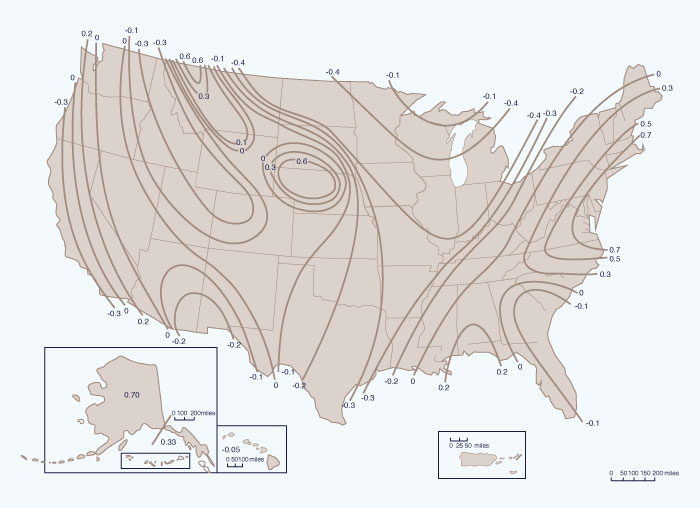En ausencia de estudios regionales de asimetría, los valores generalizados de asimetría regional para su uso en la Ec. 6-33 se pueden obtener de la Fig. 6-5. Cuando la inclinación regional se obtiene de esta figura, el error cuadrático medio de la asimetría regional es MSEsr = 0.302. El error cuadrático medio de la asimetría de la estación se aproxima mediante la siguiente fórmula: (MSE)sy = 10 A - B log (n/10) (6-34) en la cual A = - 0.33 + 0.08G,     para G < 0.9 (6-34a) A = 0.52 + 0.30G,      para G ≥ 0.9 (6-34b) B = 0.94 - 0.26G,       para G < 1.5 (6-34c) B = 0.55,                     for G ≥ 1.5 (6-34d) en las cuales G = valor absoluto de la asimetría de la estación, y n = longitud de los datos, en años. Figura 6-5  Coeficientes de asimetría generalizados de los logaritmos del caudal máximo anual [31] (Haga Click -aquí- para desplegar). ------------------------------------- STOP HERE 230821 09:15 -------------------------------------  Ejemplo 6-5. Una estación en San Diego, California, cuenta con registros de avenida de 34 años, con asimetría de la estación Csy = - 0.1. Calcular la asimetría ponderada siguiendo la Ec. 6-33 y Fig. 6-5. De la Fig. 6-5, el valor generalizado de la asimetría regional es Csr = -0.3. El MSE de la asimetría de la estación se calcula con la Ec. 6-34, con G = 0.1: (MSE)sy = 0.156. Por lo tanto, la asimetría ponderada es (Ec. 6-33.): Csw = - 0.168. Tratamiento de valores extremos. Los valores extremos son los datos individuales que se apartan significativamente de la tendencia general. El tratamiento de estos valores extremos (es decir, su retención, modificación o supresión) puede tener un efecto importante en el valor de los parámetros estadísticos calculados a partir de los datos, en particular para muestras pequeñas. Los procedimientos para el tratamiento de valores extremos, invariablemente, requieren de un juicio que involucra consideraciones matemáticas e hidrológicas. La detección y el tratamiento de valores extremos altos y bajos en el método del LogPearson III se lleva a cabo de la siguiente manera [31]. Para asimetría de estación superior a +0.4, las pruebas para valores extremos altos se consideran en primer lugar. Para asimetría de estación menor que -0.4, las pruebas de valores extremos bajos se consideran en primer lugar. Para asimetría de estación en el rango de -0.4 a +0.4, las pruebas para valores extremos altos y bajos se consideran simultáneamente, sin eliminar valores extremos de los datos. La siguiente ecuación se usa para detectar valores extremos altos: yH = ȳ + Kn sy (6-35) en el cual yH = límites de valores extremos altos (en unidades logarítmicas); y Kn = factor de frecuencia de valores extremos, una función de la longitud de registro n. Los valores de yH se dan en la Tabla A-7 (Apéndice A). Los valores de yi (logaritmos de la serie de avenidas) mayores que yH se consideran altos valores extremos. Si hay evidencia suficiente para indicar que un alto valor extremo es un máximo en un periodo de tiempo prolongado, se trata es dato como dato históricos. De lo contrario, se retiene como parte de la serie de avenidas. Los datos históricos se refiere a la información de avenida fuera de la serie de avenidas, que se puede utilizar para extender el registro a un período mucho más largo que el de la serie de avenida. El conocimiento histórico se utiliza para definir el período histórico H, que es más largo que el período de registro n. Al número z de eventos que son conocidos por ser los más grandes en el período histórico se les da un peso de 1. Los n eventos restantes de la serie de avenidas se les da un peso de (H - z)/n. Por ejemplo, para una longitud de registro n = 44 años, un período histórico H = 77 años, y un número de picos en el período histórico z = 3, el peso aplicado a los tres picos históricos sería 1, y el peso aplicado a la serie de avenidas restante sería (77 - 3) / 44 = 1.68. En otras palabras, el registro se amplía a 77 años, y los 44 años de la serie de avenidas (excluyendo los valores extremos que se han considerado parte de los datos históricos) representan 74 años de los datos en el período histórico de 77 años [31]. La siguiente ecuación se utiliza para detectar valores extremos bajos: yL = ȳ - Kn sy (6-36) en el cual yL = límite de los valores extremos bajos (en unidades logarítmicas) y los otros términos son los definidos previamente. Si un ajuste para los datos históricos se ha hecho anteriormente, los valores en el lado derecho de la Ec. 6-36 son los utilizados previamente en el cálculo históricamente ponderado. Los valores de yi más pequeños que yL se consideran valores extremos bajos y son borrados de la serie de avenidas [31]. Complementos de las estimaciones de frecuencia de avenidas. La precisión de las estimaciones de avenidas basado en el análisis de frecuencia se deteriora para valores de probabilidad mucho mayor que la longitud de registro. Esto es debido al error de muestreo y al hecho de que la distribución subyacente no se conoce con certeza. Se recomiendan los procedimientos alternativos que complementan la información proporcionada por el análisis de frecuencia de avenidas. Estos procedimientos incluyen las estimaciones de avenida de los datos de precipitación (por ejemplo, el hidrograma unitario, Capítulo 5) y la comparación con las cuencas de características hidrológicas similares (el análisis regional, Capítulo 7). La Tabla 6-4 muestra la relación entre los diversos tipos de análisis utilizados en los estudios de frecuencia de avenidas.  Table 6-4   Tipos de análisis usados en los estudios de frecuencia de avenidas [31]. Descripción Longitud del registro n (años) 10 - 24 25 - 49 ≥ 50 Análisis estadístico de frecuencia de avenidas ✓ ✓ ✓ Comparaciones con cuencas similares ✓ ✓ - Estimación de avenidas en base a precipitación ✓ - - ------------------------------------- STOP HERE 230821 18:00 ------------------------------------- Método de Valor Extremo de Gumbel Tipo I La distribución de valor extremo Tipo I, también conocida como el método de Gumbel [16], o EV1, ha sido ampliamente utilizado en los Estados Unidos y otros países. El método es un caso especial de la distribución GEV de tres parámetros descritos en el Reporte Británico de Estudios de Avenidas [23]. La función de densidad acumulativa F(x) del método de Gumbel es el doble exponencial, Ec. 6-19, repetida aquí por conveniencia: F(x) = e -e -y (6-19) en la cual F(x) es la probabilidad de no excedencia. En el análisis de frecuencia de avenidas, la probabilidad de interés es la probabilidad de excedencia, es decir, la probabilidad complementaria a F(x): G(x ) = 1 - F(x ) (6-37) El período de retorno T es la inversa de la probabilidad de excedencia. Por lo tanto,    1 _____ = 1 - e -e -y   T (6-38) De la Ec. 6-38:                      T y = - ln ln  _______                   T - 1 (6-39) En el método de Gumbel, los valores de caudales de avenida se obtienen de la fórmula de frecuencia, Ec. 6-29, que se repite aquí por conveniencia: x = x̄ + K s (6-29) El factor de frecuencia K se evalúa con la fórmula de frecuencia: y = ȳn + K σn (6-40) en la cual y = variable (reducida) de Gumbel, una función del período de retorno (Ec. 6-39.); y ȳn y σn son la media y la desviación estándar de la variable de Gumbel, respectivamente. Estos valores son una función de la longitud de registro n (véase Table A-8, Apéndice A). En la Ec. 6-29, para K = 0, x es igual a la media de la avenida anual x̄. Del mismo modo, en la Ec. 6-40, para K = 0, la variable de Gumbel y es igual a su media ȳn. El valor límite de ȳn, para n → ∞ es la constante de Euler, 0.5772 [28]. En la Ec. 6-38, para y = 0.5772: T = 2.33 años. Por lo tanto, el período de retorno de 2.33 años se toma como el período de retorno de la avenida media anual. De las Ecs. 6-29 y 6-40:                   y  -  ȳn x = x̄  +  ___________ s                      σn (6-41) y con la Ec. 6-39:                   ln ln [T / (T - 1)]  +  ȳn x = x̄  -  __________________________ s                                   σn (6-42) Los pasos siguientes son necesarios para aplicar el Método de Gumbel: Ensamblar la serie de avenidas. Calcular la media x̄ y la desviación estándar s de la serie de avenidas. Utilizar la Tabla A-8 para determinar la media ȳn y la desviación estándar σn de la variable de Gumbel como una función de la longitud de registro n. Seleccionar varios períodos de retorno Tj  y probabilidades de excedencia asociados Pj. Calcular las variables de Gumbel yj correspondientes a los períodos de retorno Tj  por medio de la Ec. 6-39, y calcular el caudal Qj = xj para cada variable de Gumbel (y el periodo de retorno asociado) usando la Ec. 6-41. Alternativamente, los caudales de avenida se pueden calcular directamente para cada periodo de retorno mediante el uso de la Ec. 6-42. Los valores de Q se plotean frente a y o T (o P) sobre papel de probabilidad de Gumbel, y una línea recta se dibuja a través de los puntos. El papel de probabilidad de Gumbel tiene una escala aritmética de variables de Gumbel y en las abscisas y una escala aritmética de la descarga de avenida Q en las ordenadas. Para facilitar la lectura de las frecuencias y probabilidades, la Eq. 6-38 puede utilizarse para superponer una escala de período de retorno T (o probabilidad P) en la escala aritmética de la variable de Gumbel y.  Ejamplo 6-6. Aplicar el método de Gumbel a la serie de avenida del Ejemplo 6-3. Graficar los resultados sobre el papel de Gumbel junto con las posiciones del ploteo calculadas en el Ejemplo 6-3. La media y la desviación estándar de las series de avenida son: x̄ = 1704 m3/s and s = 795 m3/s. A partir de la Tabla A-8. para n = 16, la media y la desviación estándar de la variable de Gumbel son ȳ = 0.5157 and σn = 1.0316. Los resultados se muestran en la Tabla 6-5. Las Columnas 1 y 2 muestran períodos de retorno seleccionados T y las probabilidades de excedencia asociados (en porcentaje). La Columna 3 muestra los valores de la variable de Gumbel calculados por la Ec. 6-39. La Columna 4 muestra el caudal de avenida Q calculado por la Ec. 6-41 para cada variable y, período de retorno T, y probabilidad de excedencia asociada P. 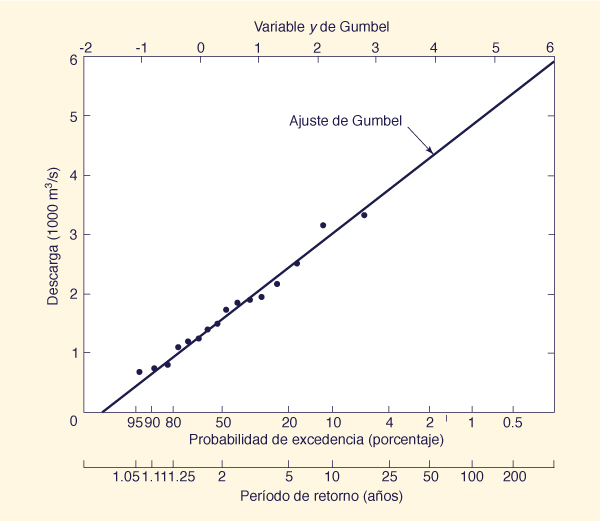Los caudales de avenida definen una línea recta cuando se representan gráficamente versus al período de retorno en papel de Gumbel, como muestra la línea continua de la Fig. 6-6. Las posiciones gráficas calculadas en el Ejemplo 6-3 se muestran para propósitos de comparación.  Tabla 6-5  Método Gumbel:  Ejemplo 6-6. (1) (2) (3) (4) Período de retorno T (y) Probabilidad P (porcentaje) Variable de Gumbel y Caudal de avenida Q (m3/s) 1.05 95 - 1.113 449 1.11 90 - 0.838 661 1.25 80 - 0.476 940 2 50 0.367 1590 5 20 1.500 2462 10 10 2.250 3040 25 4 3.199 3772 50 2 3.902 4314 100 1 4.600 4851 200 0.5 5.296 5388   CÁLCULO EN LÍNEA. Utilizando ONLINE GUMBEL, el resultado es esencialmente el mismo, variando de Q = 447 m3/s para T = 1.05 años, a Q = 5396 m3/s para T = 200 años. Figure 6-6   Análisis de frecuencia de avenidas por el Método de Gumbel:   Ejemplo 6-6. Modificaciones al método de Gumbel. Desde sus inicios en la década de 1940, se han propuesto varias modificaciones al método de Gumbel. Gringorten [12] ha demostrado que la distribución de Gumbel no sigue la regla de graficación de Weibull, la Ec. 6- 26 (o la Ec. 6-27 con a = 0). Se recomienda a = 0.44, lo que llevó a la fórmula de posición del graficación de Gringorten:   1                     m  -  0.44 ____  =  P  =  _______________   T                     n  +  0.12 (6-43) Lettenmaier y Burges [22] han sugerido que una mejor estimación de la avenida se obtiene mediante el uso de los valores límite de la media y la desviación estándar de la variable de Gumbel (es decir, los correspondientes a n = ∞) en la Eq. 6-40, en lugar de basar estos valores en la longitud de registro. En este caso, ȳn = 0.5772, y σn = π / 61/2 = 1.2825. Por lo tanto, la Ec. 6-41 se reduce a lo siguiente: x = x̄  +  (0.78 y  -  0.45) s (6-44) y la Ec. 6-42 se reduce a:                                    T x = x̄  +  (0.78 ln ln _______  +  0.45) s                                 T - 1 (6-45) Lettenmaier y Burges [22] también han sugerido que una estimación de la varianza, usando n como el divisor en la Ec. 6-3, proporciona mejores cálculos de los eventos extremos que la estimación de costumbre, es decir, usando el divisor n - 1. Comparison Between Flood Frequency Methods Comparación entre los Métodos de Frecuencia de Avenida En 1966, el Subcomité de Hidrología del Consejo de Recursos Hídricos de EE.UU. comenzó a trabajar en la selección de un método adecuado de análisis de frecuencia de avenida que podría recomendarse para uso general en los Estados Unidos. El comité puso a prueba la bondad de ajuste de seis distribuciones: (1) lognormal, (2) LogPearson III, (3) Hazen, (4) gamma, (5) Gumbel (EV1) y (6) logGumbel (EV2). El estudio incluyó a diez conjuntos de registros, el menor de los cuales era 40 años. Los resultados mostraron que las tres primeras distribuciones tenían desviaciones medias más pequeñas que las tres últimas. Dado que la distribución de Hazen es un tipo de distribución logarítmica normal y el logaritmo normal es un caso especial de LogPearson III, el Comité llegó a la conclusión de que este último era el más apropiado de los tres, y por lo tanto recomienda su uso general. El mismo tipo de análisis se repitió para los seis conjuntos de registros en el Reino Unido, el menor de los cuales era de 32 años [2]. Los métodos fueron: (1) gamma, (2) log gamma, (3) lognormal, (4) Gumbel (EV1), (5) GEV, (6) Pearson III y LogPearson III. En períodos de retorno bajos (de 2 a 5 años), el GEV y Pearson III mostraron las desviaciones medias más pequeños, mientras que para los períodos de retorno superiores a 10 años el método de Log Pearson III tenía las desviaciones medias más pequeñas. Estudios comparativos similares se hicieron en el Informe Británico de Estudios de Avenida [23]. El estudio concluyó que las distribuciones de tres parámetros (GEV, Pearson III, y LogPearson III) proporcionan un mejor ajuste que las distribuciones de dos parámetros (Gumbel, lognormal, gamma, y log gamma). Sobre la base de criterios de la desviación absoluta media, el estudio concluyó que el método de LogPearson III es mejor que el GEV, y éste último mejor que el Pearson III. Sin embargo, basado en la raíz de la desviación cuadrática media, calificó el Pearson III mejor que las distribuciones LogPearson III y GEV. Aunque, en general, los métodos de tres parámetros parecen ser mejores que los métodos de dos parámetros, estos últimos no deben ser completamente descartados. El Informe Británico de Estudios de Avenida [23] observó que su uso en conexión con longitudes de registro cortos a menudo conduce a resultados que son más sensibles que los obtenidos por las distribuciones de tres parámetros. Una distribución de tres parámetros usado con una muestra pequeña puede en algunos casos implicar que existe un límite superior al caudal de avenida igual a aproximadamente el doble de la avenida anual media. Si bien puede haber un límite superior a la magnitud de las avenidas, sin duda es mayor que el doble de la avenida media anual. ------------------------------------- STOP HERE 230822 16:00 ------------------------------------- 6.3  FRECUENCIA DE FLUJO BAJO [Sequías]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Conceptos de Estadística]   [Análisis de Frecuencia]   Mientras que los flujos altos conducen a avenidas, los flujos bajos sostenidos pueden dar lugar a sequías. Una sequía se define como la falta de lluvia tan grande y continua que pueda afectar a la vida animal y vegetal de una región de manera adversa, y agotar los suministros de agua doméstica e industrial, especialmente en aquellas regiones en las cuales la lluvia es normalmente suficiente para tales fines [18]. En la práctica, una sequía se refiere a un período de suministros inusualmente bajos de agua, independientemente de la demanda de agua. Las regiones más afectadas por la sequía son las que tienen mayor variabilidad en las precipitaciones anuales. Estudios han demostrado que las regiones para las cuales el coeficiente de varianza de la precipitación anual excede 0.35 son más propensas a frecuentes sequías [6]. La variabilidad de la precipitación anual baja y la precipitación anual alta son típicas de las regiones áridas y semiáridas. Por lo tanto, estas regiones son más propensas a las sequías. Los estudios de anillos de árboles, que documentan las tendencias a largo plazo de las precipitaciones, muestran patrones claros de períodos de clima húmedo y seco [30]. Si bien no hay una explicación evidente para los ciclos de clima húmedo y seco, los años secos se deben considerar en la planificación de proyectos de recursos hídricos. El análisis de los registros de tiempo ha demostrado que existe una tendencia a que los años secos se agrupen. Esto indica que la secuencia de años secos no es al azar, pues los años secos tienden a seguir a otros años secos. Por lo tanto, es necesario tener en cuenta tanto la severidad y la duración de un período de sequía. La severidad de sequías se puede establecer mediante la medición de los siguientes factores: Deficiencia en la precipitación y escorrentía, Disminución de la humedad del suelo, y/o Disminución de los niveles de agua subterránea. Por otra parte, el análisis de frecuencia de flujo bajo se puede utilizar en la evaluación de la probabilidad de ocurrencia de sequías de diferentes duraciones. 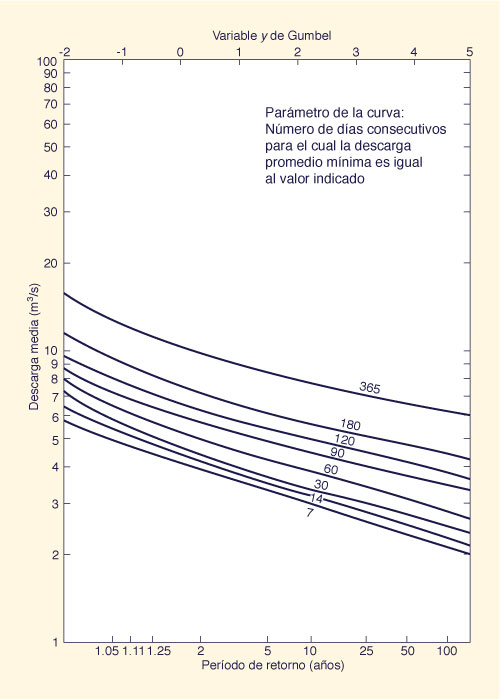Figura 6-7  Curvas de frecuencia de flujo bajo [28]. Los métodos de análisis de frecuencia de flujo bajo se basan en la hipótesis de invariabilidad de las condiciones meteorológicas. La ausencia de registros de tiempo, sin embargo, impone una estricta limitación al análisis de frecuencia de bajo flujo. Cuando registros de suficiente longitud están disponibles, el análisis comienza con la identificación de la serie de flujo bajo; se utilizan ya sea los mínimos anuales o la serie de excedencia anual. En un análisis mensual, la serie mínima anual está formada por los volúmenes de los flujos mensuales más bajos de cada año de registro. Si se elige el método de excedencia anual, los volúmenes de flujo mensual más bajo en el registro se seleccionan, independientemente del momento en que ocurrieron. En el último método, el número de valores en la serie no tiene que ser igual al número de años de registro. Una curva de duración de flujo puede ser usada para dar una indicación de la severidad de los flujos bajos. Esta curva, sin embargo, no contiene información sobre la secuencia de flujos bajos o la duración de posibles sequías. El análisis se hace más significativo mediante la abstracción de los flujos mínimos durante un período de varios días consecutivos. Por ejemplo, para cada año, el período de 7 días con un volumen de flujo mínimo se abstrae, y el flujo mínimo es el flujo promedio para ese período. Un análisis de frecuencia en la serie de flujos bajos, utilizando el método de Gumbel, por ejemplo, resulta en una función que describe la probabilidad de ocurrencia de los flujos bajos de una cierta duración. El mismo análisis repetido para otras duraciones, conduce a una familia de curvas que representan la frecuencia de bajo flujos bajos, como se muestra en la Fig. 6-7 [28]. En el diseño de embalses, la evaluación de flujos bajos es ayudada por una curva de flujo de masa. La técnica consiste en la determinación de los volúmenes de almacenamiento necesarios para todos los períodos de flujo bajo. A pesar de que es prácticamente imposible proporcionar almacenamiento suficiente para satisfacer los riesgos hidrológicos de muy poca frecuencia, una práctica común consiste en preveer un riesgo indicado (es decir, una probabilidad de sequía) y añadir un porcentaje adecuado del volumen de almacenamiento calculado, como margen de almacenamiento de reserva. El coeficiente de variación de los flujos anuales se utiliza en la determinación de los niveles de riesgo y tolerancia de almacenamiento. Los niveles extraordinarios de sequía se alcanzan a continuación mediante la reducción de las tasas de aprovechamiento de los proyectos. Los ríos regulados pueden alterar las condiciones de flujo natural para proporcionar un flujo mínimo aguas abajo para fines específicos. En este caso, los embalses sirven como el mecanismo para difusionar la variabilidad del flujo natural en los flujos de aguas abajo, los cuales se pueden hacer esencialmente constantes en el tiempo. La regulación es necesaria para el mantenimiento de flujos bajos, con el propósito de cumplir con demandas de agua para la agricultura, demanda municipal e industrial, flujos ecológicos mínimos, navegación, y la regulación del control de calidad del agua. ------------------------------------- STOP HERE 230825 17:00 ------------------------------------- 6.4  SEQUÍAS [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Conceptos de Estadística]   [Análisis de Frecuencia]   [Frecuencia de Flujo Bajo]   La sequía es un fenómeno natural relacionado con el clima, que afecta a las varias regiones de la Tierra durante meses o años. Tiene un impacto en la producción de alimentos, la reducción de la esperanza de vida y el rendimiento económico de las grandes regiones geográficas, o países enteros. La sequía es un rasgo recurrente del clima; se produce en prácticamente todas las zonas climáticas, y sus características varian considerablemente entre regiones. La sequía difiere de la aridez en que la sequía es temporal; aridez es una característica permanente de regiones con escasez de precipitaciones. La sequía está relacionada con una deficiencia de precipitación durante un período prolongado de tiempo, por lo general una temporada o más (Fig. 6-8). Esta deficiencia da lugar a una escasez de agua para alguna actividad, grupo o sector ambiental. La sequía también está relacionada con la distribución temporal de precipitación. Otros factores climáticos tales como alta temperatura, vientos fuertes, y baja humedad relativa están a menudo asociados con sequía. La sequía es más que un fenómeno físico o evento natural. Su impacto resulta de la relación entre un evento natural y las demandas en el suministro de agua, lo cual a menudo se ve agravado por las actividades humanas. La experiencia con sequías ha puesto de relieve la vulnerabilidad de las sociedades humanas a este peligro natural. Figura 6-8  Desierto de Río Grande do Norte, en la región semiárida del Noreste del Brasil. ------------------------------------- STOP HERE 230829 14:00 ------------------------------------- Definiciones de sequía Las definiciones de sequía son de dos tipos: (1) conceptuales, y (2) operacionales. Las definiciones conceptuales ayudan a entender el significado de sequía y sus efectos. Por ejemplo, la sequía es un período prolongado de deficiencia de precipitación que causa grandes daños a los cultivos, lo que resulta en la pérdida de productividad. Las definiciones operacionales ayudan a identificar el principio de la sequía, el fin y el grado de severidad. Para determinar el inicio de la sequía, las definiciones operacionales especifican el grado de desviación de la media de la precipitación en un cierto período de tiempo. Esto generalmente se logra mediante la comparación de la situación actual (el período de estudio) con el promedio histórico. El umbral identificado como el comienzo de una sequía (por ejemplo, 75% de la precipitación media durante un período de tiempo especificado) generalmente se establece en forma un tanto arbitraria. Una definición operacional para la agricultura puede comparar la precipitación diaria y la evapotranspiración para determinar la reducción en la tasa de humedad del suelo y expresar estas relaciones en términos de los efectos de la sequía sobre el comportamiento de las plantas. Las definiciones operacionales se utilizan para analizar la frecuencia, intensidad y duración de un período seco histórico dado. Tales definiciones, sin embargo, requieren datos meteorológicos por hora, día, mes, u otras escalas de tiempo y, posiblemente, los datos de impacto (por ejemplo, el rendimiento del cultivo). Una climatología de la sequía para una región determinada proporciona una mayor comprensión de sus características y la probabilidad de recurrencia en varios niveles de severidad. Este tipo de información es beneficiosa para la formulación de estrategias de mitigación. Tipos de sequía Se han identificado los siguientes tipos de sequía: Sequía metereológica, Sequía agrícola, Sequía hidrológica, y Sequía socioeconómica. ------------------------------------- STOP HERE 230902 10:00 ------------------------------------- La sequía meteorológica se define sobre la base del grado de sequedad, en comparación con una cantidad normal o promedio, y la duración del período seco. Las definiciones de sequía meteorológica deben ser específicas de la región, ya que las condiciones atmosféricas que resultan en deficiencias de precipitación son muy variables. La variedad de definiciones meteorológicas en diferentes países ilustra por qué no es posible aplicar una definición de sequía desarrollado en una parte del mundo a otra. Por ejemplo, se han notificado las siguientes definiciones de sequía: Estados Unidos (1942): Menos de 2.5 mm de lluvia en 48 horas. Gran Bretaña (1936): Quince días consecutivos con precipitación diaria de menos de 0.25 mm. Libia (1964): Cuando la precipitación anual es inferior a 180 mm. Bali (1964): Un período de seis días sin lluvia. Los conjuntos de datos necesarios para evaluar la sequía meteorológica son: (1) precipitación diaria, (2) temperatura, (3) humedad, (4) velocidad del viento, y (5) evaporación. La sequía agrícola relaciona diversas características de la sequía meteorológica a efectos agrícolas. Enfoca la escasez de precipitaciones, las diferencias entre la evapotranspiración real y potencial, el déficit de agua del suelo, y reducción de los niveles de agua subterránea o de los embalses. La demanda de agua de una planta depende de las condiciones climáticas imperantes, las características biológicas de la planta, su etapa de crecimiento, y las propiedades físicas y biológicas del suelo. Una buena definición de sequía agrícola debe tener en cuenta la susceptibilidad de los cultivos durante las diferentes etapas de desarrollo del cultivo. La deficiencia de humedad en la capa superior del suelo puede impedir la germinación, lo cual conduce a bajas poblaciones de plantas por hectárea y una reducción de la productividad. Los conjuntos de datos necesarios para evaluar una sequía agrícola son los siguientes: (1) textura del suelo, (2) fertilidad del suelo, (3) humedad del suelo, (4) el tipo y área de cultivo, y (5) las necesidades de agua del cultivo, (6) las plagas, y (7) el clima. ------------------------------------- STOP HERE 230904 08:30 ------------------------------------- Una sequía hidrológica se refiere a un persistente caudal bajo y/o volumen de agua en arroyos y embalses, los cuales pueden durar meses o años. La sequía hidrológica es un fenómeno natural, pero puede ser exacerbada por actividades humanas. Las sequías hidrológicas están por lo general relacionadas con las sequías meteorológicas, y en consecuencia su intervalo de recurrencia es variable. Los cambios en el uso del suelo y la degradación del suelo pueden afectar la magnitud y frecuencia de sequías hidrológicas. Los conjuntos de datos necesarios para evaluar una sequía hidrológica son: (1) cobertura de área y volumen del agua superficial, (2) escorrentía superficial, (3) mediciones de caudales, (4) infiltración, (5) fluctuaciones del nivel freático, y (6) propiedades del acuífero. La sequía socioeconómica asocia la oferta y la demanda de algún bien económico con elementos de meteorología, hidrología y sequía agrícola. Se diferencia de los otros tipos de sequía en que su aparición depende de procesos de oferta y demanda. El suministro de varios bienes económicos, como el agua, forraje, cereales, pescado, y energía hidroeléctrica, depende del clima. Debido a la variabilidad natural del clima, el suministro de agua es abundante en algunos años, pero insuficiente para satisfacer las necesidades humanas y ambientales en otros años. La sequía socioeconómica se produce cuando la demanda de un bien económico excede a la oferta como resultado de un déficit de suministro de agua relacionado con el clima. La sequía puede dar como resultado una disminución considerable de la producción de energía hidroeléctrica porque las centrales eran dependientes, para la generación de energía, del caudal en lugar del volumen almacenado. La reducción de la producción de energía hidroeléctrica puede llevar al gobierno a convertir a alternativas más caras de petróleo, y comprometerse a medidas de conservación de energía para satisfacer sus necesidades de energía. La demanda de bienes económicos está aumentando como consecuencia del crecimiento demográfico y el desarrollo económico. La alimentación también puede aumentar debido a la mejora de la eficiencia de producción, la tecnología, o la construcción de embalses. Cuando la oferta y la demanda aumentan, el factor crítico es la tasa relativa de cambio. La sequía socioeconómica se promueve cuando la demanda de agua para actividades económicas es muy superior a la oferta. Los conjuntos de datos necesarios para evaluar la sequía socioeconómica son: (1) población humana y animal, (2) tasa de crecimiento, (3) necesidades de agua y forraje, (4) severidad de la pérdida de cosechas, y (5) tipo de industria y requerimientos de agua. ------------------------------------- STOP HERE 230904 10:30 ------------------------------------- Relaciones de Intensidad-Duración-Frecuencia Las relaciones entre la intensidad, duración y frecuencia de sequías pueden ser analizadas por el modelo conceptual descrito en la Tabla 6-6 [27]. El enfoque conceptual es aplicable a las sequías meteorológicas que duran por lo menos un año, en las regiones de latitudes subtropicales y medias en las cuales el clima predominante pueda ser caracterizado principalmente por la precipitación media The climate types, from superarid to superhumid, are defined in terms of mean annual precipitation Pma (mm) as shown in Table 6-6, Line 1: Los tipos de clima, desde superárido a superhúmedo, se definen en términos de la precipitación media anual Pma (mm) como se muestra en la Tabla 6-6, Línea 1: • Super árido:  Pma ≤ 100 • Hiperárido:  100 < Pma ≤ 200 • Árido:  200 < Pma ≤ 400 • Semiárido:  400 < Pma ≤ 800 • Subhúmedo:  800 < Pma ≤ 1600 • Húmedo:  1600 < Pma ≤ 3200 • Hiperhúmedo:  3200 < Pma ≤ 6400 • Superhúmedo:  Pma > 6400 ------------------------------------- STOP HERE 230915 10:00 ------------------------------------- La precipitación terrestre global (media) anual es Pagt = 800 mm [27]. En los extremos del espectro climático, la precipitación media anual es inferior a 100 mm (superárido), o mayor que 6400 mm (superhúmedo). El ejemplo superárido es el desierto de Atacama, en el norte de Chile, con una precipitación media anual de Pma = 0.5 mm, lo cual no es medible. El ejemplo superhúmedo es Cherrapunji, en Meghalaya, al este de la India, con una precipitación media anual de Pma = 11,777 mm, considerado por muchas personas como el lugar más húmedo de la Tierra. Sin embargo, Mawsynran, cerca de Cherrapunji, ahora cuenta con Pma = 11,873 mm, efectivamente superando a Cherrapunji de la distinción. Los tipos de climas también pueden definirse como la relación entre la precipitación media anual Pma y la precipitación terrestre global (media) anual Pagt (Línea 2). La relación de Pma/Pagt = 1 representa la media del espectro climático. El modelo conceptual también se define en términos de la evaporación potencial anual (evapotranspiración) Eap (línea 3) y de la relación de evaporación potencial anual a la precipitación media anual Eap/Pma (línea 4). La relación Eap/Pma = 2 describe el centro del espectro climático. Para complementar la descripción, también se indica la longitud de la temporada de lluvias Lrs (línea 5).  Tabla 6-6  Modelo conceptual de intensidad-duración-frecuencia de sequías [27]. Descripción Superárido ← Hiperárido → Árido → Semiárido → Subhúmedo → Húmedo → Hiperhúmedo → Superhúmedo → 1 Precipitación media anual Pma (mm) 100 200 400 800 1600 3200 6400 2 Pma / Pagt 0.125 0.25 0.5 1 2 4 8 3 Evaporación potencial anual Eap (mm) 3000 2400 2000 1600 1200 1200 1200 4 Eap / Pma 30 12 5 2 0.75 0.375 0.1875 5 Longitud de la estación de lluvias Lrs (meses) 1 2 3 4 6 9 12 6 • Intensidad de sequía Moderada 0.25 0.5 1 1.5 1 0.5 0.25 7 Severa 0.5 1 2 3 2 1 0.5 8 Extrema 0.75 1.5 3 4.5 3 1.5 0.75 9 • Duración de sequía (años) 1 2 4 6 4 2 1 10 •  Frecuencia de sequía (años) -1 2 3 6 12 25 50 +100 ------------------------------------- STOP HERE 230915 10:30 ------------------------------------- Para cualquier año para el que P es la precipitación anual, la intensidad de la sequía I se define como la razón del déficit (Pma - P) a la media (Pma). Para cualquier año, una intensidad I = 0.25 se clasifica como moderada; I = 0.5 severa, y I = 0.75 extrema. Para duraciones de sequía que duran dos años o más, la intensidad es la suma de las intensidades anuales individuales (Líneas 6-8, Tabla 6-6). Por lo tanto, cuanto más tiempo dure la sequía, mayor es la intensidad de la sequía. Las intensidades extremas están generalmente asociadas con sequías de larga duración. 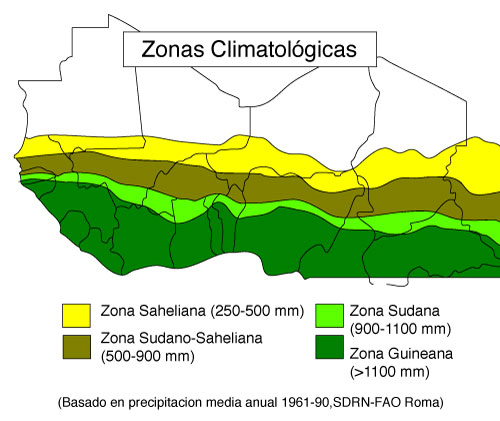La experiencia ha demostrado que las sequías más largas generalmente se producen alrededor del centro del espectro climático (800 mm de precipitación media anual). La duración de sequía varía entre 1 año (o menos) en los extremos del espectro climático y alrededor de 6 años en el centro (Línea 9) [26]. Las sequías que duran más de 6 años son poco comunes; son más probables que sean impulsadas por las presiones antropogénicas, por ejemplo, deforestación o pastoreo excesivo [25]. Un ejemplo clásico de una sequía causada por antropogenia es la del Sahel, en África del Norte (Fig. 6-9), en donde, en los últimos 40 años, las sequías han tenido una tendencia a persistir durante períodos mucho más largos de lo normal. 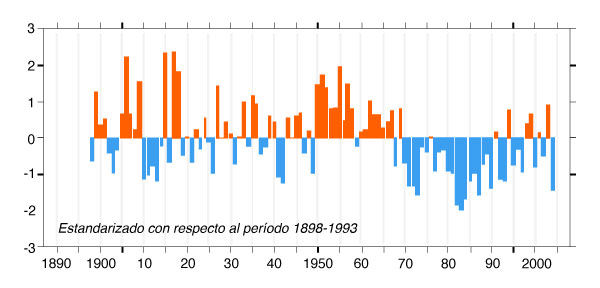La Figura 6-10 muestra valores de precipitación anual normalizada estacional (Junio-Octubre) en el Sahel para el período 1898-2004. La precipitación anual normalizada tiene una media cero y una desviación estándar unitaria. Téngase en cuenta que a través de la década de 1980, la sequía en el Sahel persistió durante más de 10 años. Figura 6-9   Precipitación anual media en el Sahel, África del Norte. Figura 6-10  Precipitación anual normalizada en el Sahel para el período de 1898-2004. En general, los períodos secos (eventos de sequía) son seguidos por períodos húmedos correspondientes. Por lo tanto, el intervalo de recurrencia de las sequías (es decir, el recíproco de la frecuencia) es siempre mayor que la duración. Los intervalos de recurrencia de sequía aumentan de 2 años en el lado extremo seco del espectro climático (superárido,) a (más de) 100 años en el lado extremo húmedo (superhúmedo) (línea 10, Tabla 6-6). PREGUNTAS [Problemas]   [Bibliografía]   •   [Arriba]   [Conceptos de Estadística]   [Análisis de Frecuencia]   [Frecuencia de Flujo Bajo]   [Sequías]   En el análisis estadístico: ¿Cuáles son las medidas de tendencia central? Explicar. ¿Qué es la asimetría? Una distribución con una larga cola en el lado derecho tiene asimetría positiva o negativa? ¿Cuáles son los parámetros de la distribución Gamma? ¿Cómo están relacionadas las distribuciones Gamma y Pearson Tipo III? ¿Cuál es el parámetro que distingue a las tres distribuciones de valores extremos? ¿Cuál es el valor límite de la media de la variable aleatoria de Gumbel? ¿Cuál es la diferencia entre la serie anual de excedencia y la serie de máximos anuales? ¿Qué es riesgo en el contexto de análisis de frecuencia? ¿Cómo se construye un papel de probabilidades de valores extremos? ¿Qué tipo de papel de probabilidades se utiliza en el método de Log Pearson Tipo III? ¿Cuál es la diferencia entre las fórmulas de posición de Weibull, Blom y la de Gringorten? ¿Cómo se toma en cuenta la variabilidad asimétrica en el método de Log Pearson III? ¿Cuándo son los valores altos atípicos considerados parte de los datos históricos? ¿Cuándo es necesario realizar un cálculo histórico ponderado ? ¿Por qué son las distribuciones de dos parámetros, tales como la distribución de Gumbel, apropiadas para su uso en conexión con longitudes de registro cortos? Comparar avenidas y sequías desde el punto de vista del análisis de frecuencia. ¿Cuál es la precipitación media anual en el centro del espectro climático? ¿Cuál es la evaporación potencial media anual en el centro del espectro climático? ¿Por qué las sequías en el Sahel son probables que persistan mucho más tiempo de lo normal? ------------------------------------- STOP HERE 230915 13:00 ------------------------------------- PROBLEMAS [Bibliografía]   •   [Arriba]   [Conceptos de Estadística]   [Análisis de Frecuencia]   [Frecuencia de Flujo Bajo]   [Sequías]   [Preguntas]   Desarrollar una hoja de cálculo para calcular la media, la desviación estándar y el coeficiente de asimetría de una serie de caudales máximos anuales. Probar el cálculo utilizando los datos del Ejemplo 6-1 en el texto. Se han encontrado los flujos máximos anuales de un determinado flujo distribuido normalmente con una media de 22,500 pies3/s y desviación estándar de 7500 pies3/s. Calcular la probabilidad de que ocurra un flujo mayor de 39,000 pies3/s. Las avenidas de período de retorno de 10 años y 25 años de una determinada corriente son 73 y 84 m3/s, respectivamente. Suponiendo una distribución normal, calcular las avenidas de 50 y 100 años. Los flujos bajos de cierta corriente siguen una distribución normal. Los flujos esperados que exceden el 95% y el 90% de las veces son 15 y 21 m3/s, respectivamente. ¿Qué flujo se espera que exceda 80% del tiempo? Una ataguía temporal para un período de 5 años de construcción de una presa está diseñada para pasar la avenida de 25 años. ¿Cuál es el riesgo de que la ataguía pueda fallar antes de que finalice el período de construcción? ¿Qué período de retorno de diseño es necesaria para reducir el riesgo a menos del 10%? Use la fórmula de Weibull (Ec. 6-26) para calcular las posiciones de trazado para la siguiente serie de máximos anuales, en pies cúbicos por segundo: 1305, 3250, 4735, 5210, 4210, 2120, 2830, 3585, 7205, 1930, 2520, 3250, 5105, 4830, 2020, 2530, 3825, 3500, 2970, 1215. Utilice la fórmula de Gringorten para calcular las posiciones graficadas para la siguiente serie de máximos anuales, en metros cúbicos por segundo: 160, 350, 275, 482, 530, 390, 283, 195, 408, 307, 625, 513. Modifique la hoja de cálculo del Problema 6-1 para calcular la media, la desviación estándar y el coeficiente de sesgo de los logaritmos de una serie de flujos máximos anuales. Pruebe el cálculo utilizando los resultados del Ejemplo 6-4 en el texto. ------------------------------------- STOP HERE 230920 16:00 ------------------------------------- Ajuste una curva de Log Pearson III en los datos del Problema 6-6. Represente gráficamente la distribución calculada en el papel logarítmico de probabilidad, junto con las posiciones gráficas de Weibull calculadas en el Problema 6-6. Ajuste una curva de Gumbel a los datos del Problema 6-6. Represente gráficamente la distribución calculada en papel de Gumbel, junto con las posiciones gráficas de Weibull calculadas en el Problema 6-6. Desarrolle una hoja de cálculo para leer una serie de máximos anuales, ordenar los datos en orden descendente, y calcular las posiciones gráficas correspondientes (por ciento de posibilidades y período de retorno) por las fórmulas de Weibull y Gringorten. Dadas las siguientes estadísticas de caudales máximos anuales para el flujo X: número de años n = 35; media = 3545 pies3/s; desviación estándar = 1870 pies3/s. Calcular la avenida de 100 años por el método de Gumbel. Teniendo en cuenta las siguientes estadísticas de caudales máximos anuales para el río Y: número de años n = 45; caudal medio = 2700 m3/s; desviación estándar 1300 m 3/s; media de los logaritmos = 3,1; desviación estándar de los logaritmos = 0,4; y coeficiente de asimetría de los logaritmos = -0,35. Calcular la avenida de 100 años utilizando las siguientes distribuciones de probabilidades: (a) normal, (b) Gumbel, y (c) Log Pearson III. Una estación cerca de Denver, Colorado, tiene los registros de avenidas de 48 años, con el coeficiente de sesgo de la estación Csy = - 0.18 Calcular un coeficiente de sesgo ponderado. Determinar si el valor Q = 13,800 pies3/s es un alto valor atípico en una serie de avenidas de 45 años con los siguientes datos: media de los logaritmos = 3.572; desviación estándar de los logaritmos = 0,215. Using the Lettenmaier and Burges modification to the Gumbel method, fit a Gumbel curve to the data of Example 6-6 in the text. Plot the calculated distribution on Gumbel paper, along with plotting positions calculated by the Gringorten formula. Usando la modificación Lettenmaier y Burges al método de Gumbel, ajuste una curva Gumbel a los datos del Ejemplo 6-6 del texto. Represente gráficamente la distribución calculada en papel de Gumbel, junto con las posiciones gráficas calculadas por la fórmula de Gringorten. ------------------------------------- STOP HERE 230920 18:00 ------------------------------------- BIBLIOGRAFÍA •   [Arriba]   [Conceptos de Estadística]   [Análisis de Frecuencia]   [Frecuencia de Flujo Bajo]   [Sequías]   [Preguntas]   [Problemas]   Benson, M. A. (1962). "Plotting Positions and Economics of Engineering Planning," Journal of the Hydraulics Division, ASCE, Vol. 88, Noviembre, pp. 57-71. Benson, M. A. (1968). "Uniform Flood Frequency Estimating Methods for Federal Agencies," Water Resources Research, Vol. 4, pp. 891-908. Blom, G. (1958). Statistical Estimates and Transformed Beta Variables. New York: John Wiley. Casella, G., and R. L. Berger. (1990). Statistical Inference, Wadsworth & Brooks/Cole, Pacific Grove, California. Chow, V. T. (1951). "A General Formula for Hydrologic Frequency Analysis," Transactions, American Geophysical Union, Vol. 32, pp. 231-237. Chow, V. T. (1964). Handbook of Applied Hydrology. Nueva York: McGraw-Hill. Cunnane, C. (1978). "Unbiased Plotting Positions-A Review," Journal of Hydrology, Vol. 37, pp. 205-222. Fisher, R. A., and L. H. C. Tippett. (1928). "Limiting Forms of a Frequency Distribution of the Smallest and Largest Member of a Sample," Proceedings, Cambridge Philosophical Society, Vol. 24, pp.180-190. Foster, H. A. (1924). "Theoretical Frequency Curves and their Application to Engineering Problems," Transactions, ASCE, Vol. 87, pp. 142-173. Frechet, M. (1927). "Sur la loi de Probabilite de l'ecart Maximum," (On the Probability Law of Maximum Error), Annals of the Polish Mathematical Society, (Cracow), Vol. 6, pp. 93-116. Fuller, W. E. (1914). "Flood Flows," Transactions, ASCE, Vol. 77, pp. 564-617. Gringorten, 1.1. (1963). "A Plotting Rule for Extreme Probability Paper," Journal of Geophysical Research, Vol. 68, No.3, February, pp. 813-814. Gumbel, E. J. (1941). "Probability Interpretation of the Observed Return Periods of Floods," Transactions, American Geophysical Union, Vol. 21, pp. 836-850. Gumbel, E. J. (1942). "Statistical Control Curves for Flood Discharges," Transactions, American Geophysical Union, Vol. 23, pp. 489-500. K Gumbel , E. J. (1943). "On the Plotting of Flood Discharges," Transactions, American Geophysical Union, Vol. 24, pp. 699-719. Gumbel, E. J. (1958). Statistics of Extremes. Irvington, N.Y.: Columbia University Press. Hazen, A. (1914). Discussion on "Flood Flows," by W. E. Fuller, Transactions, ASCE, Vol. 77, p. 628. Havens, A. V. (1954). "Drought and Agriculture," Weatherwise, Vol. 7, pp. 51-55. Horton, R. E. (1913). "Frequency of Recurrence of Hudson River Floods," U.S. Weather Bureau Bulletin Z, pp. 109-112. Jenkinson, A. F. (1955). "The Frequency Distributions of the Annual Maximum (or Minimum) Values of Meteorological Elements," Quarterly Journal of the Royal Meteorological Society, Vol. 87, p. 158. Kite, G. W. (1977). Frequency and Risk Analyses in Hydrology. Fort Collins, Colorado: Water Resources Publications. Lettenmaier, D. P., y S. J. Burges. (1982). "Gumbel's Extreme Value Distribution: A New Look," Journal of the Hydraulics Division, ASCE, Vol. 108, No. HY4, Abril, pp. 503-514. Natural Environment Research Council. (1975). Flood Studies Report. Vol. 1 (of 5 volumes), London, England. Pearson, K. (1930). "Tables for Statisticians and Biometricians," Part I, 3d. Ed. , The Biometric Laboratory, University College. London: Cambridge University Press. Ponce, V. M., A. K. Lohani, and P. T. Huston. (1997). "Surface albedo and water resources: Hydroclimatological impact of human activities." Journal of Hydrologic Engineering, ASCE, Vol. 2, No. 4, October, 197-203. Ponce, V. M., R. P. Pandey, y S. Ercan. (1999). "A conceptual model of drought characterization across the climatic spectrum." Revista de Estudos Ambientais, Vol. 1, No. 3, septiembre-diciembre, 68-76. Ponce, V. M., R. P. Pandey, y S. Ercan. (2000). "Characterization of drought across climatic spectrum." Journal of Hydrologic Engineering, ASCE, Vol. 5, No. 2, Abril, 222-224. Riggs, H. C. (1972). "Low-Flow Investigations," Techniques of Water Resources Investigations of the United States Geological Survey, Book 4, Chapter B1. Spiegel, M. Mathematical Handbook of Formulas and Tables. Schaum's Outline Series in Mathematics. New York: McGraw-Hill. Troxell, H. C. (1937). "Water Resources of Southern California with Special Reference to the Drought of 1944-51," U.S. Geological Survey Water Supply Paper No. 1366. U.S. Interagency Advisory Committee on Water Data, Hydrology Subcommittee. (1983). "Guidelines for Determining Flood Flow Frequency," Bulletin No. 17B, issued 1981, revised 1983, Reston, Virginia. Lecturas sugeridas Gumbel, E. J. (1958). Statistics of Extremes. Irvington, N.Y.: Columbia University Press. Natural Environment Research Council. (1975). Flood Studies Report, in 5 volumes, London, England. Riggs, H. C. (1972). "Low-Flow Investigations," Techniques of Water Resources Investigations of the United States Geological Survey, Book 4, Chapter B1. U.S. Interagency Advisory Committee on Water Data, Hydrology Subcommittee. (1983). "Guidelines for Determining Flood Flow Frequency," Bulletin No. 17B, issued 1981, revised 1983, Reston, Virginia. http://engineeringhydrology.sdsu.edu 230920