|
|
|
CAPÍTULO 10: FLUJO NO PERMANENTE GRADUALMENTE VARIADO |
10.1 ECUACIONES DE GOBIERNO
|
|
Three conservation principles are applicable in open-channel flow:
Se aplican tres prncipios de conservación en el flujo en canales:
Conservation of mass, which could be either: (a) steady, or (b) unsteady,
Conservación de masa, la cual puede ser: (a) permanente, o (b) no permanente,
Conservation of energy, which is steady (recall that energy is equal to the integral of all forces, excluding inertia,
in space, Eq. 2-15), andLa conservación de la energía, la cual es permanente (debido a que la energía es igual a la integral de todas las fuerzas en el espacio, excluyendo la inercia Ec. 2-15), y
Conservation of momentum, which is unsteady (recall that momentum is equal to the integral of the inertia force
in time, Eq. 2-27).La conservación del momento, que es no permanente (debido a que el momento es igual a la integral de la fuerza de inercia
en el tiempo, Ec. 2-27).
Steady gradually varied flow combines the statements of steady conservation of mass and conservation of energy (Chapter 7). Unsteady gradually varied flow combines the statements of unsteady conservation of mass and conservation of momentum (Table 10-1). Thus, unsteady gradually varied flow differs from steady gradually varied flow in its description of the temporal variation of the flow variables (discharge, stage, flow depth, mean velocity, and so on).
Flujo permanente gradualmente variado combina las declaraciones de la conservación permanente de la masa y de la energía (Capítulo 7). El flujo no permanente gradualmente variado combina las declaraciones de la conservación no permanente de la masa y del momento (Tabla 10-1). Por lo tanto, el flujo no permanente gradualmente variado difiere del flujo permanente gradualmente variado en su descripción de la variación temporal de las variables de flujo (descarga, etapa, profundidad de flujo, velocidad media, etc.).
In practice, steady gradually varied flow is simply referred to as "gradually varied flow" (GVF), while unsteady gradually varied flow is commonly referred to as "unsteady flow" (UF).
En la práctica, el flujo permanente gradualmente variado se refiere simplemente como "flujo gradualmente variado" (FGV), mientras el flujo no permanente gradualmente variado se conoce comúnmente como "flujo no permanente" (UF).
| Table 10-1
Conservation laws and types of gradually varied flow. Tabla 10-1 Leyes de conservación y tipos de flujo gradualmente variado. | |||
| Model/Modelo | Primera ecuación: Conservation of mass, either /Conservación de la masa, ya sea→ | Steady mass / Masa permanente | Masa no permanente |
| Segunda ecuación: Conservación de → | Energía | Momento | |
| Flujo | Tipo (nombre) → | Steady GVF / Permanente GVF | Unsteady GVF / No permanente GVF |
| Comúnmente conocido como → | Gradually varied flow / Flujo gradualmente variado | Unsteady flow / Flujo no permanente | |
| Treated in / Visto en → | Capítulo 7 | Capítulo 10 (capítulo actual) | |
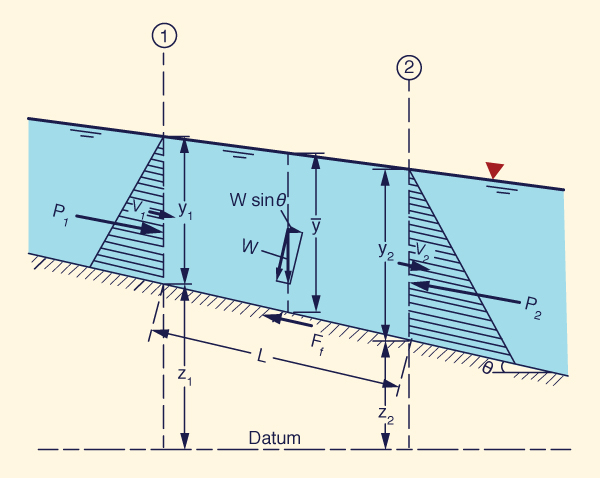
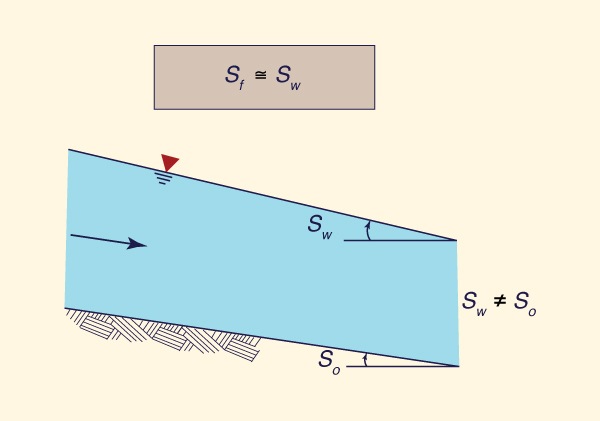
Figure 10-1 depicts the forces acting on a control volume. One body force and two surface forces are shown. The body force is the component of the gravitational force resolved along the direction of motion (W sin θ). The surface forces are: (1) the force due to the pressure gradient (due to the difference in flow depths), ΔP = P2 - P1, and (2) the force developed along the bottom boundary due to friction (Ff ). When these three forces are in equilibrium along the direction of motion, the flow is steady from the force standpoint. When the three forces are NOT in equilibrium along the direction of motion, the flow is unsteady and a fourth force arises (the inertia force) to produce a balance.
La Figura 10-1 muestra las fuerzas que actúan sobre un volumen de control. Se muestra una fuerza de cuerpo y dos fuerzas de superficie. La fuerza de cuerpo es el componente de la fuerza gravitacional que actúa a lo largo de la dirección del movimiento (W sin θ). Las fuerzas de superficie son: (1) la fuerza debida al gradiente de presión (que se presenta por la diferencia de profundidades de flujo), ΔP = P2 - P1, y (2) la fuerza desarrollada a lo largo del lecho del canal debido a la fricción (Ff ). Cuando estas tres fuerzas están en equilibrio a lo largo de la dirección del movimiento, el flujo es constante desde el punto de vista de la fuerza. Cuando las tres fuerzas NO se encuentran en equilibrio a lo largo de la dirección del movimiento, el flujo es inestable y surge una cuarta fuerza (la fuerza de inercia) para producir equilibrio.
|
Ecuaciones de gobierno
The derivation of the governing equations of unsteady flow (Fig. 10-2) (unsteady gradually varied flow) considers the statements of mass and momentum conservation in a control volume (Fig. 10-3).
La derivación de las ecuaciones de gobierno del flujo no permanente (flujo no permanente gradualmente variado) (Fig. 10-2) considera las declaraciones de la conservación de masa y momento en un volumen de control (Fig. 10-3).
|
|
The statement of conservation of mass is:
El estado de conservación de la masa es:
|
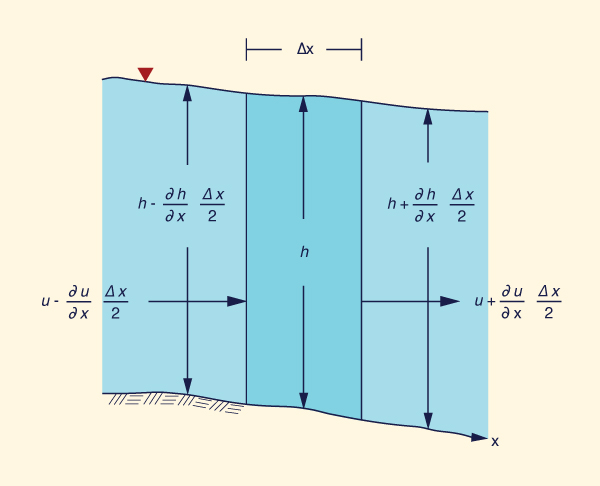
For a unit-width channel (Liggett, 1975):
Para un canal de ancho de una unidad (Liggett, 1975):
|
∂u Δx ∂h Δx ∂u Δx ∂h Δx ∂h (u - ____ ____ ) (h - ____ ____ ) - (u + ____ ____ ) (h + ____ ____ ) = ____ Δx ∂x 2 ∂x 2 ∂x 2 ∂x 2 ∂t |
| (10-1) |
Simplifying, and neglecting second-order terms as Δx → 0:
Simplificando, y despreciando los términos de segundo orden como Δx → 0:
|
∂h ∂h ∂u ____ + u ____ + h ____ = 0 ∂t ∂x ∂x | (10-2) |
|
∂h ∂ ____ + ____ (uh) = 0 ∂t ∂x | (10-3) |
Equation 10-3 is the unsteady conservation of mass equation, commonly referred to as the equation of continuity. However, its complete name is: the differential equation of water continuity.
La ecuación 10-3 es la ecuación de la conservación no permanente de la masa, comúnmente conocida como la ecuación de continuidad. Sin embargo, su nombre completo es: la ecuación diferencial de la continuidad del agua.
For steady flow: ∂h/∂t = 0, and Eq. 10-3 reduces to: q = uh = constant. In general, for a channel of flow area A, the steady water continuity equation is: Q = uA = constant.
Para el flujo permanente: ∂h/∂t = 0, y la Ec. 10-3 se reduce a: q = uh = constante. En general, para un canal de área de flujo A, la ecuación de continuidad permanente de agua es: Q = uA = constante.
The statement of conservation of momentum is:
El estado de conservación del momento es:
|
The momentum, per unit of channel width, is: ρ u (uh). Therefore, the net rate of momentum entering the control volume FΔ (force per unit of width) is:
El momento, por unidad de ancho del canal, es: ρ u (uh). Por lo tanto, la tasa neta del momento entrando al volumen de control FΔ (fuerza por unidad de ancho) es:
|
∂ Δx ∂ Δx FΔ = ρ { u (u h) - ____ [ u (u h) ] ____ } - ρ { u (u h) + ____ [ u (u h) ] ____ } ∂x 2 ∂x 2 |
| (10-4) |
The forces acting on the control volume, resolved along the direction of motion, are: (1) gravitational force, (2) pressure-gradient force, and (3) frictional force (Fig. 10-1).
Las fuerzas que actúan sobre el volumen de control, a lo largo de la dirección del movimiento, son: (1) la fuerza de gravedad, (2) la fuerza de presión-gradiente, y (3) la fuerza de fricción (figura 10-1.).
The gravitational force, per unit of width, is:
La fuerza gravitacional, por unidad de ancho es:
|
Fg = ρ g h Δx sin θ ≅ ρ g h Δx tan θ = ρ g h Δx So | (10-5) |
The pressure-gradient force, per unit of width, developed along the sides of the control volume, is:
La fuerza de presión-gradiente, por unidad de ancho, desarrollado a lo largo de los lados del volumen de control, es:
|
h h 1 Fp = ∫ p dz = ρ g ∫ (h - z ) dz = = ____ ρ g h 2 0 0 2 | (10-6) |
The frictional force, per unit of width, developed along the channel bottom, resembles the gravitational force, but it is opposite in sign:
La fuerza de fricción, por unidad de ancho desarrollado a lo largo del lecho del canal, se asemeja a la fuerza de la gravedad, pero es de signo opuesto:
|
Ff = - ρ g h Δx Sf | (10-7) |
in which Sf = friction slope. [As an exception, for channels of adverse bottom slope, for which So < 0, the gravitational and frictional forces are of the same sign].
en la cual Sf = pendiente de fricción. [Como una excepción, para canales de pendiente de fondo adversa, para los cuales So < 0, las fuerzas de gravedad y de fricción son del mismo signo].
The size of the control volume, per unit of width, is:
El tamaño del volumen de control, por unidad de ancho, es:
|
∂ Fm = ____ (ρ u h) Δx ∂t | (10-8) |
The conservation of momentum is:
La conservación del momento es:
|
FΔ + Fg + Fp + Ff = Fm | (10-9) |
Replacing Eqs. 10-4 to 10-8 into Eq. 10-9:
Sustituyendo las Ecs. 10-4 a la 10-8 dentro de la Ec. 10-9:
|
∂ Δx ∂ Δx ρ { (u 2 h ) - ____ (u 2 h ) ____ } - ρ { (u 2 h ) + ____ (u 2 h ) ____ } + ρ g h Δx So ∂x 2 ∂x 2 |
|
1 ∂h 2 Δx ∂h 2 Δx + ____ ρ g [ (h 2 - _____ ____ ) - (h 2 + _____ ____ ) ] + ρ g h Δx Sf 2 ∂x 2 ∂x 2 |
|
∂ = ____ (ρ u h) Δx ∂t | (10-10) |
Simplifying Eq. 10-10:
Simplificando la Ec. 10-10:
|
∂ ∂ g ∂h 2 ____ (u h ) + ____ (u 2 h ) + ____ ______ = g h (So - Sf ) ∂t ∂x 2 ∂x | (10-11) |
Equation 10-11 is in conservation form. For certain applications, it must remain in this form. However, it is often expressed in reduced form, by operating on the derivatives:
La ecuación 10-11 está en forma de conservación. Para ciertas aplicaciones, debe permanecer en esta forma. Sin embargo, a menudo se expresa en forma reducida, al resolver para las derivadas:
|
∂u ∂h ∂ ∂u ∂h h ____ + u ____ + u ____ (u h ) + (u h ) ____ + g h ____ = g h (So - Sf ) ∂t ∂t ∂x ∂x ∂x |
| (10-12) |
The second and third terms of Eq. 10-12 have implicit in them the continuity equation (Eq. 10-3). Thus, Eq. 10-12 reduces to:
El segundo y tercer términos de la Ec. 10-12 tienen implícita la ecuación de continuidad (Ec. 10-3). Por lo tanto, la Ec. 10-12 se reduce a:
|
∂u ∂u ∂h ____ + u ____ + g ____ + g (Sf - So ) = 0 ∂t ∂x ∂x | (10-13) |
By dividing by g, Eq. 10-13 is expressed in slope units:
Dividiendo por g, la Ec. 10-13 se expresa en unidades de pendiente:
|
1 ∂u u ∂u ∂h ____ _____ + ____ _____ + _____ + (Sf - So ) = 0 g ∂t g ∂x ∂x | (10-14) |
Equation 10-14 is referred to as the equation of motion. It is expressed in terms of slopes as follows:
La Ecuación 10-14 se conoce como la ecuación de movimiento.
Se expresa en términos de pendientes como sigue:
|
Sa + Sc + Sp + Sf - So = 0 | (10-15) |
in which Sa = local acceleration slope, Sc = convective acceleration slope, Sp = pressure-gradient slope, Sf = friction slope, and So = bottom slope.
en la cual Sa = pendiente de aceleración local,
Sc = pendiente de aceleración convectiva,
Wave types / Tipos de ondas
Equation 10-15 indicates that the momentum balance is essentially a balance of slopes. In the general case, when all forces are present, all slopes are acting and the solution is the most general. In certain cases, however, one or more slopes may be reduced to zero, or assumed to be negligible (compared to the remaining slopes). This simplification gives rise to several types of waves, described in Table 10-2.
La Ecuación 10-15 indica que el balance de momento es esencialmente un equilibrio de pendientes. En el caso general, cuando todas las fuerzas están presentes, todas las pendientes están actuando y la solución es la más general. Sin embargo, en ciertos casos, una o más pendientes pueden reducirse a cero, o se suponen como insignificantes (comparadativamente con las demás pendientes). Esta simplificación da lugar a varios tipos de ondas, que se describen en la Tabla 10-2.
| Table 10-2 Types of waves in unsteady open-channel flow. / Tipos de ondas presentes en flujo no permanente en canales. | ||||||||
| No. | Tipo de onda | Pendientes | Nombre común | Aplicaciones | Sa
| Sc
| Sp
| Sf
| So
| 1
| Kinematic wave / Onda cinemática
|
|
|
| ✓
| ✓
| Kinematic wave / Onda cinemática
| Overland flow / Flujo superficial
|
|
| ✓
| ✓
| ✓
| Diffusion wave / Onda de difusión
| Flood routing / Tránsito de avenidas
| 3
| Dynamic wave / Onda dinámica
| ✓
| ✓
| ✓
|
|
| Gravity | wave / Onda de gravedad small canals canales pequeños 4
| Steady-dynamic wave / Onda dinámica permanente
|
| ✓
| ✓
| ✓
| ✓
| Steady-dynamic wave / Onda dinámica permanente
| Special cases / Casos especiales
| 5
| Mixed | ✓
| ✓
| ✓
| ✓
| ✓
| Dynamic wave / Onda dinámica
| Dam-breach | |
|
Applicability of wave types / Aplicabilidad de tipos de ondas
Kinematic waves [1] apply to overland flow, where the bottom slopes are steep, typically greater than So > 0.01. Ondas cinemáticas [1] corresponden al flujo superficial, donde las pendientes de fondo son pronunciadas, típicamente mayor que So > 0.01. Diffusion waves [2] apply to flood routing in streams and rivers, with intermediate bottom slopes (0.01 > So > 0.0001). Ondas de difusión [2] se aplican para tránsito de avenidas en los arroyos y ríos, con pendientes de fondo intermedias (0.01 > So > 0.0001). Dynamic waves [3] apply to the short waves of laboratory flumes and small canals. Ondas dinámicas [3] se aplican a las ondas cortas de canaletas de laboratorio y pequeños canales. Steady-dynamic waves [4] apply to the few special cases where the neglect of the local acceleration term (Sa) is justified on practical grounds. In general, however, it is more accurate to neglect both Sa and Sc (i.e., a diffusion wave [2]) than just Sa (Ponce, 1990). Ondas dinámicas permanentes [4] se aplican a los pocos casos especiales donde el desprecio del término de aceleración local (Sa) se justifica por motivos prácticos. Sin embargo, es mejor despreciar ambas Sa y Sc (es decir, una onda de difusión [2]) que sólo Sa (Ponce, 1990).
Mixed kinematic-dynamic waves [5]
apply to a sudden wave such as that originating in a dam breach, and may
also apply to channels
of very mild slope
Ondas cinemáticas dinámicas mixtas [5] se aplican a una onda repentina
como la que se origina en una falla de presa, también se pueden aplicar a los
canales de pendiente muy suave |
10.2 LINEAR SOLUTION / SOLUCIÓN LINEAL
|
|
Equations 10-2 and 10-14 are the governing equations of continuity and motion, also referred to as the Saint-Venant equations (Saint-Venant, 1871). They are repeated here for convenience, as Eqs. 10-16 and 10-17, respectively.
Las ecuaciones 10-2 and 10-14 son las ecuaciones de gobierno de continuidad y movimiento, también se conocen como las ecuaciones de Saint-Venant (Saint-Venant, 1871). A continuación se vuelven a mostrar por conveniencia, como las Ecs. 10-16 y 10-17, respectivamente.
|
∂h ∂h ∂u ____ + u ____ + h ____ = 0 ∂t ∂x ∂x | (10-16) |
|
1 ∂u u ∂u ∂h ____ _____ + ____ _____ + _____ + (Sf - So ) = 0 g ∂t g ∂x ∂x | (10-17) |
These equations constitute a set of two nonlinear (actually, quasilinear) partial differential equations, which when appropriately combined, result in a second-order partial differential equation of the hyperbolic type, featuring two solutions. To this date, there is no closed-form analytical solution of the set of Eqs. 10-16 and 10-17. An approximate solution may be obtained by linearizing the equation set and using the tools of linear stability analysis (Ponce and Simons, 1977).
Estas ecuaciones constituyen un conjunto de dos ecuaciones diferenciales parciales no lineales (en realidad, cuasi-lineales), que cuando se combinan adecuadamente resultan en una ecuación diferencial parcial de segundo orden de tipo hiperbólico, la cual ofrece dos soluciones. A la fecha, no hay una solución analítica de forma cerrada del conjunto de Ecs. 10-16 y 10-17. Una solución aproximada se puede obtener linealizando el conjunto de ecuaciones y utilizando las herramientas de análisis de estabilidad lineal (Ponce y Simons, 1977).
The friction slope Sf is directly related to the bottom shear stress τ by the expression (similar to Eq. 6-16):
La pendiente de fricción Sf está directamente relacionada al esfuerzo cortante inferior τ por medio de la expresión (similar a la Ec. 6-16.):
|
τ Sf = _____ γ h | (10-18) |
In the usual manner of stability calculations, Eqs. 10-16 and 10-17 must satisfy the unperturbed flow, for which u = uo , h = ho , and τ = τo . They must also satisfy the perturbed flow, for which u = uo + u' , h = ho + h' , and τ = τo + τ' . The superscript ' represents a small perturbation to the steady uniform flow. Thus, all quadratic terms in the fluctuating components may be neglected due to an order-of-magnitude reasoning.
Como es costumbre en los cálculos de estabilidad, las Ecs. 10-16 y 10-17 deben satisfacer al flujo no perturbado, en el cual u = uo , h = ho , y τ = τo. Además, deben satisfacer el flujo perturbado, en el cual u = uo + u' , h = ho + h' , y τ = τo + τ' . El superíndice ' representa una pequeña perturbación al flujo uniforme permanente. Por lo tanto, todos los términos cuadráticos en los componentes fluctuantes pueden ignorarse, ya que son muy pequeños comparativamente.
Substitution of the perturbed variables in Eqs. 10-16, 10-17, and 10-18, yields, after linearization (Lighthill and Whitham, 1955):
La sustitución, después de linealización, de las variables perturbadas en las Ecs. 10-16, 10-17, y 10-18, resulta en (Lighthill y Whitham, 1955):
|
∂h' ∂h' ∂u' ____ + uo ____ + ho ____ = 0 ∂t ∂x ∂x | (10-19) |
|
1 ∂u' uo ∂u' ∂h' τ' h' ____ _____ + ____ _____ + _____ + So ( _____ - _____ ) = 0 g ∂t g ∂x ∂x τo ho | (10-20) |
in which:
en las cuales:
|
τo So = _____ γ ho | (10-21) |
The boundary shear stress τ can be related to the mean velocity u as follows (Eq. 5-3):
El límite del esfuerzo cortante τ se relaciona con la velocidad media u como sigue (Ec 5-3.):
|
τ = f ρ u 2 | (10-22) |
in which the friction factor f is (Eq. 5-12):
en la cual el factor de fricción f es (Eq. 5-12):
| g f = ______ C 2 | (10-23) |
In view of Eq. 10-22, Eq. 10-20 is converted to:
La Ec. 10-20 se modifica de acuerdo a la Ec. 10-22 como sigue:
|
1 ∂u' uo ∂u' ∂h' u' h' ____ _____ + ____ _____ + _____ + - So ( 2 _____ - _____ ) = 0 g ∂t g ∂x ∂x uo ho | (10-24) |
Small perturbation analysis / Análisis de perturbación pequeña
The solution for a small perturbation in the depth of flow is postulated in the following exponential form (Ponce and Simons, 1977):
La solución para una perturbación pequeña en la profundidad de flujo se muestra de la siguiente forma exponencial (Ponce y Simons, 1977):
|
h' ____ = h* e i (σ* x* - β* t* ) ho | (10-25) |
in which the subscript * indicates dimensionless variables, and i = (-1)1/2. The quantity σ* = dimensionless wavenumber, β* = dimensionless complex propagation factor, and x* and t* are dimensionless space and time coordinates, such that:
en la cual el subíndice * indica las variables adimensionales, y i = (-1)1/2. La cantidad σ* = número adimensional de onda, β* = factor adimensional de propagación compleja y x* y t* son coordenadas adimensionales de tiempo y espacio, por lo tanto:
|
2 π σ* = ( _____ ) Lo L | (10-26) |
|
2 π Lo βR* = ( _____ ) _____ T uo | (10-27) |
|
x x* = _____ Lo | (10-28) |
|
uo t* = t _____ Lo | (10-29) |
and βI* is an amplitude propagation factor. The quantity Lo is the length of channel in which the uniform flow drops a head equal to its depth:
y βI* es un factor de propagación de amplitud. La cantidad Lo es la longitud del canal en la cual el flujo uniforme se disminuye en una carga igual a la profundidad:
|
ho Lo = _____ So | (10-30) |
The depth disturbance is associated with a velocity disturbance of the form:
Las perturbaciones de profundidad y velocidad se asocian con la siguiente relación:
|
u' ____ = u* e i (σ* x* - β* t* ) uo | (10-31) |
The substitution of Eqs. 10-25 and 10-31 into Eqs. 10-19 and 10-24 yields the set:
La sustitución de las Ecs. 10-25 y 10-31 en las Ecs. 10-19 y 10-24 produce el conjunto:
|
σ* u* + (σ* - β* ) d* = 0 | (10-32) |
|
[ 2 + i Fo2 (σ* - β* ) ] u* + (i σ* - 1 ) d* = 0 | (10-33) |
in which
en el cual
|
uo 2 Fo2 = ______ g ho | (10-34) |
Equations 10-32 and 10-33 constitute a homogeneous system of linear equations in the unknowns u* and h*. For the solution to be nontrivial, the determinant of the coefficient matrix must vanish. Therefore, the following relation holds:
Las Ecs. 10-32 y 10-33 constituyen un sistema homogéneo de ecuaciones lineales u* y h* como desconocidas. Para que la solución sea no trivial, el determinante de la matriz de coeficientes debe desaparecer. Por lo tanto, la siguiente relación se mantiene:
|
i β* 2 Fo2 - i σ* 2 (1 - Fo2 ) + 3 σ* - 2 β* - 2 i σ* β* Fo2 = 0 | (10-35) |
Equation 10-35 is the characteristic equation governing the propagation of small amplitude water waves. Through algebraic manipulation, Eq. 10-35 reduces to:
La Ec. 10-35 es la ecuación característica que rige la propagación de las ondas de agua de amplitud pequeña. A través de una manipulación algebraica, la Ec. 10-35 se reduce a:
|
Fo2 β* 2 - 2 (σ* Fo2 - i ) β* - [ σ* 2 (1 - Fo2 ) + 3 σ* i ] = 0 | (10-36) |
The solution of Eq. 10-36 is (Ponce and Simons, 1977):
La solución de la Ec. 10-36 es (Ponce y Simons, 1977):
|
1 β* = σ* ( 1 - i ζ ) + σ* [ ( ______ - ζ 2 ) + i ζ ] 1/2 Fo2 | (10-37) |
in which
en la cual
|
1 ζ = _________ σ* Fo2 | (10-38) |
The equations for dimensionless celerity and attenuation for the primary and secondary waves are:
Las ecuaciones para la celeridad adimensional y la atenuación de las ondas primarias y secundarias son:
|
C + A c1* = 1 + ( _________ )1/2 2 | (10-39) |
|
B - E δ1 = - 2π _____________ | 1 + D | | (10-40) |
|
C + A c2* = 1 - ( _________ )1/2 2 | (10-41) |
|
B + E δ2 = - 2π _____________ | 1 - D | | (10-42) |
in which
en las cuales:
|
1 A = ______ - ζ 2 Fo2 | (10-43) |
|
B = ζ | (10-44) |
|
1 C = [ ( ______ - ζ 2 ) 2 + ζ 2 ] 1/2 Fo2 | (10-45) |
|
C + A D = ( _________ )1/2 2 | (10-46) |
|
C - A E = ( _________ )1/2 2 | (10-47) |
The dimensionless relative wave celerity is:
La celeridad relativa adimensional de la onda es:
|
C + A cr* = ( _________ )1/2 = D 2 | (10-48) |
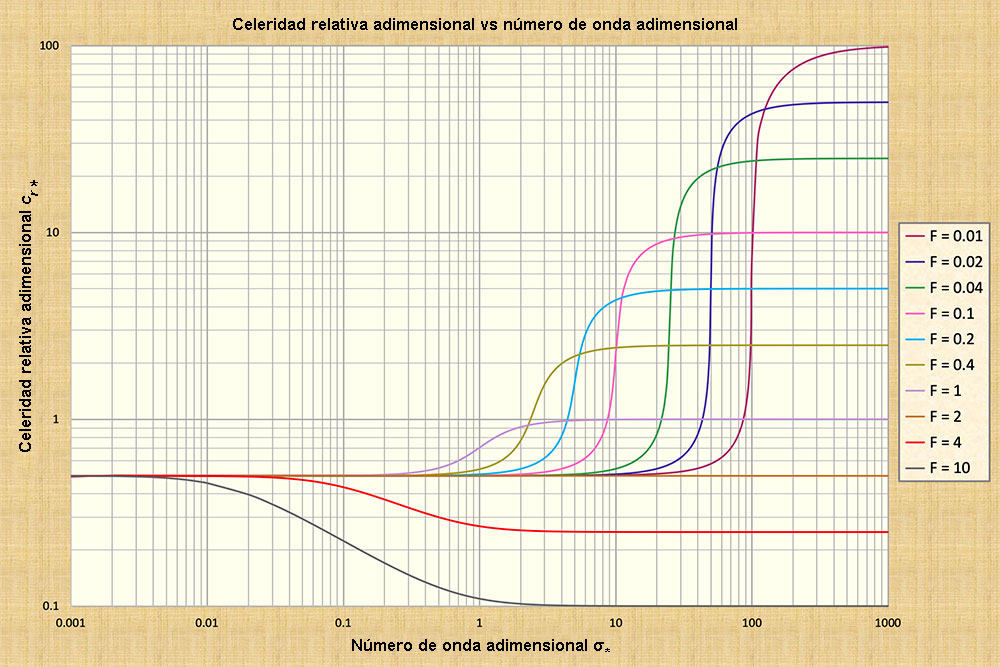
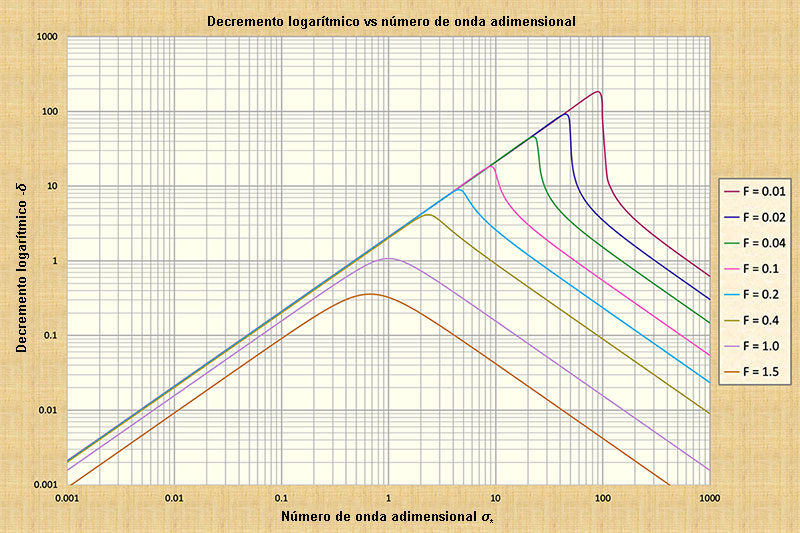
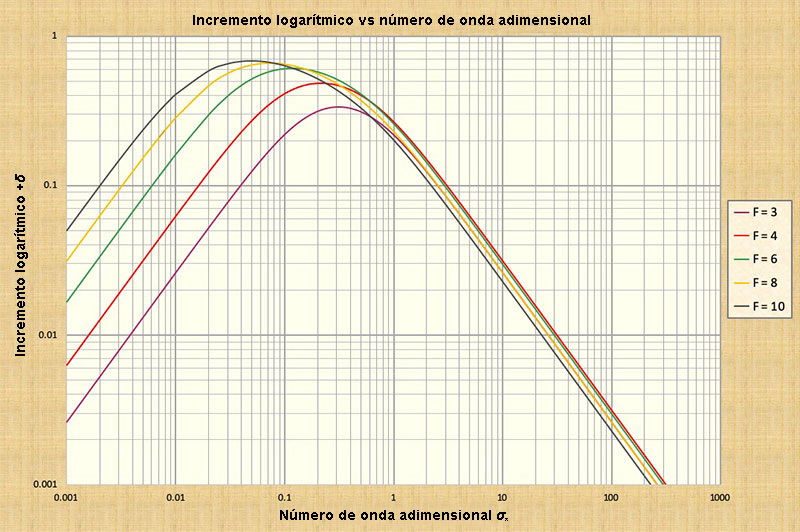
Figure 10-4 shows a plot of the dimensionless relative wave celerity cr* versus the dimensionless wavenumber σ*. Figure 10-5 shows a plot of the primary wave logarithmic decrement -δ1 versus the dimensionless wavenumber σ*, applicable for Froude numbers F < 2. Figure 10-6 shows a plot of the primary wave logarithmic increment +δ1 versus the dimensionless wavenumber σ*, applicable for Froude numbers F > 2. Based on these figures, the characteristics of shallow waves are described in the box below.
La Figura 10-4 muestra un gráfico de la celeridad relativa adimensional de la onda cr* comparado con el número adimensionalde la onda σ*. La Figura 10-5 muestra un gráfico del decremento logarítmico de la onda primaria -δ1 en comparación con el número de onda adimensional σ*, aplicable para los números de Froude F < 2. La Figura 10-6 muestra un gráfico del incremento logarítmico de la onda primaria +δ1 en comparación con el número adimensional de onda σ*, aplicable para los números de Froude F > 2. Las características de las ondas superficiales están se describen, de acuerdo a las figuras, en el recuadro de abajo.
|
|
|
Shallow wave propagation in open-channel flow / Propagación de onda superficial en el flujo en canales 1
1 See Ponce and Simons (1977) for a detailed treatment of shallow wave propagation in open-channel flow. 1 Véase Ponce and Simons (1977) para un tratamiento detallado de propagación de la onda superficial en flujo en canales. |
10.3 KINEMATIC WAVES / ONDAS CINEMÁTICAS
|
|
A kinematic wave is an idealization (of gradually varied unsteady open-channel flow) that neglects both acceleration terms (local and convective) and the pressure-gradient term (Table 10-2). By neglecting these terms, the equation of motion (Eq. 10-14) is reduced to a statement of steady uniform flow:
Una onda cinemática es una idealización (de flujo gradualmente variado no permanente en canales) que ignora ambos términos de aceleración (local y de convección) y el término de gradiente de presión (Tabla 10-2). Al ignorar dichos términos, la ecuación de movimiento (Ec. 10.14) se reduce a un estado de flujo uniforme permanente:
|
Sf = So | (10-49) |
The unsteadiness of the phenomenon, however, is preserved through the time-varying term in the continuity equation (Eq. 10-3). The combination of Eqs. 10-3 and 10-49 gives rise to the kinematic wave equation.
Sin embargo, la inestabilidad del fenómeno se conserva a través del término que varía con el tiempo en la ecuación de continuidad (Ec. 10-3). La combinación de las Ecs. 10-3 y 10-49 da lugar a la ecuación de onda cinemática.
Since q = uh, Eq. 10-3 may be expressed in terms of the unit-width discharge:
Dado que q = uh, la Ec. 10-3 se puede expresar en términos de descarga de la unidad de ancho:
|
∂h ∂q ____ + ____ = 0 ∂t ∂x | (10-50) |
In terms of discharge Q, the continuity equation is:
La ecuación de continuidad, en términos de la descarga Q, es:
|
∂A ∂Q _____ + _____ = 0 ∂t ∂x | (10-51) |
A statement of uniform flow (Eq. 10-49) may be properly represented by the discharge-area rating:
Una expresión de flujo uniforme (Ec. 10-49) se puede representar adecuadamente mediante la relación del área de descarga:
|
Q = α A β | (10-52) |
in which α and β are coefficient and exponent, respectively. The coefficient α varies as a function of type of friction, cross-sectional shape, and bottom slope. The exponent β varies as a function of type of friction and cross-sectional shape.
en la cual α y β son el coeficiente y el exponente, respectivamente. El coeficiente α varía en función del tipo de fricción, la forma de sección transversal, y la pendiente del lecho. El exponente β varía en función del tipo de fricción y forma de la sección transversal.
Assuming for the sake of simplicity that α and β are independent of A, Eq. 10-52 yields:
Para poder simplificar se supone que α y β son independientes de A, por lo que la Ec. 10-52 se representa como sigue:
|
dQ _____ = α β A β - 1 dA | (10-53) |
|
dQ Q _____ = β ____ dA A | (10-54) |
|
dQ _____ = β V dA | (10-55) |
in which V = Q / A = mean velocity.
en la cual V = Q / A = velocidad media.
The kinematic wave equation is obtained by combining Eqs. 10-51 and 10-55 to yield:
La ecuación de onda cinemática se obtiene combinando las Ecs. 10-51 y 10-55:
|
∂Q ∂Q _____ + β V _____ = 0 ∂t ∂x | (10-56) |
In terms of unit-width discharge q :
En términos de descarga en ancho de una unidad q:
|
∂q ∂q _____ + β V _____ = 0 ∂t ∂x | (10-57) |
Convective celerity / Celeridad convectiva
Equation 10-56 (or Eq. 10-57) is a first-order partial differential equation. It describes the convection of the quantity Q (or q) with the convective velocity or celerity ck, where ck is:
La ecuación 10-56 (o Ec. 10-57) es una ecuación diferencial parcial de primer orden. Se describe la convección de la cantidad Q (or q) con la velocidad convectiva o celeridad ck, donde ck es:
|
ck = β V | (10-58) |
Given Eq. 10-55, the convective velocity may also be expressed as:
Dada la ecuación. 10-55, la velocidad convectiva también se puede expresar como:
|
dQ ck = _____ dA | (10-59) |
Given that dA = T dy (Eq. 3-11), where T = channel top width, and y = stage, the convective velocity may also be expressed as follows:
Dado que dA = T dy (Eq. 3-11), donde T = ancho superior del canal, e y = etapa, la velocidad convectiva puede también ser expresada como sigue:
|
1 dQ ck = ____ _____ T dy | (10-60) |
Equation 10-60 was originally derived by Kleitz (1877) and was later discovered from actual field observations by Seddon (1900). It often referred to as the Kleitz-Seddon Law, or simply Seddon's Law. Equation 10-58 is used when β is known with certainty, Eq. 10-59 in theoretical formulations, and Eq. 10-60 in practical applications.
La ecuación 10-60 fué derivada originalmente por Kleitz (1877) y más tarde fué descubierta por Seddon (1900) a partir de observaciones de campo. A esta ecuación se le conoce como la Ley Kleitz-Seddon, o simplemente como la ley de Seddon. La ecuación 10-58 se utiliza cuando β se conoce con certeza, la Ec. 10-59 en formulaciones teóricas, y la Ec. 10-60 en aplicaciones prácticas.
Since Eq. 10-56 is a first-order partial differential equation, it does not allow for wave diffusion (wave attenuation, or wave dissipation). Diffusion can only be obtained through the agency of a second-order term. Under the assumption of linearity (constant convective celerity), a kinematic wave will convect its discharge with no wave diffusion; that is, the discharge will retain its shape and remain constant in space and time upon propagation.
Dado que la Ec. 10-56 es una ecuación diferencial parcial de primer orden, no permite la difusión de onda (onda de atenuación, o la disipación de onda). La difusión sólo se puede obtener a través de un término de segundo orden. Bajo el supuesto de linealidad (celeridad convectiva constante), una onda cinemática conveccionará su descarga con difusión de onda nula; es decir, en la propagación, la descarga conservará su forma y permanecerá constante en el tiempo y espacio.
|
Absence of wave diffusion in the kinematic wave / La ausencia de difusión
en la onda cinemática
The absence of wave diffusion can be further demonstrated by a mathematical argument. The total derivative for Q is: La ausencia de difusión de onda puede ser demostrada de mejor forma por medio de una formulación matemática. El derivado total de Q es:
Therefore: Por lo tanto:
The kinematic wave equation is repeated here: La ecuación de onda cinemática se repite aquí:
Comparing Eq. 10-61 with Eq. 10-55, it follows that dQ/dt = 0, that is, Q remains constant in time for waves traveling with the convective celerity β V. Comparando las Ecs. 10-61 y 10-55, se deduce que dQ/dt = 0, es decir, Q permanece constante en el tiempo para las ondas que viajan con una celeridad convectiva β V. |
Kinematic shock / Choque cinemático
When the linearity assumption is relaxed, the kinematic wave may change its shape by becoming either (a) steeper [Fig. 10-7 (a)], or (b) flatter [Fig. 10-7 (b)]. Whether a wave will steepen or flatten out will depend largely on the channel cross-sectional shape. Two asymptotic limits are recognized: (1) waves propagating in hydraulically wide channels, while (2) waves propagating in inherently stable channels (Chapter 1). In hydraulically wide channels, the waves will steepen, while in inherently stable channels, they will flatten out (Ponce and Windingland, 1985).
Cuando el supuesto de linealidad no es estricto, la onda cinemática puede cambiar su forma ya sea (a) más pronunciada [Fig. 10-7 (a)], o (b) más plana [Fig. 10-7 (b)]. El hecho de que una onda sea más pronunciada o más plana dependerá en gran medida de la sección transversal del canal. Se reconocen dos límites asintóticos: (1) ondas que se propagan en canales hidráulicamente anchos, y (2) ondas que se propagan en canales inherentemente estables (Capítulo 1). En canales hidráulicamente anchos, las ondas serán más pronunciadas, mientras que en los canales inherentemente estables se aplanan (Ponce y Windingland, 1985).
|
|
When allowed to proceed unchecked, the steepening will eventually result in a kinematic wave becoming a kinematic shock. Thus, a kinematic shock is an unsteady open-channel flow feature intrinsically related to the kinematic wave: A wave must be kinematic before it can develop into a kinematic shock (Lighthill and Whitham, 1955). Kibler and Woolhiser (1970) sought to clarify the occurrence of kinematic shock phenomena by stating:
Una onda cinemática puede convertirse en un un choque cinemático, cuando el aumento de pendiente continúa sin control. Por lo tanto, un choque cinemático en un canal con flujo no permanente, es una característica intrínsecamente relacionada con la onda cinemática: Una onda debe ser cinemática antes de que pueda convertirse en un choque cinemático (Lighthill y Whitham, 1955). Kibler y Woolhiser (1970) trataron de explicar la ocurrencia de fenómenos de choque cinemático al afirmar:
|
Thus, the kinematic shock is real but rare in the physical world, where spatial irregularities manifest themselves as diffusion, with the net effect of arresting shock development. On the other hand, the computational world is likely to be much more regular, thereby inhibiting diffusion and promoting "numerical" shock development.
Por lo tanto, el choque cinemático es real pero poco común en el mundo físico, donde las irregularidades espaciales se manifiestan como difusión, con el efecto neto de la detención del desarrollo del choque. Por otra parte, es probable que sea más más común en el mundo computacaional, en donde se inhibe la difusión y se promueve el desarrollo del choque "numérico."
Kinematic wave celerity / Celeridad de la onda cinemática
The relative kinematic wave celerity, ie., the kinematic wave celerity taken relative to the flow velocity, is:
La celeridad relativa de la onda cinemática, es decir, la celeridad de la onda cinemática tomada en relación con la velocidad del flujo, es:
|
crk = (β - 1 ) V | (10-63) |
Furthermore, the dimensionless relative kinematic wave celerity is:
Además, la celeridad relativa adimensional de la onda cinemática es:
|
crk cdrk = _____ = β - 1 V | (10-64) |
According to Eq. 1-11, the relative dimensionless kinematic wave celerity is:
De acuerdo con la Ec. 1-11, la celeridad adimensional relativa de la onda cinemática es:
|
V cdrk = β - 1 = ____ F | (10-65) |
Thus, for V = 1, i.e., for neutrally stable flow, the Froude number is:
Por lo tanto, para V = 1, es decir, para el flujo neutralmente estable, el número de Froude es:
|
1 1 Fns = _______ = _______ β - 1 cdrk | (10-66) |
Table 10-3 shows the variation of: (a) the exponent β, (b) the dimensionless relative kinematic wave celerity cdrk, and (c) the neutral-stability Froude number, with selected types of friction and cross-sectional shape.
La Tabla 10-3 muestra la variación de: (a) el exponente β, (b) la celeridad de la onda relativa adimensional cinemática cdrk, y (c) el número neutral-estabilidad de Froude, con tipos de fricción y de sección transversal seleccionados.
| Table 10-3 Variation of β as a function of type of friction and cross-sectional shape. / Tabla 10-3 Variación de β como una función del tipo de fricción y de la sección transversal. | [1] | [2] | [3] | [4] | [5] | [6] |
| β | 24 β | Type of friction / Tipo de fricción | Cross-sectional shape / Sección transversal | cdrk | Fns |
| 3 | 72 | Laminar | Hydraulically wide / Hidráulicamente ancha | 2 | 1/2 |
| 8/3 | 64 | Mixed laminar-turbulent (25% turbulent Manning) / Laminar-turbulento mixto (25% Manning turbulento) | Hydraulically wide / Hidráulicamente ancha | 5/3 | 3/5 |
| 21/8 | 63 | Mixed laminar-turbulent (25% turbulent Chezy) Laminar-turbulento mixto (25% Chezy turbulento) | Hydraulically wide / Hidráulicamente ancha | 13/8 | 8/13 |
| 7/3 | 56 | Mixed laminar-turbulent (50% turbulent Manning) Laminar-turbulento mixto (50% Manning turbulento) | Hydraulically wide / Hidráulicamente ancha | 4/3 | 3/4 |
| 9/4 | 54 | Mixed laminar-turbulent (50% turbulent Chezy) Laminar-turbulento mixto (50% Chezy turbulento) | Hydraulically wide / Hidráulicamente ancha | 5/4 | 4/5 |
| 2 | 48 | Mixed laminar-turbulent (75% turbulent Manning) Laminar-turbulento mixto (75% Manning turbulento) | Hydraulically wide / Hidráulicamente ancha | 1 | 1 |
| 15/8 | 45 | Mixed laminar-turbulent (75% turbulent Chezy) Laminar-turbulento mixto (75% Chezy turbulento) | Hydraulically wide / Hidráulicamente ancha | 7/8 | 8/7 |
| 5/3 | 40 | Turbulent Manning / Manning turbulento | Hydraulically wide / Hidráulicamente ancha | 2/3 | 3/2 |
| 3/2 | 36 | Turbulent Chezy / Chezy turbulento | Hydraulically wide / Hidráulicamente anchaa | 1/2 | 2 |
| 4/3 | 32 | Turbulent Manning / Manning turbulento | Triangular | 1/3 | 3 |
| 5/4 | 30 | Turbulent Chezy / Chezy turbulento | Triangular | 1/4 | 4 |
| 1 | 24 | Any / Cualquiera | Inherently stable / Inherentemente estable | 0 | ∞ |
The following conclusions can be drawn from Table 10-3:
Las siguientes conclusiones se pueden extraer de la Tabla 10-3:
The value of the rating exponent varies from as high as β = 3 for laminar flow in a hydraulically wide channel, to as low as
β = 1 for an inherently stable channel.El valor del exponente de la curva varía de tan alta como β = 3 para el flujo laminar en un canal hidráulicamente ancho, a tan bajo como
β = 1 para un canal inherentemente estable.The value of the dimensionless relative kinematic wave celerity varies from as high as cdrk = 2 for laminar flow in a hydraulically wide channel, to as low as cdrk = 0 for an inherently stable channel.
El valor de la celeridad relativa adimensional de la onda cinemática varía de tan alta como
cdrk = 2 para el flujo laminar en un canal hidráulicamente ancho, a tan bajo como cdrk = 0 para un canal inherentemente estable.The Froude number for neutral stability varies from as low as Fns = 0.5 for laminar flow in a hydraulically wide channel (i.e., laminar overland flow), to as high as Fns = ∞ for an inherently stable channel under any type of friction (though usually turbulent).
El número de Froude para la estabilidad neutral varía desde tan bajo como Fns = 0.5 para el flujo laminar en un canal hidráulicamente ancho (es decir, el flujo superficial laminar), a tan alto como Fns = ∞ para un canal inherentemente estable bajo cualquier tipo de fricción (aunque por lo general turbulento).
The turbulent Chezy hydraulically wide dimensionless relative kinematic wave celerity is
cdrk = 0.5, confirming the results shown on (the left side of) Fig. 10-5. Thus, kinematic waves feature long wavelengths L and correspondingly "short" dimensionless wavenumbers σ* .La celeridad relativa adimensional de la onda cinemática hidráulicamente ancha de Chezy turbulento es
cdrk = 0.5, lo cual confirma los resultados mostrados en (el lado izquierdo de) la Fig. 10-5. Por lo tanto, las ondas cinemáticas tienen longitudes de onda L largas y correspondientemente números de onda adimensionales σ* "cortos".The turbulent Manning hydraulically wide dimensionless relative kinematic wave celerity is
cdrk = 2/3, i.e., the Manning value exceeds the Chezy value by 1/6.La celeridad relativa adimensional de la onda cinemática hidráulicamente ancha de Chezy turbulento es
cdrk = 2/3, , es decir, el valor de Manning supera el valor de Chezy por 1/6.
Note that the value of β may be less than 1 for cases other than those shown in Table 10-3; for example, when
the cross section does not grow monotonically with stage, as in circular culvert flow.
Also, note that since the Froude number has an upper limit
(corresponding to a realistically achievable lower limit on the bottom friction),
the value Fns = ∞ is of limited practical value.
If the maximum attainable Froude number is conservatively assumed to be
Nótese que el valor de β
puede ser inferior a 1 en
casos distintos de los que se muestran en la Tabla 3.10;
por ejemplo, cuando la sección transversal no crece
monótonamente con la etapa,
como en el flujo de alcantarilla
circular. Además, dado que el número
de Froude tiene un límite superior
(correspondiente a un
límite inferior realista alcanzable en la fricción inferior),
el valor Fns = ∞
es poco práctico.
Si se supone conservativamente que el número de Froude máximo alcanzable es
In summary, kinematic waves have the following properties:
En resumen, las ondas cinemáticas tienen las siguientes propiedades:
Kinematic waves travel with dimensionless relative wave celerity equal to 0.5, under Chezy friction; under Manning friction, the value is 2/3.
Las ondas cinemáticas viajan con una celeridad relativa adimensional de la onda igual a 0.5, bajo fricción de Chezy; bajo la fricción de Manning, el valor es 2/3.
Kinematic waves do not attenuate, but they can undergo changes in shape due to nonlinearities; in extreme cases in hydraulically wide channels, the kinematic wave may steepen to the point where it becomes a kinematic shock.
Las ondas cinemáticas no atenúan, pero pueden someterse a cambios de forma debido a no linealidades; en casos extremos de flujo en canales hidráulicamente anchos, la pendiente de la onda cinemática puede pronunciarse hasta el punto donde se convierte en un choque cinemático.
|
A word of caution regarding kinematic wave modeling / Consideraciones de precaución necesarias para modelar una onda cinemática 1
Despite the fact that wave attenuation is disavowed by kinematic wave theory, certain numerical solutions of Eq. 10-56 do exhibit a distinct attenuation. Cunge (1969) traced this apparent contradiction to the fact that numerical solutions, by virtue of their discrete grid size, introduce an error which expresses itself as numerical diffusion. As the grid is refined, the numerical effect decreases; however, a finite numerical grid (and all numerical grids are finite) will always have a residual error. A pesar del hecho de que la atenuación de la onda se rechazó por la teoría de la onda cinemática, ciertas soluciones numéricas de la Ec. 10-56 resultan en una atenuación visible. Cunge (1969) explicó que esta contradicción se debe a que en las soluciones numéricas se introduce un error, debido al tamaño de la cuadrícula, el cual se hace notar como una difusión numérica. Mientras más pequeña sea la cuadrícula o red, el efecto numérico disminuirá; sin embargo, todas las redes numéricas son finitas, por lo tanto siempre habrá un error residual. The dilemma is resolved by making the numerical diffusion simulate the physical diffusion, if any, of the physical problem. This procedure is embodied in the Muskingum-Cunge method of flood routing, described in Section 10.6. El dilema se resuelve haciendo que la difusión numérica simule la difusión física, si se presenta en el caso físico. Este procedimiento se materializa en el método de Muskingum-Cunge del tránsito de avenidas, que se describe en la Sección 10.6. 1 See Ponce (1991) for a detailed treatment of the controversy regarding kinematic waves. 1 Véase Ponce (1991) para una explicación detallada de la controversia con respecto a las ondas cinemáticas. |
Kinematic wave rating / Curva de gasto de las ondas cinemáticas
Kinematic waves are based on a single-valued discharge-area rating, Eq. 10-51. Thus, a kinematic wave rating is single-valued, exhibiting a one-to-one correspondence between (a) discharge, and (b) flow area, depth, or stage. A kinematic wave rating is calculated by using a uniform flow formula such as Manning or Chezy, for a range of (a) flow depths, in artificial channels, or (b) flow stages, in natural channels.
Las ondas cinemáticas se basan en una curva de gasto
del área de descarga de un solo valor,
Applicability of kinematic waves / Aplicabilidad de las ondas cinemáticas
A kinematic wave is a simplified type of wave, wherein three terms in the equation of motion (Table 10-2) have been either neglected or assumed to be too small to be of any practical significance. Thus, the kinematic wave does not apply to the general case. Its use is recommended for cases where the flow unsteadiness is relatively small. In practice, a kinematic wave will apply provided the following dimensionless inequality is satisfied (Ponce, 1989; Ponce, 2014):
Una onda cinemática es un tipo simplificado de onda, en el que tres términos de la ecuación de movimiento (Tabla 10-2) se ignoran debido a que son tan pequeños que son practicamente nulos. La onda cinemática no se puede aplicar como caso general. Su uso se recomienda para casos en los cuales la falta de equilibrio de flujo es relativamente pequeña. En la práctica, una onda cinemática se puede utilizar si se cumple con la siguiente desigualdad adimensional (Ponce, 1989; Ponce, 2014):
|
tr
So Vo
___________ ≥ 85 do | (10-67) |
in which tr = time-of-rise of the hydrograph, So = bottom slope, Vo = average flow velocity, and do = average flow depth.
en la cual tr = tiempo de subida del hidrograma, So = pendiente del lecho, Vo = velocidad media de flujo, y do = profundidad media del flujo.
10.4 DIFFUSION WAVES / ONDAS DE DIFUSIÓN
|
|
A diffusion wave is an idealization that neglects both acceleration terms in the equation of motion (Table 10-2). By neglecting these terms, Eq. 10-14 is reduced to the following statement:
Una onda de difusión es una idealización que ignora ambos términos de aceleración en la ecuación de movimiento (Tabla 10-2). Por lo que la Ec. 10-14 se reduce a:
|
∂h Sf = So - _____ ∂x | (10-68) |
The unsteadiness of the phenomenon, however, is preserved through the time-varying term in the continuity equation (Eq. 10-3). The combination of Eqs. 10-3 and 10-68 gives rise to the diffusion wave equation.
Sin embargo, la inestabilidad del fenómeno se conserva a través del témino que varía en el tiempo de la ecuación de continuidad (Ec. 10-3). La combinación de las Ecs. 10-3 y 10-68 da lugar a la ecuación de la onda de difusión.
The kinematic wave equation was derived by using a statement of steady uniform flow in lieu of the equation of motion (Section 10.4). In deriving the diffusion wave equation, a statement of steady nonuniform flow (friction slope is equal to water-surface slope) is used instead (Fig. 10-8). In this case, the discharge-area rating, using the Manning formula in SI Units (Eq. 5-17), is:
La ecuación de onda cinemática se derivó mediante el uso de la ecuación de flujo uniforme constante en vez de la ecuación de movimiento (Sección 10.4). Al derivar la ecuación de onda de difusión, se utiliza mejor una declaración de flujo no uniforme constante (pendiente de fricción es igual a la pendiente de la superficie del agua) (Fig. 10-8). En este caso, la curva de gasto del área de descarga, usando la fórmula de Manning en unidades de SI (Eq. 5-17), es:
|
1 dh Q = ___ A R 2/3 (So - ____ ) 1/2 n dx | (10-69) |
in which the term within parentheses (...) is the water-surface slope Sw.
en la cual el término entre paréntesis (...) es la pendiente de la superficie del agua Sw.
Figure 10-8 Diffusion wave assumption. Figure 10-8 Supuesto de la onda de difusión. |
The difference between kinematic and diffusion waves lies in the pressure-gradient term (dh/dx). When this term is included in the formulation, the resulting equation is of second order and, therefore, it is able to simulate diffusion. Lighthill and Whitham (1955) referred to this situation as the "diffusion of kinematic waves," i.e., a type of kinematic wave, still with no inertia in its formulation, that is nevertheless able to diffuse.
La diferencia entre las ondas cinemáticas y de difusión se encuentra en el término gradiente-presión (dh/dx). Cuando este término se incluye en el proceso, la ecuación resultante es de segundo orden y, por lo tanto, es capaz de simular la difusión. Lighthill and Whitham (1955) A esta situación se le conocd como la "difusión de ondas cinemáticas," es decir, un tipo de onda cinemática que, aún sin la inercia en su formulación, es capaz de difundir.
To derive the diffusion wave equation, Eq. 10-51 is repeated here in a slightly different form:
Para derivar la ecuación de onda de difusión, la Ec. 10-51 se repite a continuación con pequeños cambios:
|
∂Q ∂A _____ + _____ = 0 ∂x ∂t | (10-70) |
Equation 10-69 is expressed in a more convenient form (Cunge, 1969):
La Ecuación 10-69 se expresa en una forma más conveniente (Cunge, 1969):
|
dh m Q 2 = So - ____ dx | (10-71) |
in which m is the reciprocal of the square of the channel conveyance K (Eq. 5-34), repeated here for convenience:
en la cual m es el recíproco del cuadrado del traslado del canal K (Ec 5-34.):
|
1 K = ___ A R 2/3 n | (5-34) |
With dA = T dh, in which T = top width, Eq. 10-71 changes to:
Con dA = T dh, donde T = ancho superior, la Ec. 10-71 cambia a:
|
1 dA _____ ______ + m Q 2 - So = 0 T dx | (10-72) |
Equations 10-70 and 10-72 constitute a set of two partial differential equations describing diffusion waves. These equations can be combined into one equation with Q as dependent variable. However, it is first necessary to linearize the equations around reference flow values. For simplicity, a constant top width is assumed (i.e., a wide channel assumption).
Las ecuaciones 10-70 y 10-72 constituyen un conjunto de dos ecuaciones diferenciales parciales que describen las ondas de difusión. Estas ecuaciones se pueden combinar en una sola ecuación con Q como variable dependiente. Sin embargo, es necesario primero linealizar las ecuaciones basándose en valores de flujo de referencia. Por simplicidad, se asume un ancho superior constante (por ejemplo, se supone un canal hidráulicamente ancho).
The linearization of Eqs. 10-70 and 10-72 is accomplished by small perturbation theory (Cunge, 1969). The variables Q, A, and m can be expressed in terms of the sum of a reference value (with subscript o) and a small perturbation to the reference value (with superscript ' ): Q = Qo + Q' ; A = Ao + A' ; m = mo + m'. Substituting these into Eqs. 10-70 and 10-72, neglecting squared perturbations and subtracting the reference flow, leads to:
La linealización de las Ecs. 10-70 y 10-72 se lleva a cabo
por medio de la teoría de perturbación pequeña
(Cunge, 1969).
Las variables Q, A, y m se pueden expresar en términos de la
suma de un valor de referencia (con subíndice o) y una
perturbación pequeña al valor de referencia
(con superíndice ' ):
|
∂Q' ∂A' ____ + ____ = 0 ∂x ∂t | (10-73) |
y
|
1 ∂A' _____ ______ + Qo2 m' + 2 mo Qo Q' = 0 T ∂x | (10-74) |
Differentiating Eq. 10-73 with respect to x and Eq. 10-74 with respect to t gives:
Diferenciando la Ec. 10-73 con respecto a x y la Ec. 10-74 con respecto a t:
|
∂2Q' ∂2A' ______ + _______ = 0 ∂x 2 ∂x ∂t | (10-75) |
|
1 ∂2A' ∂m' ∂Q' _____ _________ + Qo2 _____ + 2 mo Qo ______ = 0 T ∂x ∂t ∂t ∂t | (10-76) |
Using the chain rule and Eq. 10-73 yields:
Utilizando la regla de la cadena y la Ec. 10-73 produce:
|
∂m' ∂m' ∂A' ∂m' ∂Q' _____ = _______ _______ = - ______ ______ ∂t ∂A' ∂t ∂A' ∂x | (10-77) |
Combining Eq. 10-76 with Eq. 10-77:
Combinando la Ec. 10-76 con la Ec. 10-77:
|
1 ∂2A' ∂m' ∂Q' ∂Q' _____ ________ - Qo2 ______ ______ + 2 mo Qo ______ = 0 T ∂x ∂t ∂A' ∂x ∂t | (10-78) |
Combining Eqs. 10-75 and 10-78 and rearranging terms, yields:
Combinando las Ecs. 10-75 y 10-78 y reordenando términos, se produce:
|
∂Q' Qo ∂m' ∂Q' 1 ∂Q'2 ______ - _______ ______ ______ = _____________ _______ ∂t 2 mo ∂A' ∂x 2 T mo Qo ∂x2 | (10-79) |
By definition: mQ 2 = Sf (Eq. 10-70). Therefore:
Por definición: mQ 2 = Sf (Eq. 10-70). Por lo tanto:
|
∂Q' ∂Q Qo _____ = _______ = - _______ ∂m' ∂m 2 mo | (10-80) |
y también
|
So mo Qo = ______ Qo | (10-81) |
Substituting Eqs. 10-80 and 10-81 into Eq. 10-79, using the chain rule, and dropping the superscripts for simplicity, the following equation is obtained:
Sustituyendo las Ecs. 10-80 y 10-81 en la Ec. 10-79, utilizando
la regla de la cadena, y soltando los superíndices por simplicidad,
la siguiente ecuación se obtiene:
|
∂Q ∂Q ∂Q Qo ∂2Q ______ + ( ______ ) ______ = ( _________ ) _______ ∂t ∂A ∂x 2 T So ∂x2 | (10-82) |
The left side of Eq. 10-82 is recognized as the kinematic wave equation, with ∂Q/∂A as the kinematic wave celerity.
The right side is a second-order (partial differential) term that accounts for the physical diffusion effect.
The coefficient of the second-order term has the units of diffusivity
El lado izquierdo de la Ec. 10-82 se conoce como la ecuación
de onda cinemática, donde
∂Q/∂A es la celeridad de la onda cinemática.
El lado derecho es un término de segundo orden (derivadas parciales)
que explica el efecto de difusión física.
El coeficiente del término
de segundo orden tiene las unidades de difusividad
The hydraulic diffusivity, a characteristic of the flow and channel, is defined as follows:
La difusividad hidráulica, una característica del flujo y del canal, se define como sigue:
|
Qo qo νh = _________ = _______ 2 T So 2 So | (10-83) |
in which qo = Qo /T is the reference discharge per unit of channel width. From Eq. 10-83, it is concluded that the hydraulic diffusivity is small for steep bottom slopes (e.g., those of mountain streams), and large for mild bottom slopes (e.g., those of large rivers near their mouths).
en la cual qo = Qo /T es la descarga de referencia por unidad de ancho del canal. De la Ec. 10-83, se deduce que la difusividad hidráulica es pequeña para pendientes de lecho pronunciadas (por ejemplo, las de los arroyos de montaña), y grandes para pendientes de lecho suaves (por ejemplo, de ríos grandes cerca de sus bocas).
Equation 10-82 describes the movement of flood waves in a better way than Eq. 10-50. While it falls short from describing the full inertial effects, it does physically account for wave attenuation.
La Ec. 10-82 describe el movimiento de las ondas de avenidas de mejor manera que la Ec. 10-50. A pesar de que no describe completamente los efectos de la inercia, si toma en cuenta los efectos físicos de la atenuación de la onda.
Equation 10-82 is a second-order parabolic partial differential equation. It can be solved analytically, leading to the diffusion analogy solution for flood waves (Hayami, 1951), or numerically with the aid of a numerical scheme for parabolic equations. An alternative approach is to match the hydraulic diffusivity (Eq. 10-83) with the numerical diffusion coefficient of the Muskingum flood routing method (Section 10.5). This approach is the basis of the Muskingum-Cunge method (Section 10.6).
La Ec. 10-82 es una ecuación diferencial parcial parabólica de segundo orden. Se puede resolver analíticamente, lo que lleva a la solución analógica de difusión para las ondas de avenidas (Hayami, 1951), o numéricamente con la ayuda de un esquema numérico para ecuaciones parabólicas. Alternativamente, se puede igualar la difusividad hidráulica (Ec. 10-83) con el coeficiente numérico de difusión del método del tránsito de avenidas de Muskingum (Sección 10.5). Esta propuesta es la base del método de Muskingum-Cunge (Sección 10.6).
Diffusion wave rating / Curva de gasto de la onda de difusión
Diffusion waves are not based on a single-valued discharge-area rating. Thus, a diffusion wave rating is not single-valued, exhibiting a loop. In general, however, the loop is relatively small and may be neglected on practical grounds. A kinematic wave rating may be used as an approximation in diffusion wave routing.
Las ondas de difusión no se basan en curvas de gasto del área de descarga de un solo valor. Por lo tanto, una curva de gasto de la onda de difusión no es un ciclo de un solo valor. Pero, por lo general, el ciclo es tan pequeño que por motivos prácticos se puede ignorar. Una onda cinemática se puede utilizar como una aproximación en el tránsito de ondas de difusión.
Diffusion wave celerity / Celeridad de la onda de difusión
According to Eq. 10-82, the diffusion wave celerity should be the same as the kinematic wave celerity (Ponce and Simons, 1977). However, diffusion waves attenuate; therefore, the actual discharge-area rating is not exactly single-valued. In practice, the difusion wave celerity equals the kinematic wave celerity only as an approximation.
De acuerdo con la Ec. 10-82, la celeridad de la onda de difusión debe ser la misma que la celeridad de la onda cinemática (Ponce y Simons, 1977). Sin embargo, las ondas de difusión atenúan; por lo que, la curva de gasto del área de descarga real no es de un solo valor. En la práctica, la celeridad de la onda de difusión se iguala a la celeridad de la onda cinemática para obtener únicamente una aproximación.
Applicability of diffusion waves / Aplicabilidad de las ondas de difusión
A diffusion wave is a simplified type of wave, wherein two terms in the equation of motion (Table 10-2) have been either neglected or assumed to be too small to be of any practical significance. Thus, while the diffusion wave applies for a wider range of cases than the kinematic wave, it is still not suited to the general case. Its use is recommended for cases where the flow unsteadiness is small to medium size (where the wave remains within 30% of its original strength, within one period of propagation). A diffusion wave will apply provided the following dimensionless inequality is satisfied (Ponce, 1989; Ponce, 2014):
Una onda de difusión es un tipo simplificado de onda, en el que dos términos de la ecuación de movimiento (Tabla 10-2) han sido ya sea ignorados o se suponen tan pequeños que no tienen importancia práctica. Así que a pesar que la onda de difusión se aplica para una gama más amplia de casos que la onda cinemática, aún no se puede aplicar como caso general. Se recomienda su uso para casos donde la inestabilidad del flujo es de tamaño pequeño a mediano (donde las ondas se mantienen dentro del 30% de su fuerza original, dentro de un período de propagación). Una onda de difusión se puede aplicar siempre y cuando se cumpla con la siguiente desigualdad adimensional (Ponce, 1989; Ponce, 2014):
|
g
tr So ( ____ )1/2 ≥ 15 do | (10-84) |
in which tr = time-of-rise of the hydrograph, So = bottom slope, g = gravitational acceleration, and do = average flow depth.
en la cual tr = tiempo de elevación del hidrograma, So = pendiente del lecho, g = aceleración de la gravedad, y do = profundidad media del flujo.
Diffusion waves apply to problems of flood wave propagation (see Hayami's diffusion analogy of flood waves in the box below). While kinematic waves apply to flood waves that do not diffuse, diffusion waves apply to flood waves that attenuate appreciably. Where the diffusion wave fails to account for the wave propagation, only the mixed kinematic-dynamic wave (read "dynamic wave", Table 10-2) is able to solve the problem correctly. In practice, however, diffusion waves apply to a wide range of flood propagation problems.
Las ondas de difusión se aplican a los problemas de propagación de las ondas de avenida (véase la analogía de la difusión de ondas de avenida de Hayami en el recuadro siguiente). Mientras las ondas cinemáticas se aplican a las ondas de avenidas que no se difunden, las ondas de difusión se aplican a las ondas de avenidas con atenuación notable. Debido a que la onda de difusión no toma en cuenta la propagación de la onda, solamente la onda cinemática dinámica mixta (leer "onda dinámica", Tabla 10-2) es capaz de resolver el problema correctamente. Sin embargo, en la práctica, las ondas de difusión se aplican a una amplia gama de problemas de propagación de avenidas.
|
Hayami's diffusion analogy of flood waves / Analogía de la difusión de ondas de avenida de Hayami
In 1951, Hayami published a paper entitled "On the propagation of flood waves." In it, he argued that flood waves could be modeled with a convection-diffusion equation similar to Eq. 10-82. To put it in Hayami's words: En 1951, Hayami publicó un artículo titulado "Sobre la propagación de ondas de avenida," en el que argumentó que las ondas de avenida podrían ser modelados con una ecuación de convección-difusión similar a la Ec. 10-82. Hayami lo explico de la siguiente manera:
|
Dynamic hydraulic diffusivity / Difusividad hidráulica dinámica
The hydraulic diffusivity (Eq. 10-83) is a fundamental property of diffusion waves. It states that the coefficient of diffusion is directly proportional to the unit-width discharge and inversely proportional to the channel slope. This conclusion is applicable to diffusion waves, which are governed by the convection-diffusion equation represented by Eq. 10-82.
La difusividad hidráulica (Ec. 10-83) es una propiedad fundamental de las ondas de difusión. Se afirma que el coeficiente de difusión es directamente proporcional a la descarga por unidad de ancho e inversamente proporcional a la pendiente del canal. Esta conclusión es aplicable a las ondas de difusión, las cuales se rigen por la ecuación de convección-difusión representada por la Ec. 10-82.
Using concepts of linear theory, Dooge (1973) has developed a convection-diffusion equation using the complete equation of motion. Dooge's approach extends the concept of diffusion wave to the realm of dynamic waves (Table 10-2). When all terms are included in the formulation, the hydraulic diffusivity is essentially a dynamic hydraulic diffusivity, expressed, for hydraulically wide channels, as follows:
Basándose en los conceptos de la teoría lineal,
Dooge (1973)
desarrolló una ecuación de convección-difusión utilizando
la ecuación completa de movimiento. El enfoque de Dooge
extendió el concepto de onda de difusión hacia
las ondas dinámicas (Tabla 10-2). Cuando todos los términos
se incluyen en la formulación, la difusividad hidráulica es
esencialmente una difusividad hidráulica dinámica, expresado,
para los canales de hidráulicamente anchos, como sigue:
|
qo F 2 νhF = _______ ( 1 - ______ ) 2 So 4 | (10-85) |
Ponce (1991) has expressed the dynamic hydraulic diffusivity in terms of the Vedernikov number, as follows:
Ponce (1991) ha expresado la difusividad
hidráulica dinámica en términos del número de Vedernikov, como sigue:
|
qo νhV = _______ ( 1 - V 2 ) 2 So | (10-86) |
Unlike Eq. 10-85, Eq. 10-86 is not limited to hydraulically wide channels, being applicable to channels of any cross-sectional shape.
A diferencia de la Ec. 10-85, la Ec. 10-86 no se limita exclusivamente a los canales hidráulicamente anchoss, por el contrario, se puede aplicar a canales de cualquier sección transversal.
Equation 10-86 is altogether better than Eq. 10-83. They are equivalent only if V = 0, i.e., for very small Froude-number flows. For V = 1, using Eq. 10-86, the hydraulic diffusivity vanishes, while this is not the case for Eq. 10-83, for which the hydraulic diffusivity remains finite.
La Ecuación 10-86 es una mejor solución que la Ec. 10-83. Estas ecauciones son equivalentes sólo si V = 0, es decir, para flujos con números de Froude muy pequeños. Cuando se utiliza la Ec. 10-86 con V = 1, la difusividad hidráulica se anula, lo cual no ocurre con la Ec. 10-83 (la difusividad hidráulica sigue siendo finita).
10.5 MÉTODO DE MUSKINGUM
|
|
The Muskingum method of flood routing was developed in connection with the design of flood protection schemes in the Muskingum River Basin, Ohio (Fig. 10-10) (McCarthy, 1938). It is the most widely used method of flood routing, with numerous applications in the United States and throughout the world.
El método de Muskingum del tránsito de avenidas fue desarrollado en relación con el diseño de los planes de protección de avenidas en la cuenca del Río Muskingum, Ohio (Fig. 10-10) (McCarthy, 1938). Es el método más utilizado para el tránsito de avenidas, con numerosas aplicaciones en los Estados Unidos y en todo el mundo.
Figure 10-10 The Muskingum river near Marietta, Ohio. / El Río Muskingum cerca de Marietta, Ohio. |
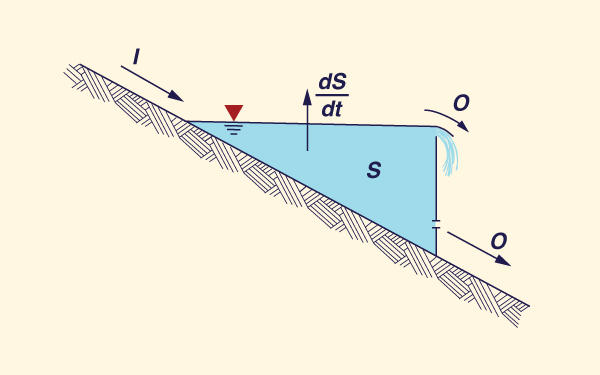
The method is based on the differential equation of storage (Fig. 10-11):
El método se basa en la ecuación diferencial de almacenamiento (Fig 10-11.):
|
dS I - O = _____ dt | (10-87) |
in which I = inflow, O = outflow, and S = storage.
en la cual I = entrada, O = salida, y S = almacenamiento.
Figure 10-11 Definition sketch for inflow, outflow, and storage in a reservoir.
Figure 10-11 Esquema para la entrada, la salida y |
In an ideal channel, storage is a function of inflow and outflow. This is in constrast with an ideal reservoir, in which storage is solely a function of outflow. In the Muskingum method, storage is a linear function of inflow and outflow:
En un canal ideal, el almacenamiento es una función del flujo de entrada y el flujo de salida. Comparativamente, en un reservorio ideal, el almacenamiento es únicamente una función del flujo de salida. En el método de Muskingum, el almacenamiento es una función lineal de entrada y salida:
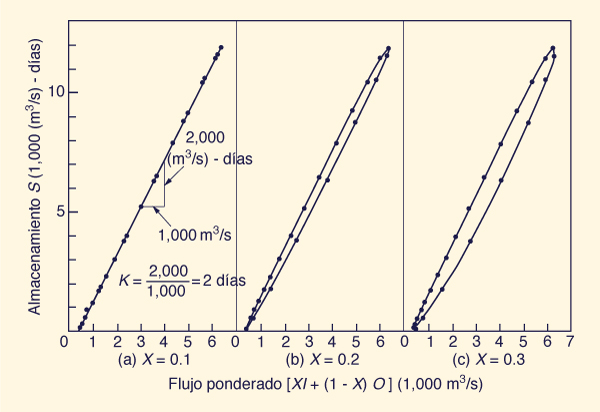
| S = K [ X I + ( 1 - X ) O ] | (10-88) |
in which S = storage volume; I = inflow; O = outflow; K = a time constant or storage coefficient; and
en la cual S = volumen de almacenamiento; I = flujo de entrada;
O = flujo de salida;
K = una constante de tiempo o un coeficiente de almacenamiento;
y
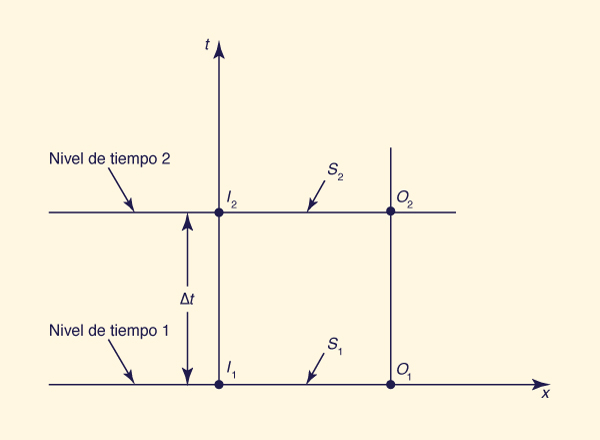
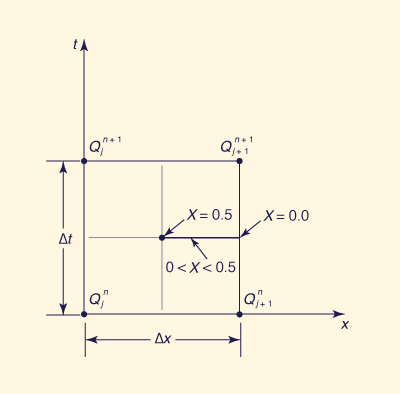
To derive the Muskingum routing equation, Eq. 10-87 is discretized on the x-t plane (Fig. 10-12), to yield:
Para derivar la ecuación de tránsito de Muskingum, la Ec. 10-87 se discretiza en el plano x-t (Fig 10-12.), para producir:
|
I1 + I2 O1 + O2 S2 - S1 __________ - ___________ = ___________ 2 2 Δt | (10-89) |
Figure 10-12 Discretization on the x-t plane. Figure 10-12 Discretización en el plano x-t. |
Equation 10-88 is expressed at time levels 1 and 2:
La Ecuación 10-88 se expresa en los niveles de tiempo 1 y 2:
| S1 = K [ X I1 + ( 1 - X ) O1 ] | (10-90) |
| S2 = K [ X I2 + ( 1 - X ) O2 ] | (10-91) |
Substituting Eqs. 10-90 and 10-91 into Eq. 10-89 and solving for O2 yields:
Sustituyendo las Ecs. 10-90 y 10-91 en la Ec. 10-89 y resolviendo para O2 se produce:
| O2 = C0 I2 + C1 I1 + C2 I1 | (10-92) |
in which C0, C1 and C2 are routing coefficients defined in terms of Δt, K, and X as follows:
en la cual C0, C1 and C2 son coeficientes de tránsito definidos en términos de Δt, K, y X como sigue:
|
( Δt / K ) - 2X C0 = _______________________ 2(1 - X) + ( Δt / K ) | (10-93a) |
|
( Δt / K ) + 2X C1 = _______________________ 2(1 - X) + ( Δt / K ) | (10-93b) |
|
2(1 - X) - ( Δt / K ) C2 = _______________________ 2(1 - X) + ( Δt / K ) | (10-93c) |
Since C0 + C1 + C2 = 1, the routing coefficients may be interpreted as weighting coefficients.
Dado que C0 + C1 + C2 = 1, los coeficientes de tránsito pueden ser interpretados como coeficientes de ponderación.
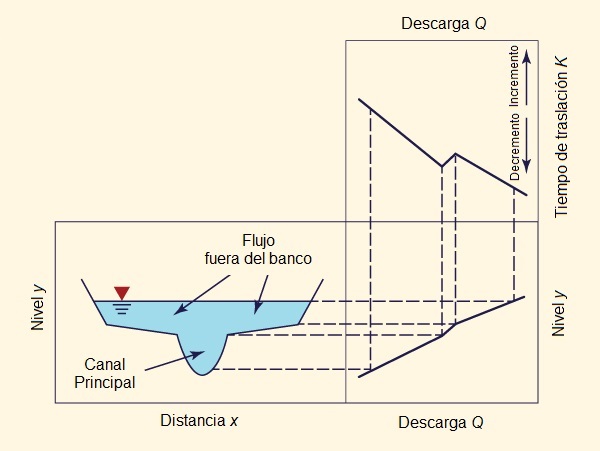
Given an inflow hydrograph, an initial flow condition, a chosen time interval Δt, and routing parameters X and K, the routing coefficients can be calculated with Eq. 10-93, and the outflow hydrograph with Eq. 10-92. The routing parameters K and K are related to flow and channel characteristics, K being interpreted as the travel time of the flood wave from upstream end to downstream end of the channel reach. Therefore, K accounts for the translation portion of the routing (Fig. 10-12).
Dado un hidrograma de entrada, con condición de flujo inicial, con intervalo de tiempo elegido Δt, y con parámetros de tránsito X y K, los coeficientes de tránsito se pueden calcular con la Ec. 10-93, y el hidrograma de salida con la Ec. 10-92. Los parámetros de tránsito X y K están relacionados con las características del flujo y del canal, K se interpreta como el tiempo de viaje de la onda de avenidas del extremo aguas arriba al extremo aguas abajo del canal. Por lo tanto, K representa la porción de la traducción del tránsito (Fig. 10-12).
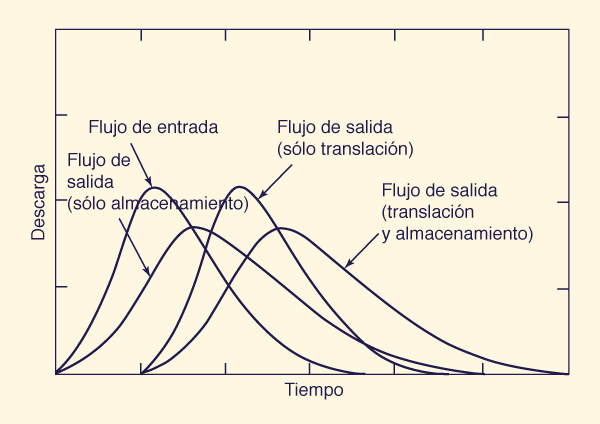
The parameter X accounts for the storage portion of the routing. For a given flood event, there is a value of X for which the storage in the calculated outflow hydrograph matches that of the measured outflow hydrograph. The effect of storage is to reduce the peak flow and spread the hydrograph in time (Fig. 10-13). Therefore, it is often used interchangeably with the terms diffusion and peak attenuation.
El parámetro X representa la porción de almacenamiento del tránsito. Para cierto evento de avenidas, hay un valor de X para el cual el almacenamiento en el hidrograma de salida calculado coincide con la del hidrograma de salida medido. El efecto del almacenamiento es reducir el flujo máximo y difundir el hidrograma en el tiempo (Fig. 10-13). Por lo tanto, se utiliza a menudo de manera intercambiable con los términos de difusión y la atenuación pico.
Figure 10-13 Translation and storage processes in stream channel routing. Figure 10-13 Procesos de traslado y almacenamiento en el tránsito de arroyo. |
The routing parameter K is a function of channel reach length and flood wave speed; conversely, the parameter X is a function of the flow and channel characteristics that cause runoff diffusion. In the Muskingum method, X is interpreted as a weighting factor and restricted in the range 0 ≤ X ≤ 0.5. Values of X greater than 0.5 produce hydrograph amplification (i.e., negative diffusion), which does not correspond with reality (under the Froude numbers applicable to flood flows). With K = Δt and X = 0.5, flow conditions are such that the outflow hydrograph retains the same shape as the inflow hydrograph, but it is translated downstream a time equal to K. For X = 0, Muskingum routing reduces to linear reservoir routing.
El parámetro de tránsito K es una función de la longitud del
tramo del canal y la velocidad de la onda de avenida; por el contrario,
el parámetro X es una función de las características de flujo y
del canal que causan la difusión de escorrentía. En el método
de Muskingum, X se interpreta como un factor de ponderación y
es restringido al intervalo 0 ≤ X ≤ 0.5.
Los valores de X mayores
que 0.5 producen una amplificación del hidrograma (es decir, una difusión
negativa), que no corresponde con la realidad
(bajo los números de Froude aplicables a los flujos de avenidas).
Cuando K = Δt y
In the Muskingum method, the parameters K and X are determined by calibration using streamflow records. Simultaneous inflow-outflow discharge measurements for a given channel reach are coupled with a trial-and-error procedure, leading to the determination of K and X (see Example 10-1). The procedure is time-consuming and lacks predictive capability. Values of K and X determined in this way are valid only for the given reach and flood event used in the calibration. Extrapolation to other reaches or to other flood events (of different magnitude) within the same reach is usually unwarranted.
En el método de Muskingum, los parámetros K y X se determinan por calibración usando registros de caudal. Las mediciones del caudal de entrada-salida de flujo simultáneas para un tramo del canal dado son se emparejan con un procedimiento de prueba y error, lo que lleva a la determinación de K y X (véase el Ejemplo 10-1). El procedimiento es lento y carece de capacidad de predicción. Los valores de K y X así determinados son válidos sólo para el tramo dado y el evento de avenidas utilizado en la calibración. La extrapolación a otros tramos o para otros eventos de avenidas (de diferente magnitud) dentro del mismo tramo suele ser injustificada.
When sufficient data are available, a calibration can be performed for several flood events, each of different magnitude, to cover a wide range of flood levels. In this way, the variation of K and X as a function of flood level can be ascertained. In practice, K is more sensitive to flood level than X. A sketch of the variation of K with stage and discharge is shown in Fig. 10-14.
Cuando se dispone de datos suficientes, la calibración se puede realizar por varios eventos de avenidas, cada una de diferente magnitud, para cubrir una amplia gama de niveles de avenidas. De esta manera, la variaci&oacue;n de K y X en función del nivel de avenidas puede ser comprobada. En la práctica, K es más sensible al nivel de avenidas que X. Un esquema de la variación de K con la etapa y la descarga se muestra en la Fig. 10-14.
Figure 10-14 Sketch of travel time as a function of discharge and stage. Figure 10-14 Esquema del tiempo de viaje en función de la descarga y la etapa. |
Ejemplo 10-1.
An inflow hydrograph to a channel reach is shown in Col. 2 of Table 10-4.
Assume baseflow is 352 m3/s.
Using the Muskingum method, route this hydrograph through a channel reach with K = 2 d and X = 0.1 to calculate an outflow hydrograph.
Un hidrograma de entrada a un tramo del canal se muestra
en la Col. 2 de la Tabla 10-4. Supongamos que la base de flujo del canal es de
352 m3/s. Utilizando el método de Muskingum, haga el tránsito de este
hidrograma a través de un tramo de canal con
K = 2 d y X = 0.1 para
calcular un hidrograma de salida.
First, it is necessary to select a time interval Δt.
In this case, it is convenient to choose Δt = 1 d.
As with reservoir routing, the ratio of time-to-peak to time interval
(tp /Δt ) should be greater than or equal to 5.
In addition, the chosen time interval should be such that the routing coefficients remain positive.
With Δt = 1 d, K = 2 d, and X = 0.1, the routing coefficients (Eq. 10-93) are: C0 = 0.1304; C1 = 0.3044; and C2 = 0.5652.
It is verified that C0 + C1 + C2 = 1.
The routing calculations are shown in Table 10-4.
En primer lugar, es necesario seleccionar un intervalo de tiempo
Δt.
En este caso, es conveniente elegir Δt = 1 d.
Como con el tránsito del
reservorio, el gasto de la curva de tiempo-pico al intervalo de tiempo
(tp /Δt )
debe ser mayor que o igual a 5.
Además, el intervalo de tiempo elegido
debe ser tal que los coeficientes de tránsito siguen siendo positivos.
Con Δt = 1 d, K = 2 d, y X = 0.1, los coeficientes de tránsito
(Ec. 10-93)
son: C0 = 0.1304; C1 = 0.3044; y C2 = 0.5652.
Se verifica que C0 + C1 + C2 = 1.
Los cálculos de tránsito se muestran en la Tabla 10-4.
Column 1 shows the time in days.
La Columna 1 muestra el tiempo en días.
Column 2 shows the inflow hydrograph ordinates in cubic meters per second.
La columna 2 muestra las ordenadas del hidrograma de flujo de entrada en metros cúbicos
por segundo.
Columns 3-5 show the partial flows.
Las Columnas 3-5 muestran los flujos parciales.
Following Eq. 10-91, Cols. 3-5 are summed to obtain Col. 6, the outflow hydrograph ordinates in cubic meters per second.
Siguiendo la Ec. 10-91, Cols. 3-5 se suman para obtener la Col. 6,
las ordenadas del hidrograma de salida en metros cúbicos por segundo.
To explain the procedure briefly, the outflow at the start (day 0) is assumed to be equal to the inflow at the start: 352 m3/s. The inflow at day 1 multiplied by C0 is entered in Col. 3, day 1: 76.6 m3/s.
The inflow at day 0 multiplied by C1 is entered in Col. 4, day 1: 107.1 m3/s.
The outflow at day 0 multiplied by C2 is entered in Col. 5, day 1: 199 m3/s.
Columns 3-5 of day 1 are summed to obtain Col. 6 of day 1: 76.6 + 107.1 + 199.0 = 382.7 m3/s.
The calculations proceed in a recursive manner until all outflows in Col. 6 have been obtained.
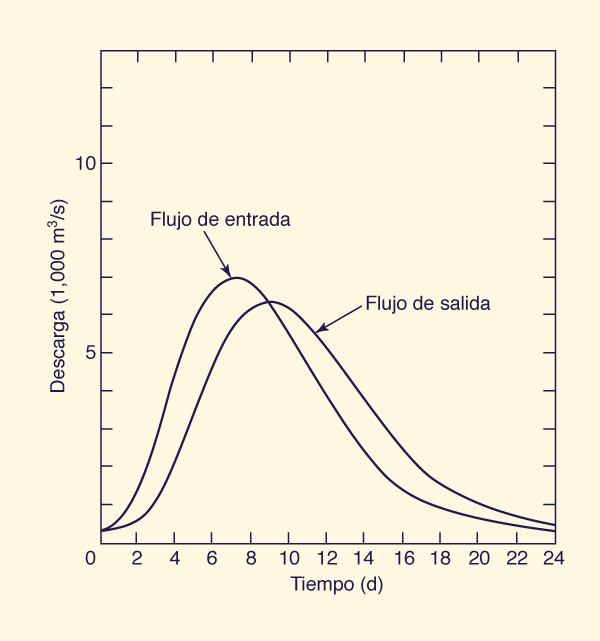
Inflow and outflow hydrographs are plotted in Fig. 10-15.
The outflow peak is 6352.6 m3/s, which shows that the inflow peak, 6951 m3/s, has attenuated to about 91 % of its initial value.
The peak outflow occurs at day 9, 2 d after the peak inflow, which occurs at day 7.
The time elapsed between the occurrence of peak inflow and peak outflow is generally equal to K, the travel time.
Para explicar brevemente el procedimiento, el flujo de salida
en el inicio (día 0) se supone que es igual que la entrada de flujo en
el inicio:
352 m3/s. La entrada de flujo en el día 1 multiplicado
por C0 se introduce en la Col. 3, día 1: 76.6 m3/s.
La entrada de flujo en el día 0 multiplicado por
C1 se introduce
en la Col. 4, día 1: 107.1 m3/s.
La salida en el día 0
multiplicado por C2 se introduce en la Col. 5, día 1: 199 m3/s.
Columnas 3-5 del día 1 se suman para obtener Col. 6 del día 1: 76.6 + 107.1 + 199.0 = 382.7 m3/s.
Los cálculos se realizan de manera recursiva hasta que se hayan
obtenido todas las salidas de flujo en la Col. 6.
Los hidrogramas de entrada y salida de flujo se representan en la Fig. 10-15.
El pico de salida de flujo es 6352.6 m3/s,
lo que demuestra que el pico de entrada de flujo, 6951 m3/s, ha atenuado
hasta alrededor de 91% de su valor inicial.
El flujo de salida del
pico se produce en el día 9, 2 dias después que el flujo de entrada pico,
el cual se produce en el día 7. El tiempo transcurrido entre la ocurrencia
de flujo de entrada pico y flujo de salida pico es generalmente igual a K, el tiempo de viaje.
Figure 10-15 Stream channel routing by Muskingum method:
Figure 10-15 TrÁNsito de canal mediante el método
ONLINE CALCULATION.
Using ONLINE ROUTING04, the answer
is essentially the same as that of Col. 6, Table 10-4.
CÁLCULO EN LÍNEA.
Usando ONLINE ROUTING04,
la respuesta es esencialmente la misma que la de la Col. 6, Tabla 10-4.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Example 10-1 has illustrated the predictive stage of the Muskingum method, in which the routing parameters are known in advance of the routing. If the parameters are not known, it is first necessary to perform a calibration. The trial-and-error procedure to calibrate the routing parameters is illustrated by Example 10-2.
El Ejemplo 10-1 ha ilustrado la etapa de predicción del método de Muskingum, en el que los parámetros de tránsito se conocen de anteman. Si no se conocen los parámetros, primero es necesario realizar una calibración. El procedimiento de prueba y error para calibrar los parámetros de tránsito se ilustra mediante el Ejemplo 10-2.
Ejemplo 10-2.
Use the outflow hydrograph calculated in the previous example together with the given
inflow hydrograph to calibrate the Muskingum method, that is, to find the routing parameters K and X.
Utilice el hidrograma de salida de flujo calculado en el ejemplo anterior,
junto con el hidrograma de entrada de flujo dado para calibrar el método
de Muskingum, es decir, para encontrar los parámetros de tránsito
K y X.
The procedure is summarized in Table 10-5.
El procedimiento se resume en la Tabla 10-5.
Column 1 shows the time in days.
La columna 1 muestra el tiempo en días.
Column 2 shows the inflow hydrograph in cubic meters per second.
La columna 2 muestra el hidrograma de entrada de flujo en metros cúbicos por segundo.
Column 3 shows the outflow hydrograph in cubic meters per second.
La columna 3 muestra el hidrograma de salida de flujo en metros cúbicos por segundo.
Column 4 shows the channel storage in (cubic meters per second)-days.
La columna 4 muestra el almacenamiento del canal en (metros cúbicos por segundo) -días.
Channel storage at the start is assumed to be 0, and this value is entered in Col. 4, day 0.
Almacenamiento del canal en el inicio se supone que es 0,
y este valor se introduce en la Col. 4, día 0.
Channel storage is calculated by solving Eq. 10-89 for S2:
Almacenamiento del canal se calcula mediante la resolución de la Ec. 10-89 para
S2:
Several values of X are tried, within the range 0.0 to 0.5, for example, 0.1, 0.2 and 0.3.
Varios valores de X se prueban, dentro del rango de 0.0 a 0.5, por ejemplo, 0.1, 0.2 y 0.3.
For each trial value of X, the weighted flows [ XI + ( 1 - X ) O ] are calculated, as shown in Cols. 5-7.
Para cada valor de prueba de X, los flujos ponderados
[ XI + ( 1 - X ) O ]
se calculan, como se muestra en Cols. 5-7.
Each of the weighted flows is plotted against channel storage (Col. 4), as shown in Fig. 10-16.
Cada uno de los flujos ponderados se representa junto
al canal de almacenamiento (Col. 4), como se muestra en la Fig. 10-16.
The value of X for which the storage versus weighted flow data plots closest to a line is taken as the correct value of X.
In this case, Fig. 10-16 (a): X = 0.1 is chosen.
El valor de X para el cual el almacenamiento en comparación
del dato del flujo ponderado se grafica más cerca a la línea se toma
como el valor correcto de X.
En este caso, se selecciona X = 0.1, como muestra la Fig. 10-16 (a):
Following Eq. 10-88, the value of K is obtained from Fig. 10-16 (a) by calculating the slope of the storage vs weighted outflow curve.
Siguiendo la Ec. 10-88, el valor de K se obtiene a partir de la Fig. 10-16 (a) mediante el
cálculo de la pendiente de almacenamiento vs la curva de salida de flujo ponderado.
In this case, the value of K = [2000 (m3/s)-d]/(1000 m3/s) = 2 d.
En este caso, el valor de K = [2,000 (m3/s)-d]/(1000 m3/s) = 2 d.
Thus, it is shown that K = 2 days and X = 0.1 are the Muskingum routing parameters for the given inflow and outflow hydrographs.
Por lo tanto, se muestra que K = 2 días y X = 0.1 son los parámetros
de tránsito Muskingum para los hidrogramas de entrada de flujo y salida de flujo dados.
Figure 10-16 Calibration of Muskingum routing parameters: Example 10-2.
Figure 10-16 Calibración de los parámetros de tránsito Muskingum: Ejemplo 10-2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The estimation of routing parameters is crucial to the application of the Muskingum method. The parameters are not constant, tending to vary with flow rate. If the routing parameters can be related to flow and channel characteristics, the need for trial-and-error calibration would be eliminated. Parameter K could be related to reach length and flood wave velocity, whereas X could be related to the diffusivity characteristics of flow and channel. These propositions are the basis of the Muskingum-Cunge method.
La estimación de parámetros de tránsito es crucial para la aplicación del método de Muskingum. Los parámetros no son constantes y tienden a variar con la velocidad de flujo. Si los parámetros de tránsito pudieran relacionarse con el flujo y las características del canal, no fuera necesaria la calibración por prueba y error. El parámetro K podría estar relacionado con la longitud del tramo y la velocidad de onda de avenidas, mientras que X podría estar relacionado con las características de difusividad de flujo y el canal. Estas propuestas son la base del método de Muskingum-Cunge.
10.6 MÉTODO DE MUSKINGUM-CUNGE
|
|
The Muskingum method requires a calibration in order to identify the routing parameters (Example 10-2). The procedure is based on measured input and output hydrographs, as shown in Cols. 2 and 3 of Table 10-5. Therefore, a gaging station is an absolute necessity for the Muskingum method to be properly used. This limits the applicability of the method to reaches which have a streamgaging station.
El método Muskingum requiere una calibración con el fin de identificar los parámetros de tránsito (Ejemplo 10-2). El procedimiento se basa en hidrogramas de entrada y salida de flujo medidos, como se muestra en Cols. 2 y 3 de la Tabla 10-5. Por lo tanto, una estación de aforo es una necesidad absoluta para que el método de Muskingum sea utilizado correctamente. En otras palabras, el método puede ser utilizado únicamente en tramos del canal que tengan una estación de aforo.
Unlike the Muskingum method, the Muskingum-Cunge method requires hydraulic rather than hydrologic data in order to calculate the routing parameters. The hydraulic data consists of geomorphic data such as channel slope and cross-sectional characteristics. Thus, the Muskingum-Cunge method does not explicitly require a streamgaging station, being applicable to any channel reach as long as the geomorphic data is available.
A diferencia del método de Muskingum, el método Muskingum-Cunge requiere de información hidráulica en vez de hidrológica para calcular los parámetros de tránsito. El dato hidráulico consta de datos geomorfológicos tales como la pendiente del canal y características de la sección transversal. Por lo tanto, el método de Muskingum-Cunge no requiere explícitamente una estación de aforo del canal, por lo que se puede aplicar a cualquier tramo del canal siempre y cuando haya información geomorfológica disponible.
The Muskingum method is derived by combining the differential equation of storage, i.e., the continuity equation expressed in total differential form (Eq. 10-87) with a linear inflow-outflow-storage relation (Eq. 10-88). This leads to the Muskingum routing equation (Eq. 10-92) with appropriate routing coefficients (Eq. 10-93). The Muskingum-Cunge method is derived by discretizing the kinematic wave equation (Eq. 10-55) in a linear mode, in a manner similar to that of the Muskingum method, which leads to the same routing equation. The coefficients, however, are defined based on measurable channel characteristics.
El método de Muskingum se deriva mediante la combinación de la ecuación diferencial de almacenamiento, es decir, la ecuación de continuidad expresada en forma diferencial total (Ec. 10-87) con una relación lineal de entrada-salida-almacenamiento (Ec. 10-88). Esto conduce a la ecuación de tránsito de Muskingum (Ec. 10-92) con coeficientes de tránsito apropiados (Ec. 10-93). El método Muskingum-Cunge se deriva por la discretización de froma lineal de la ecuación de onda cinemática (Ec. 10-55), de una manera similar a la del método de Muskingum, lo cual conduce a la misma ecuación de tránsito. Sin embargo, los coeficientes se definen en base a las características medibles del canal.
The similarities appear to end there. The Muskingum method is lumped across the channel reach, based on storage, and able to describe flood wave diffusion (Example 10-1). The Muskingum-Cunge method is distributed, with data specified at cross sections, and based on a discretization of the kinematic wave equation, which ostensibly does not diffuse. Yet actual calculations using the Muskingum-Cunge method shows that it is able to describe wave diffusion, in a manner similar to the Muskingum method.
Los puntos descritos anteriormente son las únicas simililtudes entre los dos métodos. El método de Muskingum se agrupa a través del tramo del canal, basandose en el almacenamiento, y la capacidad de describir la difusión de la onda de avenida (Ejemplo 10-1). El método de Muskingum-Cunge se distribuye, con los datos especificados en las secciones transversales, y se basa en una discretización de la ecuación de la onda cinemática, que aparentemente no se difunde. Sin embargo, los cálculos reales utilizando el método de Muskingum-Cunge demuestra que es capaz de describir la difusión de onda, de una manera similar al método de Muskingum.
Cunge (1969) traced the diffusion of the discretized analog of the kinematic wave equation to the numerical diffusion of the scheme itself (see box). Thus, he was able to explain the paradox. The Muskingum and Muskingum-Cunge methods have the same theoretical basis. The routing parameters of the Muskingum method are hydrologic, based on storage, and determined by calibration using streamflow data. The routing parameters of the Muskingum-Cunge method are hydraulic, distributed (at a cross section), and based exclusively on geomorphic data.
Cunge (1969) trazó la difusión del análogo discretizada de la
ecuación de onda cinemática a la difusión numérica del propio
régimen (véase el recuadro). Por lo tanto, fué capaz de explicar
la contradicción. Los métodos de Muskingum y Muskingum-Cunge tienen
la misma base teórica. Los parámetros de tránsito del método
de Muskingum son hidrológicos, basados en almacenamiento, y determinados
por la calibración utilizando datos de flujo. Los parámetros
de tránsito del método de Muskingum-Cunge son hidráulicos,
distribuidos (en una sección transversal), y basados exclusivamente en
datos geomorfológicos.
|
A word of explanation on the concept of numerical diffusion / Breve explicación del concepto de difusión numérica 1
The existence of diffusion in a numerical scheme needs further elaboration. As Hayami (1951) pointed out, in nature irregularities produce physical diffusion. The same process extends to the computational world: Irregularities produce numerical diffusion. The irregularities are interpreted as the errors inherent to the numerical computation, among which the truncation errors stand out primordially. The replacement of a partial differential equation, based on ∂, with a finite difference equation, based on Δ, results in errors, which, when taken in the aggregate, manifest themselves as diffusion. Thus, numerical diffusion is in the computational world what physical diffusion is in the real world. La existencia de difusión en un esquema numérico requiere de una mayor elaboración mas profunda. Hayami (1951) señaló, que en la naturaleza las irregularidades producen difusión física. El mismo proceso se extiende al mundo computacional: Las irregularidades producen difusión numérica. Las irregularidades se interpretan como los errores inherentes al cálculo numérico, entre los que los errores de truncamiento destacan primordialmente. La sustitución de una ecuación diferencial parcial, basada en ∂, con una ecuación diferencial finita, basada en Δ, produce errores, que, cuando se toman en conjunto, se manifiestan como difusión. Por lo tanto, la difusión numérica es al mundo computacional lo que la difusión física es al mundo real. 1 See Cunge (1969) for a detailed treatment of numerical diffusion in connection with the Muskingum method. 1 Véase Cunge (1969) para una explicación detallada de difusión numérica en relación con el método de Muskingum. |
Muskingum-Cunge routing equation / Ecuación de tránsito de Muskingum-Cunge
To derive the Muskingum-Cunge routing equation, the kinematic wave equation (Eq. 10-55) is discretized on the x-t plane (Fig. 10-17) in a way that parallels the Muskingum method, centering the spatial derivative and off-centering the temporal derivative by means of a weighting factor X:
Para derivar la ecuación de tránsito Muskingum-Cunge,
la ecuación de onda cinemática
|
X (Q j n+1 - Q j n ) + (1 - X) (Q j+1n+1 - Q j+1 n ) ________________________________________________ + Δt |
|
(Q j+1 n - Q j n ) + (Q j+1n+1 - Q
j n+1 ) c _______________________________________ = 0 2 Δx | (10-94) |
in which c = βV is the kinematic wave celerity.
en la cual c = βV es la celeridad de la onda cinemática.
Figure 10-17 Space-time discretization of the kinematic wave equation
Figure 10-17 Discretización del espacio-tiempo de la ecuación de |
Solving Eq. 10-94 for the unknown discharge leads to the following routing equation:
Resolviendo la Ec. 10-94 para la descarga desconocida conduce a la siguiente ecuación de avenida:
| Q j+1 n+1 = C0 Q j n+1 + C1 Q j n + C2 Q j+1 n | (10-95) |
The routing coefficients are:
Los coeficientes de tránsito son:
|
c ( Δt / Δx ) - 2X C0 = ________________________ 2(1 - X) + c ( Δt / Δx ) | (10-96a) |
|
c ( Δt / Δx ) + 2X C1 = ________________________ 2(1 - X) + c ( Δt / Δx ) | (10-96b) |
|
2(1 - X) - c ( Δt / Δx ) C2 = ________________________ 2(1 - X) + c ( Δt / Δx ) | (10-96c) |
By defining the travel time as
Al definir el tiempo de viaje como
|
Δx K = ______ c | (10-97) |
it is seen that the sets of Eq. 10-93 and Eq. 10-96 are the same.
como es puede ver, los conjuntos de la Ec. 10-93 y la Ec. 10-96 son los mismos.
Equation 10-97 confirms that K is in fact the flood wave travel time, i.e., the time it takes a given discharge to travel the reach length Δx with the kinematic wave celerity c.
La Ecuación 10-97 confirma que K es de hecho el tiempo de viaje de
la onda de avenidas, es decir, el tiempo que tarda una descarga
dada a viajar a lo largo del tramo Δx con la celeridad de la onda cinemática
c.
Numerical properties / Propiedades numéricas
The Courant number is defined as the ratio of physical celerity (c) to the numerical, or grid, celerity
El número de Courant se define como la relación de celeridad física
(c) a la numérica, o red, celeridad
|
Δt C = c ______ Δx | (10-98) |
Equation 10-95 is a numerical analog of Eq. 10-55 and, therefore, subject to numerical diffusion and dispersion. Numerical diffusion is the second-order error; numerical dispersion is the third-order error. The following conditions hold:
La Ecuación 10-95 es un análogo numérico de la Ec. 10-55 y, por lo tanto, es sujeta a difusión y dispersión numéricas. La difusión numérica es el error de segundo orden; la dispersión numérica es el error de tercer orden. Las siguientes condiciones se cumplen:
For X = 0.5 and C = 1, the routing equation is third-order accurate, i.e., the numerical solution is equal to the analytical solution (of the kinematic wave equation).
Para X = 0.5 y C = 1, la ecuación de avenida tiene precisión de tercer orden, es decir, la solución numérica es igual a la solución analítica (de la ecuación de onda cinemática).
For X = 0.5 and C ≠ 1, the routing equation is second-order accurate, exhibiting only numerical dispersion.
Para X = 0.5 y C ≠ 1, la ecuación de avenidad tiene precisión de segundo orden, exhibiendo solamente la dispersión numérica.
For X < 0.5 and C ≠ 1, the routing equation is first-order accurate, exhibiting both numerical diffusion and dispersion.
Para X < 0.5 y C ≠ 1, la ecuación de avenida es tiene precisión de primer orden, exhibiendo ambas: difusión y dispersión numéricas.
For X < 0.5 and C = 1, the routing equation is first-order accurate, exhibiting only numerical diffusion.
Para X < 0.5 and C = 1, la ecuación de avenida tiene presición de primer orden, exhibiendo solamente la difusión numérica.
These relations are summarized in Table 10-6.
Estas relaciones se resumen en la Tabla 10-6.
| ||||||||||||||||||||||||||||||
In practice, the numerical diffusion can be used to simulate the physical diffusion of the actual flood wave. By expanding the discrete function Q (jΔx, n Δt) in Taylor series about grid point (jΔx, n Δt), the numerical diffusion coefficient of the Muskingum scheme is derived (Cunge, 1969) (Appendix B):
En la práctica, la difusión numérica puede ser utilizada para simular la difusión física de la onda de avenidas actual. Con la ampliación de la función discreta Q (jΔx, n Δt) en serie de Taylor alrededor del punto de cuadrícula (jΔx, n Δt), se deriva el coeficiente de difusión numérico del esquema de Muskingum (Cunge, 1969) (Apéndice B):
|
1 νn = c Δx ( ____ - X ) 2 | (10-99) |
in which νn is the numerical diffusion coefficient of the Muskingum scheme. This equation reveals the following:
en el cual νn es el coeficiente de difusión numérico del esquema de Muskingum. Esta ecuación revela lo siguiente:
For X = 0.5 there is no numerical diffusion, although there is some numerical dispersion for
C ≠ 1; Para X = 0.5 no hay difusión numérica, aunque hay cierta dispersión numérica para
C ≠ 1; For X > 0.5, the numerical diffusion coefficient is negative, i.e., numerical amplification, which explains the behavior of the Muskingum method for this range of X values;
Para X > 0.5, el coeficiente de difusión numérico es negativo, es decir, existe amplificación numérica, lo que explica el comportamiento del método de Muskingum para esta gama de valores de X;
For Δx = 0, the numerical diffusion coefficient is zero, clearly the trivial case.
Para Δx = 0, el coeficiente de difusión numérico es cero, claramente el caso trivial.
A predictive equation for X can be obtained by matching the hydraulic diffusivity νh (Eq. 10-83) with the numerical diffusion coefficient of the Muskingum scheme νn (Eq. 10-99). This leads to the following expression for X:
Se puede obtener una ecuación de predictiva para X al igualar la difusividad hidráulica νh (Eq. 10-83) con el coeficiente de difusión numérico del esquema de Muskingum νn (Eq. 10-99). Esto conduce a la siguiente expresión para X:
|
1 qo X = ___ ( 1 - __________ ) 2 So c Δx | (10-100) |
With X calculated by Eq. 10-100, the Muskingum method is referred to as Muskingum-Cunge method. Thus, the routing parameter X can be calculated as a function of the following numerical and physical properties:
Cuando se calcula X por medio de la Ec. 10-100, el método de Muskingum se conoce como método de Muskingum-Cunge. Por lo tanto, el parámetro de avenida X se puede calcular como una función de las siguientes propiedades numéricas y físicas:
Reach length Δx,
Longitud del tramo Δx,
Reference discharge per unit width qo,
Descarga de referencia por unidad de ancho qo,
Kinematic wave celerity c, and
Celeridad de la onda cinemática c, y
Bottom slope / Pendiente del lecho So.
It should be noted that Eq. 10-100 was derived by matching physical and numerical diffusion (a second-order processes), and does not account for dispersion (a third-order process). Therefore, in order to simulate wave diffusion properly with the Muskingum-Cunge method, it is necessary to optimize numerical diffusion (with Eq. 10-100) while at the same time minimizing numerical dispersion by keeping the value of C ≅ 1.
Cabe señalar que la Ec. 10-100 se deriva haciendo coincidir la difusión física con la numérica (un proceso de segundo orden), y no toma en cuenta la dispersión (un proceso de tercer orden). Por lo tanto, con el fin de simular la difusión de onda con el método de Muskingum-Cunge correctamente, es necesario optimizar la difusión numérica (con la Ec. 10-100), y a la vez, minimizar la dispersión numérica manteniendo el valor de C ≅ 1.
|
Advantage of the Muskingum-Cunge method / Ventaja del método de Muskingum-Cunge
A unique feature of the Muskingum-Cunge method, which sets it apart from other numerical kinematic wave models, is the grid independence of the calculated outflow hydrograph.
If numerical dispersion is minimized, the calculated outflow at the downstream end of a channel reach will be essentially the same, regardless of how many subreaches are used in the computation.
This is because X is a function of Δx,
and the routing coefficients C0, C1,
and
Una característica única del método de Muskingum-Cunge,
que lo diferencía de otros modelos de ondas cinemáticas
numéricas, es la independencia de la cuadrícula del hidrograma calculado para el flujo de salida. Si se reduce al mínimo la dispersión numérica,
la salida de flujo calculada en el extremo inferior de un tramo del canal
será esencialmente el mismo, independientemente del número de
subtramos utilizados en el cálculo. Esto es porque
X es una función
de Δx, y los coeficientes de tránsito
C0, C1,
y |
An improved version of the Muskingum-Cunge method is due to Ponce and Yevjevich (1978). The grid diffusivity is defined as the numerical diffusivity for the case of X = 0. From Eq. 10-99, the grid diffusivity is:
Ponce and Yevjevich (1978) ofrecen una versión mejorada del método de Muskingum-Cunge. La difusividad de la malla se define como la difusividad numérica para el caso de X = 0. A partir de la Ec. 10-99, la difusividad de malla es:
|
Δx νg = c _____ 2 | (10-101) |
The cell Reynolds number D is defined as the ratio of hydraulic diffusivity (Eq. 10-83) to grid diffusivity (Eq. 10-101). This leads to:
La célula del número de Reynolds D se define como la relación de la difusividad hidráulica (Ec. 10-83) a la difusividad de la malla (Ec. 10-101). Esto lleva a:
|
qo D = __________ So c Δx | (10-102) |
Therefore:
Por lo tanto:
|
1 X = ___ ( 1 - D ) 2 | (10-103) |
Equations 10-101 and 10-102 imply that for very small values of Δx, D may be greater than 1, leading to negative values of X. In fact, for the characteristic reach length
Las Ecuaciones 10-101 y 10-102 implican que para valores muy pequeños de Δx, D puede ser mayor que 1, conduciendo a valores negativos de X. De hecho, para la características de la longitud del tramo
|
qo Δxc = ________ So c | (10-104) |
the cell Reynolds number is D = 1, and X = 0. Therefore, in the Muskingum-Cunge method, reach lengths shorter than the characteristic reach length result in negative values of X. This should be contrasted with the classical Muskingum method (Section 10.4), in which X is restricted in the range 0.0 ≤ X ≤ 0.5. In the classical Muskingum, X is interpreted as a weighting factor. As shown by Eqs. 10-101 and 10-102, nonnegative values of X are associated with long reaches, typical of the manual computation used in the development and early application of the Muskingum method.
la celda del número de Reynolds es D = 1, y X = 0. Por lo tanto, en el método de Muskingum-Cunge, las longitudes del tramo más cortas que la longitud característica del tramo resulta en valores negativos de X. Esto se compara con el método de Muskingum clásico (Sección 10.4 ), en el cual X se encuentra dentro del rango de 0.0 ≤ X ≤ 0.5. En el Muskingum clásico, X se interpreta como un factor de ponderación. Las Ecs. 10-101 y 10-102 muestran que los valores no negativos de X están asociados con tramos largos, típicos del cálculo manual utilizado en el desarrollo y las primeras aplicaciones del método de Muskingum.
In the Muskingum-Cunge method, however, X is interpreted in a moment-matching sense or diffusion-matching factor. Therefore, negative values of X are entirely possible. This feature allows the use of shorter reaches than would otherwise be possible if X were restricted to nonnegative values.
Sin embargo, en el método de Muskingum-Cunge, X se interpreta como un factor de igualación de momento o como factor de equidad de difusión Por lo tanto, los valores negativos de X son posibles. Esta característica permite el uso de tramos más cortos lo cual no sería posible si X se limitara a valores no negativos.
Routing coefficients / Coeficientes de tránsito
The substitution of Eqs. 10-98 and 10-100 into Eq. 10-96 leads to routing coefficients expressed in terms of Courant and cell Reynolds numbers:
La sustitución de las Ecs. 10-98 y 10-100 en la Ec. 10-96 conduce a coeficientes de tránsito expresados en términos de n&uacut;meros de Courant y de Reynolds de la malla:
|
-1 + C + D C0 = ______________ 1 + C + D | (10-105a) |
|
1 + C - D C1 = ______________ 1 + C + D | (10-105b) |
|
1 - C + D C2 = ______________ 1 + C + D | (10-105c) |
The calculation of routing parameters C and D can be performed in several ways. The wave celerity can be calculated with either Eq. 10-57 or Eq. 10-59. With Eq. 10-57, c = βV; with Eq. 10-59, c = (1/T) dQ/dy. Theoretically, these two equations are the same. For practical applications, if a stage-discharge rating and cross-sectional geometry are available (i.e., stage-discharge-top width tables), Eq. 10-59 is preferred over Eq. 10-57 because it accounts directly for cross-sectional shape. In the absence of a stage-discharge rating and cross-sectional data, Eq. 10-57 can be used to estimate flood wave celerity.
El cálculo de los parámetros de tránsito C and D se puede realizar de varias maneras. La celeridad de la onda se puede calcular ya sea con la Ec. 10-57 o la Ec. 10-59. Con la Ec. 10-57, c = βV; con la Ec. 10-59, c = (1/T) dQ/dy. Teóricamente, estas dos ecuaciones son iguales. Para aplicaciones prácticas, si se cuenta con la información de la curva de gasto del nivel-caudal y de la geometría de la sección transversal (es decir, curva de descarga-profundidad-ancho), se prefiere la Ec. 10-59 sobre la Ec. 10-57, ya que la primera considera de forma directa la forma de la sección transversal. La Ec. 10-57 se utiliza para estimar la celeridad de la onda de avenidas cuando no se cuenta con los datos de una curva de gasto del nivel-caudal y de la sección transversal.
With the aid of Eqs. 10-98 and 10-102, the routing parameters may be based on flow characteristics. The calculations can proceed in a linear or nonlinear mode. In the linear mode, the routing parameters are based on reference flow values and kept constant throughout the computation in time. The choice of reference flow has a bearing on the calculated results, although the overall effect is likely to be small (Ponce and Yevjevich, 1978). For practical applications, either an average or peak flow value can be used as reference flow. The peak flow value has the advantage that it can be readily ascertained, although a better approximation may be obtained by using an average value. The linear mode of computation is referred to as the constant-parameter Muskingum-Cunge method to distinguish it from the variable-parameter Muskingum-Cunge method, in which the routing parameters are allowed to vary with the flow. The constant parameter method resembles the Muskingum method, with the difference that the routing parameters are based on measurable flow and channel characteristics instead of on historical streamflow data.
Con la ayuda de las Ecs. 10-98 y 10-102, los parámetros de tránsito pueden basarse en las características de flujo. Los cálculos pueden proceder de modo lineal o no lineal. En el modo lineal, los parámetros de tránsito se basan en valores del flujo de referencia y se mantienen constantes durante el cálculo en el tiempo. La elección de flujo de referencia tendrá efecto en los resultados calculados, aunque es probable que el impacto global sea pequeño (Ponce and Yevjevich, 1978). Para aplicaciones prácticas, se puede utilizar ya sea un valor promedio de flujo o un flujo pico como valor de referencia. El valor de flujo máximo tiene la ventaja de que se puede determinar fácilmente, pero se puede ser obtener una mejor aproximación mediante el uso de un valor medio. El cálculo lineal se conoce como el método de Muskingum-Cunge de parámetro constante para distinguirlo del método de Muskingum-Cunge de parámetro variable, en el cual los parámetros de tránsito pueden variar con el flujo. El método del parámetro constante se asemeja al método de Muskingum, con la diferencia de que los parámetros de tránsito se basan en el flujo medible y las características del canal en lugar de los datos históricos del flujo.
Ejemplo 10-3.
Use the constant-parameter Muskingum-Cunge method to route a flood wave with the following flood and channel characteristics: peak flow Qp = 1000 m3/s; baseflow Qb, = 0 m3/s; channel bottom slope So =
0.000868; flow area at peak discharge Ap = 400 m2; top width at peak discharge Tp = 100 m;
rating exponent β = 1.6; reach length Δx = 14.4 km; time interval Δt = 1 h.
Utilice el método de Muskingum-Cunge
de parámetro constante para hacer el tránsito de la onda de avenidas
con los siguientes flujos y
características del canal:
flujo de avenida:
Qp = 1000 m3/s; flujo
de base Qb, = 0 m3/s;
pendiente del fondo del canal So =
0.000868;
área del flujo en la descarga máxima
The mean velocity (based on the peak discharge) is V = Qp/Ap = 2.5 m/s.
The wave celerity is c = βV =
La velocidad media (basada en la descarga máxima) es
V = Qp/Ap = 2.5 m/s. La celeridad de la onda es
ONLINE CALCULATION.
Using ONLINE ROUTING05, the answer
is essentially the same as that of Col. 6, Table 10-7.
CÁLCULO EN LÍNEA.
Usando ONLINE ROUTING05, la respuesta es esencialmente
la misma que la de la Col. 6, Tabla 10-7.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Resolution requirements / Requisitos de resolución
When using the Muskingum-Cunge method, care should be taken to ensure that the values of Δx and Δt are sufficiently small to approximate closely the actual shape of the hydrograph. For smoothly rising hydrographs, a minimum value of tp /Δt = 5 is recommended. This requirement usually results in the hydrograph time base being resolved into at least 15 to 25 discrete points, considered adequate for Muskingum routing.
Cuando se utiliza el método de Muskingum-Cunge, es necesario asegurar que los valores de Δx and Δt sean lo suficientemente pequeños para asegurar una buena aproximación a la forma real del hidrograma. Se recomienda un valor mínimo de tp /Δt = 5, para aquellos hidrogramas que crecen lentamente. Este requisito usualmente da como resultado que el tiempo del hidrograma se resuelva en por lo menos 15 a 25 puntos discretos, lo cualse considera adecuado para el tránsito de Muskingum.
Unlike temporal resolution, there is no definite criteria for spatial resolution. A criterion borne out by experience is based on the fact that Courant and cell Reynolds numbers are inversely related to reach length Δx. Therefore, to keep Δx sufficiently small, Courant and cell Reynolds numbers should be kept sufficiently large. This leads to the practical criterion (Ponce and Theurer, 1982):
A diferencia de la resolución temporal, no hay criterios definidos para la resolución espacial. Un criterio confirmado por la experiencia se basa en el hecho de que los números de Courant y de Reynolds de la malla están inversamente relacionados a la longitud del tramo Δx. Por lo tanto, para mantener Δx suficientemente pequeña, los números de Courant y de Reynolds de la malla se deben mantener suficientemente grandes. Esto conduce al criterio práctico (Ponce y Theurer, 1982):
| C + D ≥ 1 | (10-106) |
which can be written as follows: -1 + C + D ≥ 0. This confirms the necessity of avoiding negative values of C0 in Muskingum-Cunge routing (see Eq. 10-105a). Experience has shown that negative values of either C1 or C2 do not adversely affect the method's overall accuracy.
la cual se puede escribir como sigue: -1 + C + D ≥ 0. Esto confirma la necesidad de evitar valores negativos de C0 en el tránsito de Muskingum-Cunge (ver la Ec. 10-105a.). La experiencia ha demostrado que los valores negativos de cualquiera de C1 o C2 no afecten negativamente a la precisión global del método.
Notwithstanding Eq. 10-106, the Muskingum-Cunge method works best when the numerical dispersion is minimized, that is, when C ≅ 1. Values of C substantially less than 1 are likely to cause the notorious dips, or negative outflows, in portions of the calculated hydrograph. This computational anomaly is attributed to excessive numerical dispersion and should be avoided.
No obstante la Eq. 10-106, el método de Muskingum-Cunge funciona mejor cuando la dispersión numérica se minimiza, es decir, cuando C ≅ 1. Es probable que los valores de C sustancialmente menores que 1 causen las caídas notorias, o salidas de flujo negativas, en porciones del hidrograma calculado. Esta anomalía computacional se atribuye a la dispersión numérica excesiva y debe ser evitada.
Nonlinear Muskingum-Cunge method / Método de Muskingum-Cunge no lineal
The kinematic wave equation, Eq. 10-55, is nonlinear because the kinematic wave celerity varies with discharge. The nonlinearity is mild, among other things because the wave celerity variation is usually restricted within a narrow range. However, in certain cases it may be necessary to account for this nonlinearity. This can be done in two ways: (1) during the discretization, by allowing the wave celerity to vary, resulting in a nonlinear numerical scheme to be solved by iterative means; and (2) after the discretization, by varying the routing parameters, as in the variable-parameter Muskingum-Cunge method (Ponce and Yevjevich, 1978). The latter approach is particularly useful if the overall nonlinear effect is small, which is often the case.
La ecuación de onda cinemática, la Ec. 10-55, es no lineal debido a que la celeridad de la onda cinemática varía con la descarga. La no linealidad es leve, entre otras cosas porque la variación de la celeridad de onda se restringe generalmente dentro de un rango estrecho. Sin embargo, en ciertos casos puede ser necesario tomar en cuenta esta no linealidad. Esto se puede hacer de dos maneras: (1) durante la discretización, al permitir que la celeridad de la onda varíe, lo que resulta en un esquema numérico no lineal el cual se resuelve por medios iterativos; y (2) después de la discretización, mediante la variación de los parámetros de tránsito, como en el método de Muskingum-Cunge de parámetro variable (Ponce y Yevjevich, 1978). El segundo enfoque es particularmente útil si el efecto no lineal general es pequeño, lo cual a menudo es el caso.
The variable parameter Muskingum-Cunge method represents a small yet sometimes perceptible improvement over the constant parameter method. The differences are likely to be more marked for very long reaches and/or wide variations in flow levels. Flood hydrographs calculated with variable parameters show a certain amount of distortion, either wave steepening in the case of flows contained inbank or wave attenuation (flattening) in the case of typical overbank flows. This is a physical manifestation of the nonlinear effect, i.e., different flow levels traveling with different celerities. On the other hand, flood hydrographs calculated using constant parameters do not show wave distortion.
El método de Muskingum-Cunge de parámetro variable presenta una pequeña y en veces perceptible mejora sobre el método de parámetro constante. Las diferencias son probablemente más marcadas en tramos muy largos y / o grandes variaciones en los niveles de flujo. Los hidrogramas de avenidas calculados con parámetros variables muestran una cierta cantidad de distorsión, ya sea de empinamiento de onda en el caso de los flujos contenidos dentro del banco u onda de atenuación (aplanamiento) en el caso de los flujos de desbordamientos típicos. Esta es una manifestación física del efecto no lineal, es decir, diferentes niveles de flujo viajando con diferentes celeridades. Por el contrario, los hidrogramas de avenidas calculados utilizando los parámetros constantes no muestran distorsión de la onda.
Assessment of Muskingum-Cunge method / Evaluación del método de Muskingum-Cunge
The Muskingum-Cunge method is a physically based alternative to the Muskingum method. Unlike the Muskingum method where the parameters are calibrated using streamflow data, in the Muskingum-Cunge method the parameters are calculated based on flow and channel characteristics. This makes possible channel routing without the need for time-consuming and cumbersome parameter calibration. More importantly, it makes possible extensive channel routing in ungaged streams with a reasonable expectation of accuracy. With the variable-parameter feature, nonlinear properties of flood waves (which could otherwise only be obtained by more elaborate numerical procedures) can be described within the context of the Muskingum formulation.
El método de Muskingum-Cunge es una alternativa de base física para el método de Muskingum. A diferencia del método de Muskingum donde los parámetros son calibrados usando los datos del canal, en el método de Muskingum-Cunge los parámetros se calculan basándose en las características del flujo y del canal. Esto hace posible el tránsito del canal sin necesidad de calibración de parámetro engorroso y que toma mucho tiempo. Más importante aún, hace posible de manera extensa el tránsito de canal en arroyos de corrientes no aforadas con una expectativa razonable de precisión. Con la característica de parámetro variable, las propiedades no lineales de ondas de avenidas (las cuales de otro modo sólo se pueden obtener por procedimientos numéricos más elaborados) pueden describirse en el contexto de la formulación Muskingum.
Like the Muskingum method, the Muskingum-Cunge method is limited to diffusion waves. Furthermore, the Muskingum-Cunge method is based on a single-valued rating and does not take into account strong flow non-uniformity or unsteady flows exhibiting substantial loops in discharge-stage rating (i.e., dynamic waves). Thus, the Muskingum-Cunge method is suited for channel routing in natural streams without significant backwater effects and for unsteady flows that classify under the diffusion wave criterion (Eq. 10-66).
Al igual que el método de Muskingum, el método Muskingum-Cunge se limita a las ondas de difusión. Además, el método de Muskingum-Cunge se basa en una curva de gasto de valor único y no toma en cuenta la falta de uniformidad de un flujo fuerte ni los flujos inestables que muestran círculos sustanciales en la curva de gasto de descarga-profundidad (es decir, ondas dinámicas). Por lo tanto, el método de Muskingum-Cunge es adecuado para el tránsito del canal en los arroyos naturales y sin efectos significativos de remanso y para flujos inestables que se pueden clasificar bajo el criterio de onda de difusión (Ec. 10- 66).
An important difference between the Muskingum and Muskingum-Cunge methods should be noted. The Muskingum method is based on the storage concept (Eq. 10-87) and, therefore, it is lumped, with the parameters K and X being reach averages. The Muskingum-Cunge method, however, is distributed in nature, with the parameters C and D being based on values evaluated at channel cross sections. Therefore, for the Muskingum-Cunge method to improve on the Muskingum method, it is necessary that the routing parameters evaluated at channel cross sections be representative of the channel reach under consideration (Fig. 10-18).
Cabe señalar una diferencia importante entre los métodos de Muskingum y Muskingum-Cunge. El método Muskingum se basa en el concepto de almacenamiento (Ec. 10-87) y, por lo tanto, se agrupa, y los parámetros K y X son los promedios de los tramos. El método de Muskingum-Cunge, sin embargo, tiene una naturaleza de distribución, y sus parámetros C and D se basan en los valores evaluados en secciones transversales del canal. Por lo tanto, para que el método de Muskingum-Cunge se mejore en base al método de Muskingum, es necesario que los parámetros de tránsito evaluadas en secciones transversales de los canales sean representativos del tramo del canal en cuestión (Fig. 10-18).
Historically, the Muskingum method has been calibrated using streamflow data. On the contrary, the Muskingum-Cunge method relies on physical characteristics such as rating curves, cross-sectional data and channel slope. The different data requirements reflect the different theoretical bases of the methods, i.e., lumped storage concept in the Muskingum method, and distributed kinematic/diffusion wave theory in the Muskingum-Cunge method.
Históricamente, el método de Muskingum ha sido calibrado usando datos de caudal. Por el contrario, el método Muskingum-Cunge se basa en las características físicas, tales como curvas de gasto, los datos de secciones transversales y pendiente del canal. Los diferentes requisitos de datos reflejan las diferentes bases teóricas de los métodos, es decir, el concepto de almacenamiento agrupado en el método de Muskingum, y la teoría de la onda cinemática / difusión distribuída en el método Muskingum-Cunge.
Figure 10-18 Moyan river, Lambayeque, Peru. Figura 10-18 Río Moyán, Lambayeque, Perú. |
10.7 DYNAMIC WAVES / ONDAS DINÁMICAS
|
|
In unsteady open-channel flow, the term dynamic wave is used to refer to two different types of waves:
En el flujo de canal no permanente, el término onda dinámica se utiliza para referirse a dos tipos diferentes de ondas:
A wave that neglects the friction and bottom slope, that is, wave [3] in Table 10-2, and
Una onda que no considera la fricción ni la pendiente del lecho, es decir, la onda [3] en la
Tabla 10-2, yA wave that includes all terms in the equation of motion, that is, wave [5] in Table 10-2.
Una onda que incluye todos los términos de la ecuación de movimiento, es decir, la onda [5] en la Tabla 10-2.
To avoid confusion, the first type of wave [3] is referred here as true dynamic wave. The second type [5] is referred to as mixed kinematic-dynamic wave, for short, mixed dynamic wave.
Para evitar confusión, el primer tipo de onda [3] se conoce aquí como onda dinámica verdadera. El segundo tipo [5] se denomina como onda cinemática-dinámica mixta, y se abrevia como onda dinámica mixta.
True dynamic waves / Ondas dinámicas verdaderas
Conceptually, true dynamic waves are the exact opposite of kinematic waves. While kinematic waves lie to the left side of the wavenumber spectrum, true dynamic waves lie to the right (Fig. 10-3). Thus, their dimensionless wavenumber is long, that is, the wavelength L is short relative to the reference channel length Lo (Eq. 10-30).
Conceptualmente, las ondas dinámicas verdaderas son exactamente contrarias a las ondas cinemáticas. Mientras las ondas cinemáticas se encuentran al lado izquierdo del espectro de número de onda, las ondas dinámicas verdaderas se encuentran a la derecha (Fig. 10-3). Por lo tanto, su número de onda adimensional es largo, es decir, la longitud de onda L es corta en relación a la longitud de referencia del canal Lo (Eq. 10-30).
While the dimensionless relative celerity of a kinematic wave is constant and equal to 0.5, that of the true dynamic wave is equal to the reciprocal of the Froude number (Fig. 10-3):
Mientras que la celeridad relativa adimensional de una onda cinemática es constante e igual a 0.5, la de la onda dinámica verdadera es igual a la inversa del número de Froude (Fig 10-3.):
|
1 (gho)1/2 cdrd = ____ = _________ F uo | (10-107) |
The relative celerity of a true dynamic wave is:
La celeridad relativa de una onda dinámica verdadera es:
|
crd = (gho)1/2 | (10-108) |
The celerity of a true dynamic wave is:
La celeridad de una onda dinámica verdadera es:
|
crd = uo ± (gho)1/2 | (10-109) |
Therefore, a true dynamic wave has two components, with celerities:
Por lo tanto, una onda dinámica verdadera tiene dos componentes, y sus celeridades son:
|
crd1 = uo + (gho)1/2 | (10-110) |
|
crd2 = uo - (gho)1/2 | (10-111) |
Kinematic and true dynamic waves share a distinct property: They do not attenuate. This is due to the constancy of the dimensionless relative wave celerity within the applicable range of dimensionless wavenumbers (Fig. 10-3).
Las ondas cinemáticas y dinámicas verdaderas comparten una característica distintiva: no se atenúan. Esto se debe a la constancia de la celeridad de la onda relativa adimensional dentro de la gama aplicable de números de onda adimensionales (Fig. 10-3).
In practice, true dynamic waves apply to the "short" waves that may be present in laboratory flumes and small canals. They do not apply for flood waves, which lie on the left side of the dimensionless wavenumber spectrum.
En la práctica, las ondas dinámicas verdaderas se aplican a las ondas "cortas" que puedan estar presentes en canales de laboratorio y pequeños canales. No se aplican en las ondas de avenidas, que se encuentran en el lado izquierdo del espectro del número de onda adimensional.
Mixed dynamic waves / Ondas dinámicas mixtas
Mixed kinematic-dynamic waves lie toward the middle of the wavenumber spectrum (Fig. 10-3). Conceptually, they are the most complete type of wave, because they consider all the terms in the equation of motion (Table 10-2). However, for Vedernikov numbers V < 1, (corresponding to Froude numbers F < 2 under Chezy friction in hydraulically wide channels), the mixed waves are subject to strong attenuation. The attenuation is strongest at the point of inflexion of the dimensionless relative celerity versus dimensionless wavenumber function (Fig. 10-3). Figure 10-4 shows the attenuation rates as described by the logarithmic decrement δ.
Las ondas cinemáticas dinámicas mixtas se encuentran hacia el centro del espectro del número de onda (Fig. 10-3). Conceptualmente, son el tipo más completo de onda, ya que consideran todos los términos de la ecuación de movimiento (Tabla 10-2). Sin embargo, para los números de V < 1, (correspondiente a los números de Froude F < 2 bajo la fricción Chezy en canales hidráulicamente anchos), las ondas mixtas están sujetas a una atenuación fuerte. La atenuación es más fuerte en el punto de inflexión de la celeridad relativa adimensional contra la función del número de onda adimensional (Fig. 10-3). La Figura 10-4 muestra las tasas de atenuación descritas por el decremento logarítmico δ.
Lighthill and Whitham (1955) described the impermanence of dynamic waves in the following terms:
Lighthill y Whitham (1955) describen la impermanencia de las ondas dinámicas de la siguiente manera:
"In the case of flood waves, kinematic and dynamic waves are both possible together. However, the dynamic waves have both a much higher wave velocity and also a rapid attenuation. Hence, although any disturbance sends some signal downstream at the ordinary wave velocity for long gravity waves (sic), this signal is too weak to be noticed at any considerable distance downstream, and the main signal arrives in the form of a kinematic wave at a much slower velocity."
"En el caso de las ondas de avenidas, se pueden presentar ambas ondas cinemáticas y dinámicas al mismo tiempo. Sin embargo, las ondas dinámicas tienen tanto una velocidad de onda mucho más alta y también una atenuación rápida. Por lo tanto, a pesar de cualquier perturbación envía alguna señal aguas abajo en la velocidad de la onda ordinaria a lo largo de las ondas de gravedad (sic), esta señal es demasiado débil para ser notado en cualquier distancia considerable aguas abajo, y la señal principal llega en la forma de una onda cinemática a una velocidad mucho más lenta".
They followed up with this statement (op. cit., page 291):
Siguieron con esta declaración (op. cit., página 291):
"We have thought it desirable to give a mathematical treatment of the 'competition' between kinematic and dynamic waves in river flow, in order to show how completely the dynamic waves are subordinated in the case of greatest interest, that is, when the speed of the river is well subcritical. This demonstrates the unsuitability of the characteristics of the dynamic wave as the basis for computation."
"Hemos creído conveniente ofrecer un tratamiento matemático de la 'competencia' entre las ondas cinemáticas y dinámicas en el caudal de los ríos, con el fin de mostrar completamente cómo las ondas dinámicas están subordinados en el caso de mayor interés, es decir, cuando la velocidad del río es subcrítico. Esto demuestra que la base del cálculo es la falta de adaptación de las características de la onda dinámica."
Thus, in general, mixed dynamic waves do not apply to flood flows in natural streams. Once generated, dynamic waves tend to dissipate very quickly, with their mass going to join the predominant underlying kinematic or kinematic-with-diffusion (diffusion) wave.
Así, en general, las ondas dinámicas mixtas no se aplican a los flujos de avenidas en los arroyos naturales. Una vez generadas, las ondas dinámicas tienden a disiparse rápidamente, y su masa se une a la onda cinemática o cinemática-con-difusión (difusión) subyacente predominante.
The exception may be a flood wave generated by a dam breach, which is typically so sudden that it may actually be a mixed dynamic wave. These waves attenuate very quickly, confirming the correctness of the theory. For example, consider the failure of Teton Dam, in Idaho, on June 5, 1976 (Fig. 10-19). The flood wave released at the damsite attenuated to a small fraction of its initial strength within a relatively short distance downstream. Many other examples of actual dam breaches have confirmed that dam-breach flood waves tend to dissipate rather quickly.
La excepción puede ser una onda de avenida generada por una rotura de presa, la cual típicamente es tan repentina que en realidad puede ser una onda dinámica mixta. Estas ondas se atenúan muy rápido, lo que confirma la exactitud de la teoría. Por ejemplo, considere el falla de la Presa de Teton, en Idaho, el 5 de Junio de 1976 (Fig. 10-19). La onda de avenida lanzada en el sitio de la presa se atenuó a una pequeña fracción de su fuerza inicial dentro de una distancia relativamente corta aguas abajo. Muchos otros ejemplos de roturas de presas actuales han confirmado que las ondas de avenida de la rotura de la presa tienden a disiparse con mucha rapidez.
Figure 10-19 El fallo de la presa de Teton, Idaho, 5 de Junio de 1976. |
Modeling of mixed dynamic waves / Modelado de las ondas dinámicas mixtas
In a dynamic wave solution, the equations of continuity and motion are solved by a numerical procedure, either (a) the method of finite differences, (b) the method of characteristics, or (c) the finite element method. In the method of finite differences, the partial differential equations are discretized following a chosen numerical scheme. The method of characteristics is based on the conversion of the set of partial differential equations into a related set of ordinary differential equations, and the solution along a characteristic grid, i.e. a grid that follows characteristic directions. The method of finite elements solves a set of integral equations over a chosen grid of finite elements.
En una solución de la onda dinámica, las ecuaciones de continuidad y movimiento se resuelven mediante un procedimiento numérico, ya sea (a) el método de diferencias finitas, (b) el método de características, o (c) el método de elementos finitos. En el método de las diferencias finitas, las ecuaciones diferenciales parciales se discretizan siguiendo un esquema numérico elegido. El método de las características se basa en la conversión del conjunto de ecuaciones diferenciales parciales a un conjunto relacionado de ecuaciones diferenciales ordinarias, y la solución a lo largo de una malla característica, es decir, una malla que sigue direcciones características. El método de los elementos finitos resuelve un sistema de ecuaciones integrales sobre una malla elegida de elementos finitos.
In the past four decades, the method of finite differences has come to be regarded as the most expedient way of obtaining a (mixed) dynamic wave solution for practical applications. Among several numerical schemes that have been used in connection with the dynamic wave, the Preissmann scheme is perhaps the most popular (Liggett and Cunge, 1975). This is a four-point scheme, centered in the temporal derivatives and slightly off-centered in the spatial derivatives, by use of a weighting factor θ. The off-centering in the spatial derivatives introduces a small amount of numerical diffusion necessary to control the numerical stability of the nonlinear scheme. This produces a workable yet sufficiently accurate scheme.
En las últimas cuatro décadas, el método de las diferencias finitas ha llegado a ser considerada como la forma más conveniente de obtener una solución de onda dinámica (mixta) para aplicaciones prácticas. Entre varios esquemas numéricos que se han utilizado en relación con la onda dinámica, el esquema Preissmann es quizás el más popular (Liggett y Cunge, 1975). Este es un esquema de cuatro puntos, centrado en los derivados temporales y ligeramente descentrada en las derivadas espaciales, mediante el uso de un factor de ponderación θ. el hecho de que las derivadas espaciales no se encuentren justamente en el centro introduce una pequeña cantidad de difusión numérica la cual es necesaria para controlar la estabilidad numérica del esquema no lineal. Esto produce un esquema viable con precisión aceptable.
The independent variables used in (mixed) dynamic wave routing are usually discharge Q and
Las variables independientes utilizadas en el tránsito de onda
dinámica mixta son generalmente la descarga Q y el
Figure 10-20 Reach subdivision for dynamic wave routing. Figure 10-20 Subdivisión del tramo para el tránsito de la onda dinámica. |
In practice, a (mixed) dynamic wave solution represents an order-of-magnitude increase in complexity and associated data requirements when compared to either kinematic or diffusion wave solutions. Its use is recommended in situations where neither kinematic nor diffusion wave solutions are likely to adequately represent the physical phenomena. In particular, (mixed) dynamic wave solutions are applicable to dam-breach flood waves, flow over very flat slopes, flow into large reservoirs, strong backwater conditions and flow reversals. In general, the (mixed) dynamic wave is recommended for cases warranting a precise determination of the unsteady variation of river stages.
En la práctica, una solución de onda dinámica (mixta) representa un incremento de orden de magnitud en la complejidad y requerimientos de los datos asociados cuando se compara con cualquiera de las soluciones de ondas cinemáticas o de difusión. Su uso se recomienda en situaciones donde ni las soluciones de onda cinemática ni de onda de difusión pueden ofrecer una representación adecuada de los fenómenos físicos. En particular, las soluciones de onda dinámica (mixta) son aplicables a las ondas de avenida de la rotura de la presa, flujo sobre las pendientes muy planas, flujo dentro de grandes reservorios, condiciones de remanso fuertes y reversiones de flujo. En general, las onda dinámica (mixta) se recomienda para los casos que justifican una determinación precisa de la variación no permanente de las etapas fluviales.
The current version (Version 4.1) of the U.S. Army Corps of Engineers' HEC-RAS model (U.S. Army Corps of Engineers, 2010) contains a dynamic wave module suited for practical applications.
La versión actual (versión 4.1) del modelo de U.S. Army Corps of Engineers' HEC-RAS (U.S. Army Corps of Engineers, 2010) contiene un módulo de onda dinámica adecuado para aplicaciones prácticas.
Mixed dynamic rating curve / Curva de gasto dinámico mixto
Mixed dynamic wave solutions are often referred to as hydraulic river routing. As such, they have the capability to calculate unsteady discharges and stages when presented with the appropriate geometric channel data and initial and boundary conditions. Their importance in unsteady flow is examined here by comparing them to kinematic and diffusion waves.
Las soluciones de ondas dinámicas mixtas se conocen como tránsito hidráulico del río. Como tales, tienen la capacidad de calcular las descargas y niveles de la superficie del agua no permanentes cuando se presenta con los datos geométricos del canal apropiados y las condiciones iniciales y de contorno. Su importancia dentro del flujo no permanente se examina aquí al comparalas con las ondas cinemáticas y de difusión.
Kinematic waves calculate unsteady discharges; the corresponding stages are subsequently obtained from the appropriate rating curves. Equilibrium (steady, uniform) rating curves are used for this purpose. Diffusion waves may or may not use equilibrium rating curves to calculate stages. Some methods, e.g., Muskingum-Cunge, use equilibrium ratings, but more elaborate diffusion wave solutions may not.
Las ondas cinemáticas calculan descargas no permanentes; las etapas correspondientes son posteriormente obtenidas de las curvas de gasto adecuadas. Las curvas de gasto de equilibrio (uniforme, permanente) se utilizan para este propósito. Las ondas de difusión pueden o no pueden utilizar las curvas de gasto de equilibrio para calcular los niveles de la superficie del agua. Algunos métodos, por ejemplo, de Muskingum-Cunge, utilizan las curvas de gasto de equilibrio, pero las soluciones de onda de difusión más elaboradas no pueden.
Mixed dynamic waves rely on the physics of the phenomena as built into the governing equations to generate their own unsteady flow rating. A looped rating curve is produced at every cross section, as shown in Fig. 10-21. For any given stage, the discharge is higher in the rising limb of the hydrograph and lower in the receding limb. This loop is due to hydrodynamic reasons and should not be confused with other loops, which may be due to erosion, sedimentation, or changes in bed configuration.
Las ondas dinámicas mixtas se basan en la física de los fenómenos inlcuídos dentro de las ecuaciones de gobierno para generar su propia curva en ciclo de flujo no permanente. Una curva de gasto en ciclo se produce en cada sección transversal, como se muestra en la Fig. 10-21. Para cualquier nivel de superficie de agua dada, la descarga es mayor en la rama ascendente del hidrograma y menor en el el lado de descenso. Este ciclo se debe a razones hidrodinámicas y no debe confundirse con otros ciclos, que se deben a la erosión, la sedimentación, o cambios en la configuración del lecho.
Figure 10-21 Sketch of the looped rating of dynamic waves.
Figure 10-21 Esquema de la curva de gasto en ciclo |
The width of the loop is a measure of the flow unsteadiness, with wider loops corresponding to highly unsteady flow. If the loop is narrow, it implies that the flow is mildly unsteady, perhaps a diffusion wave. If the loop is practically nonexistent, the flow can be approximated as kinematic flow. In fact, the basic assumption of kinematic flow is that momentum can be simulated as steady uniform flow, i.e., that the rating curve is single-valued.
La anchura del ciclo es una medida de la inestabilidad del flujo, los ciclos más amplios corresponden a un flujo altamente no permanente. Si el ciclo es estrecho, entonces el flujo es ligeramente no permanente, tal vez es una onda de difusión. Si el ciclo es prácticamente inexistente, el flujo se puede tomar como flujo cinemático. De hecho, la suposición básica del flujo cinemático es que el momento se puede simular como flujo uniforme constante, es decir, que la curva de gasto es de un solo valor.
The preceding observations lead to the conclusion that the importance of mixed dynamic waves is directly related to the flow unsteadiness and the associated loop in the rating curve. For highly unsteady flows such as dam-breach flood waves, it may well be the only way to properly account for the looped rating. For other less unsteady flows, kinematic and diffusion waves are a viable alternative, provided their applicability can be clearly demonstrated.
Las observaciones anteriores llevan a la conclusión de que la importancia de las ondas dinámicas mixtas están directamente relacionada con la inestabilidad de flujo y el ciclo en la curva de gasto. Es posible que en la única instancia en que se puedan explicar adecuadamente las curvas de gasto con ciclos sea en el caso de flujos altamente no permanentes como las ondas de avenidas en la rotura de presas. Para otros flujos no permanentes menores, las ondas cinemáticas y de difusión son una alternativa viables, siempre que se pueda demostrar claramente su aplicación.
Downstream boundary condition / Condición de límite aguas abajo
Modeling of a mixed dynamic wave presents an interesting paradox: In order to solve the problem correctly, a dynamic downstream boundary condition (usually a rating curve) must be specified. However, a dynamic downstream boundary condition is not known a priori. Abbott (1976) put it in the right perspective when he stated:
El modelado de una onda dinámica mixta presenta una paradoja interesante: Para poder resolver el problema correctamente, se debe especificar una condición de frontera aguas dinámica abajo (por lo general una curva de gasto). Sin embargo, se desconoce una condición de frontera dinámica aguas abajo a priori. Abbott (1976) lo puso en una perspectiva correcta cuando dijo:
"A common source of error is the use of a boundary condition in a dynamic model that is really only proper to a pure kinematic model... but in a dynamic model the solution itself generates different discharge-stage relations according to the variabilities of the flows, so that a unique relation at the boundary contradicts the solution within the boundary. A finely balanced model will usually go unstable in this situation, but models with heavy numerical damping may survive, only to give erroneous results."
"Una fuente de error común es el uso de una condición de límite en un modelo dinámico lo cual es realmente adecuado sólo en un modelo cinemático puro ... pero en un modelo dinámico la solución en sí genera diferentes relaciones de descarga-nivel de la superficie del agua de acuerdo a las variabilidades de la flujos, por lo que una relación única en el límite contradice la solución dentro del límite. Un modelo bien balanceado usualmente perderá su balance en esta situació, pero los modelos con amortiguación numérica pesada pueden sobrevivir, pero solamente para dar resultados erróneos. "
A way out of this difficulty is to artificially extend the channel several subreaches downstream, and to specify a kinematic rating at the newly defined downstream boundary, while giving the loop a chance to develop at the upstream cross section of interest (Fig. 10-22). Ponce and Lugo (2001) have used sensitivity analysis to show that the artificial extension of the channel by an amount equal to the channel length (i.e., doubling the channel length) may be sufficient to produce an accurate looped rating at the cross section of interest.
Una manera de salir de esta dificultad es extender aguas abajo artificialmente al canal lo largo de varios subtramos, y de determinar una curva de gasto cinemática en el límite aguas abajo que acaba de definirse, mientras que se le da una oportunidad al ciclo de desarrollarse en la sección transversal aguas arriba de interés (Fig. 10-22 ). Ponce y Lugo (2001) han utilizado análisis de sensibilidad para demostrar que la extensión artificial del canal por una cantidad igual a la longitud del canal (es decir, la duplicación de la longitud del canal) puede ser suficiente para producir una curva de gasto en ciclo precisa en la sección transversal de interés.
Figure 10-22 Artificial extension of the computational domain, for use in mixed dynamic wave
Figure 10-22 Extensión artificial del dominio computacional, para uso en modelos de onda
dinámica |
QUESTIONS / PREGUNTAS
|
|
What conservation laws are used in the description of steady gradually varied flow?
¿Qué leyes de conservación se utilizan en la descripción del flujo permanente gradualmente variado?
What conservation laws are used in the description of unsteady gradually varied flow?
¿Qué leyes de conservación se utilizan en la descripción del flujo no permanente gradualmente variado?
What forces are acting in a control volume in unsteady gradually varied flow?
¿Qué fuerzas actúan sobre un volumen de control en el flujo no permamente gradualmente variado?
What waves types are common in unsteady open-channel flow?
¿Qué tipos de ondas son comunes en el flujo no permanente en canales?
To what problems do kinematic waves apply?
¿A qué tipo de problemas se aplican las ondas cinemáticas?
To what problems do diffusion waves apply?
¿A qué tipo de problemas se aplican las ondas de difusión?
How is Lo defined?
¿Cómo se define Lo?
What is the dimensionless wavenumber?
¿Qué es el número de onda adimensional?
What is the dimensionless relative celerity of kinematic waves under Chezy friction in hydraulically wide channels?
¿Cuál es la celeridad relativa adimensional de las ondas cinemáticas bajo la fricción Chezy en canales hidráulicamente anchos?
What is the dimensionless relative celerity of dynamic waves under Chezy friction in hydraulically wide channels?
¿Cuál es la celeridad relativa adimensional de las ondas dinámicas bajo la fricción Chezy en canales hidráulicamente anchos?
What are three ways of expressing the convective celerity of kinematic waves?
¿Cuáles son las tres formas de expresar la celeridad convectiva de las ondas cinemáticas?
What is the neutral-stability Froude number for triangular channels with Chezy friction?
¿Cuál es el número de Froude de estabilidad neutral para canales triangulares con fricción de Chezy?
What is the neutral-stability Froude number for hydraulically wide channels with Manning friction?
¿Cuál es el número de Froude de estabilidad neutral para los canales hidráulicamente anchos con fricción de Manning?
What is the basis of the Muskingum-Cunge method?
¿Cuál es la base del método de Muskingum-Cunge?
What is Hayami's contribution to flood routing?
¿Cuál es la contribución de Hayami para el tránsito de avenidas?
For what value of Vedernikov number are kinematic and dynamic hydraulic diffusivities the same?
¿Las difusividades hidráulicas cinemáticas y dinámicas son las mismas bajo que número de Vedernikov?
For what value of Vedernikov number does the dynamic hydraulic diffusivity vanish?
¿Bajo qué valor del número de Vedernikov se desaparece la difusividad hidráulica dinámica?
What part of the flood routing does the Muskingum parameter X account for?
¿Qué parte del tránsito de avenidas representa el parámetro de Muskingum X?
What is numerical diffusion?
¿Qué es la difusión numérica?
What is numerical dispersion?
¿Qué es la dispersión numérica?
What is the advantage of the Muskingum-Cunge method?
¿Cuál es la ventaja del método Muskingum-Cunge?
When will the Muskigum-Cunge method fail to give good results?
¿En que situación no dará buenos resultados el método de Muskingum-Cunge?
How is the downstream boundary specified in a mixed kinematic-dynamic model if increased accuracy is desired?
¿Cómo se especifica el límite aguas abajo de un modelo cinemático-dinámico mixto si se desea una mayor precisión?
PROBLEMAS
|
|
You are observing the rise of a river during flood. The width of the river at the observation point, and for some distance upstream is 65 m, and according to the gage reading, the discharge is Q = 70 m3/s. Estimate the discharge at a point located 15.875 km upstream, if the water surface is rising at the rate of 9 mm/hr at your location and at 12 mm/hr at the upstream cross section.
Usted está observando el ascenso de un río durante las avenidas. El ancho del río en el punto de observación, y por alguna distancia aguas arriba es 65 m, y de acuerdo a la lectura del medidor, la descarga es Q = 70 m3/s. Estimar la descarga en un punto situado a 15,875 km aguas arriba, si la superficie del agua está aumentando a un ritmo de 9 mm/hr en su ubicación y en 12 mm/hr en la sección transversal aguas arriba.
A hydraulically wide channel is operating at Froude number F = 0.22. The unit-width discharge is q = 2.8 m2/s. What are the two absolute Lagrange celerities?
Un canal hidráulicamente ancho opera con un número de Froude F = 0.22. La descarga por unidad de ancho es q = 2.8 m2/s. ¿Cuáles son las dos celeridades absolutas de Lagrange?
A flood wave is traveling inbank through a straight river reach of top width T = 320 m wide and length L = 5625 m. For every 1 cm of flood rise, the discharge goes up 10 m3/s. How long will it take for a given discharge to travel the length of the reach?
Una onda de avenida se desplaza dentro del banco a través de un tramo de río recto de ancho de superficie T = 320 m y longitud L = 5,625 m. Por cada 1 cm de aumento de avenida, la descarga sube 10 m3/s. ¿Cuánto tiempo se necesita para que una descarga dada viaje la longitud del tramo?
Calculate the exponent β of the discharge-area rating for a triangular channel with Chezy friction.
Calcular el exponente β de la curva de gasto de la descarga-área para un canal triangular con fricción de Chezy.
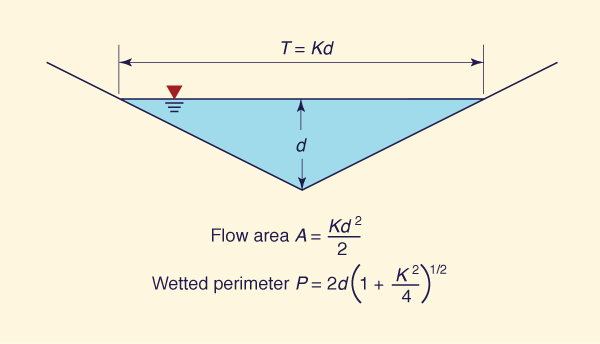
Fig. 10-23 Definition sketch for a triangular channel.
Fig. 10-23 Esquema de definición para un canal triangular.
Calculate the exponent β of the discharge-area rating for a triangular channel with Manning friction.
Calcular el exponente β de la curva de gasto de descarga-área para un canal triangular con fricción de Manning.
A flood hydrograph has the following data: time-of-rise tr = 2 hr, reference velocity Vo = 2 ft/s, reference flow depth do = 6 ft, bottom slope So = 0.004. Determine if this wave is a kinematic wave.
Un hidrograma de avenidas tiene los siguientes datos: tiempo de elevación tr = 2 hr, velocidad de referencia Vo = 2 pies/s, profundidad del flujo de referencia do = 6 pies, pendiente del lecho So = 0.004. Determinar si ésta es una onda cinemática.
A flood hydrograph has the following data: time-of-rise tr = 2 hr, reference velocity Vo = 2 ft/s, reference flow depth do = 6 ft, bottom slope So = 0.004. Determine is this wave is a diffusion wave.
Un hidrograma de avenidas tiene los siguientes datos: tiempo de elevación tr = 2 hr, velocidad de referencia Vo = 2 pies/s, profundidad de flujo de referencia do = 6 pies, pendiente del lecho So = 0.004. Determinar si ésta es una onda de difusión.
A flood hydrograph has the following data: time-of-rise tr = 1 hr, reference velocity Vo = 2 m/s, reference flow depth do = 2 m, bottom slope So = 0.0004. Determine if this wave is a diffusion wave.
Un hidrograma de avenidas tiene los siguientes datos: tiempo de elevación tr = 1 hr, velocidad de referencia Vo = 2 m/s, profundidad de flujo de referencia do = 2 m, pendiente del lecho So = 0.0004. Determinar si ésta es una onda de difusión.
Using ONLINE ROUTING 04, route a flood wave using the Muskingum method. The inflow hydrograph ordinates are [25 ordinates, starting at time = 0, to time = 24 hr]:
100, 130, 150, 180, 220, 250, 300, 360, 450, 550, 700, 550, 490, 370, 330, 310, 280, 230, 170, 150, 130, 120, 110, 105, 100.
Assume Δt = 1 hr, K = 1 hr, X = 0.3. Report the peak outflow and time of occurrence.
Usando ONLINE ROUTING 04, transite una onda de avenidas usando el método de Muskingum. Las ordenadas del hidrograma del flujo de entrada son [25 ordenadas, comenzando en el tiempo = 0, al tiempo = 24 hr]:
100, 130, 150, 180, 220, 250, 300, 360, 450, 550, 700, 550, 490, 370, 330, 310, 280, 230, 170, 150, 130, 120, 110, 105, 100.
Asumir Δt = 1 hr, K = 1 hr, X = 0.3. Reportar el flujo de salida pico y el tiempo en el que ocurre.
Using ONLINE ROUTING 05, route the same flood wave as the previous problem using the Muskingum-Cunge method. Use the following input data: Qp = 700 m3/s, Ap = 400 m2,
Tp = 88 m, Δt = 1 hr, Δx = 9.6 km, β = 1.65, So = 0.0007. Report the peak outflow and time of occurrence.Usando ONLINE ROUTING 05, transite la misma onda de avenida descrito en el problema anterior utilizando el método de Muskingum-Cunge. Utilizar los siguientes datos de entrada:
Qp = 700 m3/s, Ap = 400 m2,Tp = 88 m, Δt = 1 hr, Δx = 9.6 km, β = 1.65, So = 0.0007. Reportar el flujo de salida pico y el tiempo en el que ocurre.
BIBLIOGRAFÍA
|
|
Abbott, M. A. 1976. Computational hydraulics: A short pathology. Journal of Hydraulic Research, Vol. 14, No. 4, p. 276.
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York.
Craya, A. 1952. The criterion for the possibility of roll-wave formation. Gravity Waves, Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.
Cunge, J. A. (1969). On the Subject of a Flood Propagation Computation Method (Muskingum Method), Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
Dooge, J . C. I. 1973. Linear theory of hydrologic systems. Technical Bulletin No. 1468, U.S. Department of Agriculture, Washington, D.C.
Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, Diciembre.
Kibler, D. F., y D. A. Woolhiser. 1970. The kinematic cascade as a hydrologic model. Hydrology Paper No. 39, Colorado State University, Ft. Collins, Colorado.
Kleitz, M. 1877. Note sur la théorie du mouvement non permanent des liquides et sur application à la propagation des crues des rivières, (Note on the theory of unsteady flow of liquids and on application to flood propagation in rivers), Annals des Ponts et Chaussées, ser. 5, Vol. 16, 2e semestre, 133-196.
Liggett, J. A. 1975. Basic equations of unsteady flow. Chapter 2 in Unsteady flow in open channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Ft. Collins, Colorado.
Liggett, J. A., y J. A. Cunge. 1975. Numerical methods of solution of the unsteady flow equations. Chapter 4 In Unsteady flow in open channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Ft. Collins, Colorado.
Lighthill, M. J., y G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
McCarthy, G. T. (1938). "The Unit Hydrograph and Flood Routing," unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, 24 de Junio.
Ponce, V, M., y D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, Diciembre, 1461-1476.
Ponce, V. M., y V. Yevjevich. 1978. Muskingum-Cunge method with variable parameters. Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, Diciembre, 1663-1667.
Ponce, V. M., y F. D. Theurer. 1982. Accuracy criteria in diffusion routing. Journal of the Hydraulics Division, ASCE, Vol. 108, No. HY6, Junio, 747-757.
Ponce, V, M., y D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 4, Abril, 600-611.
Ponce, V. M. 1989. Engineering hydrology: Principles and practices. Prentice Hall, Englewood Cliffs, Nueva Jersey.
Ponce, V. M. 1990. Generalized diffusion wave equation with inertial effects. Water Resources Research, Vol. 26, No. 5, Mayo, 1099-1101.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, Julio.
Ponce, V, M., y P. J. Porras. 1995. Effect of cross-sectional shape of free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, Abril, 376-380.
Ponce, V, M., y A. Lugo. 2001. Modeling looped ratings in Muskingum-Cunge routing. Journal of Hydrologic Engineering, ASCE, Vol. 6, No. 2, Marzo-Abril, 119-124.
Saint-Venant, B. de. 1871. Theorie du mouvement non-permanent des eaux avec application aux crues des rivieres et l' introduction des varees dans leur lit, Competes Rendus Hebdomadaires des Seances de l'Academie des Science, París, Francia, Vol. 73, 1871, 148-154.
Seddon, J. A. 1900. River hydraulics. Transactions, ASCE, Vol. XLIII, 179-243, Junio.
U.S. Army Corps of Engineers. 2010. River Analysis System: HEC-RAS, Version 4.1, Hydrologic Engineering Center, Davis, California.
| http://openchannelhydraulics.sdsu.edu |
|
150903 23:10 |