Fig. 1  Professor Victor M. Ponce (2013).


THE MOCKUS INTERVIEW RETOLD


Victor M. Ponce

Professor Emeritus of Civil and Environmental Engineering

San Diego State University, San Diego, California


February 2, 2026

ABSTRACT.  The present article

PRELUDE

In the winter of 1993, the Late Pete Hawkins and I met in Denver while we were both lecturing at an Army Corps of Engineers' Technical Conference. I had known Pete for a few years and was very familiar with his work. It did not escape my attention that he had a good track record on curve number hydrology. At that time, I had completed 13 years of teaching at San Diego State University, and enjoyed a respectable record in hydrology, having recently completed a textbook entitled "Engineering Hydrology, Principles and Practices" (1989). In Denver, over coffee with Pete, I suggested to him that we should team up to write a review paper on the curve number methodology. To my delight, Pete graciously accepted. We planned to coalesce his substantial experience with the curve number with my demonstrated ability to communicate technical concepts in a clear and forthright manner. From the outset, it promised to be a winning association.

Over the next two years, we toiled to complete the paper that we had set out to write. Pete proved to be a meticulous coauthor; to this date, my memory of the experience still resonates positively in my mind. Pete needed to be convinced of my thoughts on the subject; conversely, I may add, I needed to be convinced of his. Being both well seasoned technical writers, we did not shy away from the experience. We completed the manuscript and submitted it for publication in ASCE's newly minted Journal of Hydrologic Engineering. The paper, entitled "Runoff curve number: Has it reached maturity," by Victor M. Ponce and Richard H. Hawkins saw the light of day in the maiden issue of the journal, Vol. 1, No. 1, dated January 1996.

As planned, the paper went through the customary steps for journal publication. There were three discussions, to be duly followed by the authors' closure. As we prepared to write the closure, I had a strong feeling that to do proper justice to the methodology, we needed to get in touch with Victor Mockus. Mockus, a Soil Conservation Service engineer of the 1940's, was widely recognized as a principal author of the methodology. [In 1994, SCS became the Natural Resource Conservation Service, subsequently to be referred to as NRCS]. The original release of the methodology had been dated as 1954. Vic had retired in the 1960's, after an illustrious career in government service, and ostensibly had been out of touch with SCS since then.

PREPARATION

I contacted Don E. Woodward, who at the time (1996) was National Hydraulic Engineer at NRCS, for help in reaching Mockus. Don encouraged me to do it, but cautioned that it could be a slippery road, since about three decades had elapsed and he (Don) understood that Mockus had not been in touch with SCS since his retirement in the 1960's. I have always enjoyed a challenge. At the time I felt that if I was successful in convincing Vic to briefly step out of his self-imposed isolation, that our work would benefit inmensely; to say nothing of the benefit to acrue to the profession at-large.

In July of 1996, I spent a few days in Washington, D.C., purposely to interview Mockus. It did not take me too long to find a working number for him. On the afternoon of July 11, I dialed Vic's number and, to my amazement, Vic himself answered the phone. From there on, I was on my own. The task at hand was to somehow convince Mockus to talk to me about his creation. I knew what I had to do. I had to paint myself as a visitor from afar, clearly not a threat to anybody living near the capital beltway. Therefore, I introduced myself as an academic from California, explaining that I had recently written an ASCE journal paper expounding on Mockus' curve number methodology. I mentioned to Vic that in the paper's closure, at that time in preparation, it was my intention to further clarify, for the benefit of the profession, some of the more important concepts that had underpinned the development of his methodology. To my amazement, Vic responded in a calm fashion: "You can come tomorrow at 3 pm."

TOPICS FOR DISCUSSION

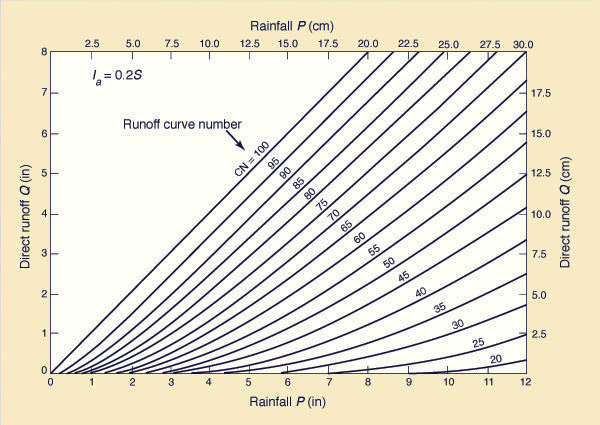
That evening, I prepared myself dutifully for the interview, which was to take place the following day, on July 12. I chose four topics to focus on, very mindful that time was of the essence. These were: (1) The basis of the Mockus' runoff equation, which was, at the time (1996), being used throughout the world, apparently with little second thought; (2) The rationale for the choice of initial abstraction ratio, fixed from the beginning (1954) at λ = 0.2 for general use; (3) The method's suitability for use across biomes, i.e., forests, pasture lands, agricultural lands, and urban landscapes; and (4) The upper limit of watershed size for the applicability of the runoff curve number equation.

THE MOCKUS RUNOFF EQUATION

The overriding question in my mind, and presumably that of countless users of the curve number method, was the origin of the so-called Mockus runoff equation. In other words, how did Vic come up with Eq. 3, as shown in Page 13 of Ponce and Hawkins (1996)? Mockus had plotted direct runoff Q vs rainfall P in inches (Fig. 1), and had proceeded to fit an algebraic equation (Eq. 3) to the data, essentially amounting to a nonlinear fit. While the method had been developed for events, he stated that it had been based on daily data, because that was the only data available in large quantities.

Mockus proceeded with a calmness that revealed that it was not the first time that he had been asked that question. He stated that he had zeroed in on that equation, "One evening, after dinner, seeing that it fitted the data very well, and after having tried many other alternative relations" (NRCS: Miguel Ponce conversation with Vic Mockus).

At this juncture, it is important to mention that Mockus' equation unmistakingly states a complete opposite truth to that of the classical Horton infiltration equation, which preceded Mockus' work by more than two decades (Horton, 1933). Indeed, while Mockus' equation states that retention and runoff are directly related, Horton's equation states no such thing. [It is surmised here that the recognition of this fact may have been the source of many spirited arguments amongst scientists in the early days of infiltration modeling]. Herein lies the essence of the difference between these two historic approaches to infiltration modeling, underscoring the intrinsic value and, therefore, demonstrated permanence of Mockus' approach, vis-à-vis that of Horton's.

Fig. 1  The NRCS runoff curve number equation in graphical form.

INITIAL ABSTRACTION

The initial abstraction Ia was defined as the rainfall amount which took place before the start of runoff, defined as Ia = λ S, in which λ = initial abstraction ratio, and S = potential maximum retention (of the site under study). Mockus confided to me that the choice of initial abstraction ratio had been a decided challenge from the start. In an attempt to circumvent the problem altogether, he preferred to use the quantity (P - Ia) in the abscissas (see Fig. 1), but was overruled by his superiors. They eventually settled on λ = 0.2 because this value appeared to be at the center of the data, although showing quite a scatter.

The value λ = 0.2 has been used in the U.S. and most other countries since its inception in 1954. However, Mockus was of the opinion that if the data warranted, the value could be changed to reflect local field conditions. Extensive curve number experience, particularly in the U.S. and other countries, appears to point in that direction (Ponce and Hawkins, 1996: Page 14). Recently, beginning around the year 2000, Hawkins led a movement in the U.S. to revise and eventually change the value of λ to the smaller value λ = 0.05. (Hawkins et al, 2009). This situation gives some credence to the original Mockus' concern that the chosen value of λ = 0.2 in 1954 for general applications may have been on the high side. NRCS is currently examining the pros and cons of a protracted change of λ from 0.2 to 0.05; to date (2026), no final decision has been forthcoming.

APPLICABILITY ACROSS BIOMES

It was Mockus and his associates who gave the method the name "runoff curve number," and this name was readily accepted for usage throughout the world. Yet the method's paternity is recognized as SCS's, which, four decades later, in 1994, became NRCS. Thus, the method's original scope has been clearly defined from the start: Hydrologic modeling, with the objective of supporting flood and erosion control studies and associated projects, in small agricultural watersheds. In the interview, Mockus noted that the field data used to underpin the method's development had varied in scale from 0.1 to 10 square miles. This fact all but reduces the method's applicability to direct runoff, as opposed to total runoff, which does include baseflow. The latter is typically present in basins larger than 10 square miles, and definitely the case of much larger basins.

It is now widely recognized that the method's best performance is for agricultural watersheds, for which it was originally developed. Its applicability has since been extended to urban sites. The method rates fairly in applications to range sites, and generally does poorly in applications to forest sites (Hawkins 1984; 1993; Ponce and Hawkins, 1996: Page 16).

LIMIT TO WATERSHED SIZE

The comments of the previous paragraph take on a life of their own when it is realized that, over the years, the method's apparent simplicity led to its wide popularity, which encouraged many practitioners to apply the method beyond its original scope, that is, for larger watersheds, which were not necessarily of agricultural type. Mockus himself, when questioned on the practical upper limit to watershed/basin size for use of the curve number methodology, mentioned the 400-square mile limit, in reference to the upper limit for midsize watershed/basin runoff analysis (Ponce, 2014). It should not escape our attention that SCS, and later NRCS, had no clear mandate to perform hydrologic studies in large basins.

CURRENT MODELING PRACTICE

The NRCS runoff curve number method is now widely understood for what it is: A rainfall-runoff model with a definite conceptual basis, amply supported by field data and officially endorsed by a major federal government agency. As Mockus stated in the 1996 interview, he saw no limit to a basin-scale application of the runoff curve number equation, other than that which is imposed by spatial rainfall uniformity. This latter point is crucial to the correct application of the method. As the watershed/basin size increases, the likelihood of spatial rainfall uniformity decreases accordingly, thus, defeating the basic assumption of the methodology. In practice, the 10-square mile limit, as stated by Mockus himself when clarifying the source of the field data, may be widely recognized as a practical upper limit.

Despite more than two decades of intensive research, the resolution of the λ argument (Section 5 above) still awaits an official decision by NRCS (2026). A clear answer to this question remains elusive. A change in λ from the current 0.2 value to a possible future value of 0.05 will trigger a complete change in table runoff curve numbers, with the perceived reluctance to change of a long-established practice. The real issue is whether the new λ will result in an increase in overall accuracy, given the intrinsic lack of precision of the rainfall-runoff problem and the practical impossibility of accurately pinning down the variability; recall the demonstrated sensitivity in calculated peak discharges with a choice of AMC. Only time will tell if the path chosen turns out to be the right one.

DEDICATION

This paper is dedicated to the memory of Richard H. "Pete" Hawkins, Late Professor Emeritus of Civil Engineering, University of Arizona. The writer has had the good fortune of meeting Pete in numerous occasions over the course of their respective careers. In 1996, they teamed up to complete a review paper on curve number hydrology for the ASCE Journal of Hydrologic Engineering. Three decades having now elapsed, in retrospect, their association must have been a very good one, because their 1996 paper coauthorship eventually became, and continues to be the most cited paper on Ponce's Google Scholar site, featuring 1613 citations as of February 2, 2026.

REFERENCES

Hawkins, R. H., T. J. Ward, D. E. Woodward, and J. A. Van Mullem. 2009. Curve Number Hydrology: State of the Practice. Report of ASCE/EWRI Curve Number Hydrology Task Committee, 106 p.

Hawkins, R. H., 1984. A comparison of predicted and observed runoff curve numbers. Proceedings, Specialty Conference, Irrigation and Drainage Division, ASCE, 702-709.

Hawkins, R. H., 1993. Asymptotic determination of runoff curve numbers from data. Journal of the Irrigation and Drainage Division, ASCE, 119(2), 334-345.

Horton, R. E. 1933. The Role of Infiltration in the Hydrologic Cycle. Transactions, American Geophysical Union, Vol. 14, 446-460.

Ponce, V. M., and R. H. Hawkins. 1996. Runoff Curve Number: Has It Reached Maturity? Journal of Hydrologic Engineering, Vol. 1, No. 1, January.

Ponce, V. M. 2014. Engineering Hydrology: Principles and Practices, Prentice-Hall, Englewood Cliffs, New Jersey, Second edition, online, 2014.

260202