♦ Esta página se visualiza mejor con Mozilla Firefox ♦ Fig. 1   Cabecera de la cuenca del río Moyán/La Leche, cerca de Incahuasi, Lambayeque, Perú. PROYECTO DE CONTROL DE INUNDACIONES EN EL RÍO LA LECHE LAMBAYEQUE, PERÚ SEGUNDO INFORME RESULTADOS PRELIMINARES 13 de mayo del 2008 Dr. Victor M. Ponce Consultor en Hidrología 1.   INTRODUCCIÓN D'León Ingenieros Consultores, de Long Beach, California, EE.UU.A., denominado en lo sucesivo DLCE, tiene un contrato con el Gobierno Regional de Lambayeque, Perú, en lo sucesivo, GRL, para apoyar el desarrollo del proyecto de control de inundaciones del río La Leche. 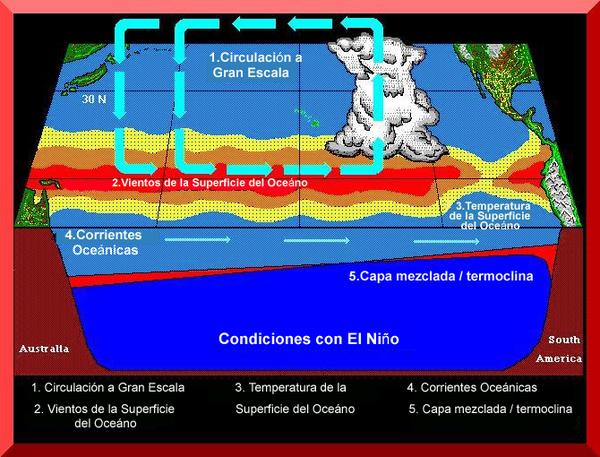El estudio tiene por objeto el control de las inundaciones y la conservación del agua en la cuenca del río La Leche, que ha sufrido graves inundaciones causadas por el fenómeno de El Niño (Fig. 2). Fig. 2   El fenómeno de El Niño (Fuente: UC Santa Barbara). El organismo de financiación es la Agencia de Desarrollo y Comercio de los EE.UU. (UST&DA). La entidad del gobierno local a cargo del proyecto es el Proyecto Especial Olmos-Tinajones, en lo sucesivo PEOT. Dr. Víctor M. Ponce, en lo sucesivo el Consultor, tiene un subcontrato con DLCE para llevar a cabo el componente hidrológico del estudio. Este segundo informe se presenta en cumplimiento parcial de los requisitos del contrato entre el Consultor y DLCE. El informe contiene una descripción de los avances realizados a la fecha y un resumen de las conclusiones preliminares. 2.   DESCRIPCIÓN DEL PROYECTO El proyecto abarca el diseño de factibilidad de la estructura [o estructuras] para controlar las inundaciones en la cuenca del río La Leche y almacenar las aguas para su uso posterior. Actualmente, se están considerando dos sitios de presa: (1) La Calzada, y (2) Calicantro (DEPOLTI, 1998). La presa La Calzada está localizada encima de la corriente principal, mientras que Calicantro está fuera de la corriente principal. El Cuadro 1 muestra una comparación entre estas dos alternativas. Cuadro 1.   Comparación entre las alternativas de presa. 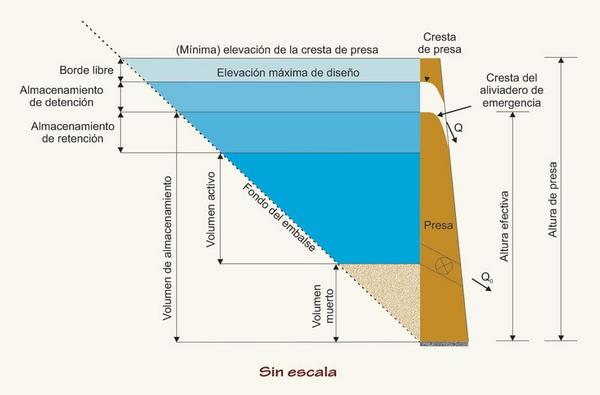Capacidad Alternativa de sitio de presa La Calzada Calicantro La Calzada y Calicantro Control de inundación Muy bueno Ineficiente Muy bueno Almacenamiento de agua Regular Muy bueno Muy bueno Vida útil del reservorio Corta Larga Larga Si se construye la presa sólo en La Calzada, servirá muy bien para controlar las inundaciones. Sin embargo, la eficacia del control dependerá de qué porcentaje del almacenamiento activo se reserva para el almacenamiento de retención de la avenida (Fig. 9). Por lo tanto, una sola presa en La Calzada no será eficaz para el almacenamiento de aguas para uso posterior. Además, una presa grande dentro de la corriente, como La Calzada, tendría una tendencia a almacenar grandes cantidades de sedimentos, limitando la vida útil del reservorio (estimaciones preliminares indican que podría ser menor de 100 años). Si se construye una presa sólo en Calicantro, ésta podrá almacenar grandes cantidades de agua. Sin embargo, no servirá para atenuar eficazmente las grandes inundaciones del río La Leche. Estando fuera de la corriente principal, la presa en Calicantro no estará sujeta al riesgo de deposición de grandes cantidades de sedimentos, lo que aumentará la vida útil del reservorio. Esto último se aplica siempre y cuando haya una buena obra de exclusión [desarenador] en el lugar, y que ésta sea operada correctamente. La solución es construir dos presas, una en La Calzada, principalmente para el control de inundaciones, y otra en Calicantro, para almacenar agua para el riego y otros usos. Con la estrategia de dos represas, la vida útil aumentará, especialmente la de La Calzada. El agua no permanecerá demasiado tiempo en La Calzada, y se podría desarenar antes de enviarla a Calicantro para su almacenamiento. La presa de La Calzada exige una minuciosa evaluación de la hidrología de inundaciones, ya que se trata de una presa relativamente grande situada aguas arriba de importantes centros poblados. La presa de Calicantro tiene una pequeña área de drenaje, por lo que las inundaciones regionales no deberán ser un problema, garantizando la seguridad de la presa contra el rebasamiento. Sin embargo, el vertedero tendrá que ser diseñado apropriadamente, y su capacidad calculada. El enfoque del presente estudio es la modelación de precipitación-escorrentía en toda la cuenca del río La Leche, desde su cabecera hasta el sitio de presa en La Calzada. Esto permite el cálculo de los hidrogramas para determinar la capacidad del aliviadero principal y del (los) aliviadero(s) de emergencia, y la elevación mínima de la coronación de la presa. Para La Calzada se determinan los hidrogramas para el aliviadero principal (HAP), aliviadero de emergencia (HAE), y el hidrograma del borde libre (HBL). También se determinan hidrogramas de diseño para la presa de Calicantro. 3.  DESCRIPCIÓN DE LA CUENCA La cuenca del río La Leche, desde su cabecera hasta La Calzada, tiene un área de drenaje de 907.36 km2. La cuenca está ubicada en las laderas occidentales de los Andes Occidentales Peruanos. La población más grande dentro de la cuenca es Incahuasi, con cerca de 15,000 habitantes, incluída la población rural. La distancia a Chiclayo, la ciudad más cercana, es de 120 km. El tiempo de viaje a lo largo de una carretera afirmada es de aproximadamente 6 horas. En temporada de lluvias, los viajes hacia y desde Incahuasi pueden ser peligrosos y sujetos a demora. La cabecera de la cuenca del río La Leche está localizada en el Cerro Choicopico, a una altitud de 4,230 m sobre el nivel medio del mar. El río La Leche tiene dos afluentes principales: el Moyán y el Sangana. La longitud hidráulica del río La Leche, a La Calzada, a lo largo del Moyán, es de 44,397 m. La longitud hidráulica a lo largo del Sangana es de 44,591 m. La pendiente de los canales varía desde 24% en la Quebrada Cascabamba hasta 1% cerca a La Calzada. La velocidad media durante las inundaciones varía entre 3 y 4 m/s. El tiempo de concentración varía de 3 a 4 hr. El uso de la tierra es mixto, con presencia de bosques, praderas, y tierras de cultivo. Las pendientes medias del terreno son relativamente altas, variando del 20% al 50%, lo cual fomenta la escorrentía superficial. Las laderas muy empinadas tienen roca expuesta y muy poco suelo, lo que limita la infiltración (Fig. 3). La precipitación varía espacialmente dentro de la cuenca en función de la altitud. Las tormentas son más fuertes e intensas por debajo de los 1500 m de altura (hacia el oeste), y menos fuertes por encima de los 1500 m (hacia el este). El clima es semiárido hacia el oeste, cambiando gradualmente a subhúmedo hacia el este. Existen tres estaciones climatológicas dentro de la cuenca del río La Leche: (1) Puchaca (2), Tocmoche, e (3) Incahuasi. El Cuadro 2 muestra una comparación entre estas estaciones. La estación Puchaca está a 500 m de altitud; la estación Tocmoche a 1,380 m, y la estación Incahuasi a 2,740 m. El mes más húmedo en Puchaca es diciembre; contrariamente, el mes más húmedo en Tocmoche e Incahuasi es marzo. Puchaca tiene menor precipitación anual, pero las tormentas son más fuertes. Incahuasi tiene mayor precipitación anual, pero las tormenta son más leves. Tocmoche tiene precipitación anual e intensidad de tormenta intermedia entre las de Puchaca e Incahuasi. Fig. 3   Afloramientos rocosos en terrenos agrícolas en cuestas empinadas de la cuenca del río La Leche. Cuadro 2.   Comparación entre las estaciones climatológicas en la cuenca del río La Leche. Característica Estación Puchaca Tocmoche Incahuasi Localización parte baja centro cabecera Elevación (m) 500 1,380 2,740 Latitud 6o 21' S 6o 24' S 6o 14' S Longitud 79o 28' W 79o 21' W 79o 20' W Longitud del registro 1963-2002 1964-2007 1963-2007 Mes más húmedo diciembre marzo marzo Precipitación anual baja media alta Intensidad de tormenta alta media baja La tormenta máxima de 24 horas en Puchaca es 150.2 mm; en Tocmoche es 110 mm; y en Incahuasi, 81 mm. La tormentas son más intensas cerca a Puchaca y menos intensas en la vecindad de Incahuasi, con Tocmoche en el medio. 4.   ESTRATEGIA DE MODELACIÓN Existe la necesidad de determinar las descargas pico asociadas con períodos de retorno de 100 años a 10,000 años. La única estación de aforos, en Puchaca, tiene registros desde 1956 (Fig. 4). La máxima descarga registrada en Puchaca es 579.75 m3/s. La evidencia geomorfológica sugiere que a largo plazo los flujos de avenida en La Calzada pueden haber superado este valor. La enorme llanura aluvial del río La Leche no podría haber sido formada en ausencia de grandes inundaciones. Para fines de diseño, cuando el período de retorno (en este caso, 10,000 años) supera en extremo a la longitud del registro (cerca de 50 años), se recomienda que el análisis se base en la transformación precipitación-escorrentía. Esta última pone mayor enfásis en la precipitación, la cual tiene usualmente más datos y está sujeta a menos variabilidad. Además, la modelación de precipitación-escorrentía es capaz de examinar situaciones hipotéticas tanto en lo que respecta al tipo de tormenta (en tamaño e intensidad), como a los diversos tipos de complejo suelo/cobertura, naturales y artificiales. En el caso de la cuenca del río La Leche, se espera que la avenida de diseño se produzca bajo una combinación apropiada de los siguientes factores: Profundidad de lluvia:   Aplicable al fenómeno de El Niño, el cual ocurre cada 12 a 15 años en promedio; Cobertura de lluvia:  Una tormenta general, que cubre todo el área de la cuenca; y Secuencia de tormentas:  Una tormenta intensa que ocurre poco después de otra tormenta intensa, resultando en una condición antecedente húmeda. La estrategia elegida es la modelación de la cuenca del río La Leche utilizando el modelo RAINFLO©, el cual es un modelo determinístico/conceptual de precipitación-escorrentía. Las tormentas de 24 horas, de 100 años y 10,000 años de período de retorno, se calculan utilizando los métodos de Log Pearson III y Gumbel. Estos datos de tormenta alimentan al modelo, el cual calcula los caudales de avenida para los diferentes períodos de retorno seleccionados. 5.   DESCRIPCIÓN DEL MODELO RAINFLO© es un modelo computacional de precipitación- escorrentía, determinístico/ conceptual, distribuído, de evento, desarrollado específicamente para el cálculo de flujos de avenida (Ponce et al., 1985). El modelo calcula hidrogramas de avenida cuando se le presenta con las precipitaciones adecuadas, las características fisiográficas de la cuenca, y las características del suelo y uso de la tierra. El modelo es determinístico porque el tránsito de avenidas se calcula con el método Muskingum-Cunge, el cual simula la onda difusiva (Ponce y Simons, 1977; Ponce y Yevjevich, 1979). En este método, el tiempo de translación K está basado en la ley de Seddon (Seddon, 1900). Además, el factor de ponderación X se basa en la difusividad hidráulica de Hayami y en el coeficiente de difusión numérica de Cunge (Hayami, 1951; Cunge, 1969). Esta metodología ofrece las siguientes ventajas: Los parámetros de tránsito de avenidas se basan en propiedades hidráulicas de la cuenca, incluyendo la descarga por unidad de ancho, la pendiente del canal, y las características [forma] de la sección transversal, en vez de mediciones hidrológicas de aforos, y El cálculo es independiente de la malla elegida, dentro de límites apropiados. La primera ventaja permite tránsitos de avenida precisos, aun cuando los arroyos o ríos no hayan sido aforados, y para todo el rango posibles de flujos, desde los más bajos hasta los más altos. La segunda ventaja implica que el cálculo es consistente con las ecuaciones diferenciales que gobiernan el proceso físico, pues el mismo resultado es obtenido en varias corridas, independientemente del tamaño de malla especificada. El modelo es conceptual porque la abstracción hidrológica se calcula con el método del número de la curva, el cual simula conceptualmente el llenado del reservorio del suelo (Ponce, 1996). A diferencia del enfoque clásico de Horton, en el cual es posible la infiltración infinita [en el tiempo], en el método del número de la curva la profundidad del infiltración alcanza asimptóticamente un valor constante (el potencial máximo de retención S) conforme la tormenta aumenta de tamaño (Horton, 1933; Servicio de Conservación de Recursos Naturales, 1985b). La experiencia con el método del número de la curva indica que es el más adecuado para modelar la infiltración bajo condiciones de evento [tormenta]. Su amplia aplicabilidad se atribuye a su base conceptual, aunque es necesario ejercer un cuidado razonable para utilizar el método en forma apropiada. El modelo es distribuído porque es capaz de calcular los flujos de avenida, conforme varían en el espacio y en el tiempo, en cualquier punto de la red donde una subcuenca de cabecera colecta su drenaje, o donde dos subcuencas de tramo se reúnen (Fig. 5). El número de lugares donde los resultados pueden ser obtenidos depende del grado de subdivisión de la cuenca. El valor típico para el número de subcuencas varía entre 10 y 100, y los requerimientos de datos aumentan conforme aumenta el número de subcuencas (Ponce et al., 1985; Ponce et al., 2005). Fig. 4  Estación de aforos, río La Leche en Puchaca. Fig. 5   Cerro Lajas de Tongon, cerca a la confluencia de los ríos Moyán y Sangana, cuenca La Leche. El modelo es de evento porque simula los flujos de avenida en situaciones en las que la escorrentía directa constituye la mayor parte del flujo, es decir, cuando el flujo de base es pequeño y no contribuye apreciablemente al pico de la avenida. A diferencia de la modelación contínua, los modelos de evento no requieren una contabilidad de la humedad a largo plazo. De este modo, los resultados de simulaciones de evento son consecuentes con variaciones típicas en los parámetros. Por otra parte, la estructura topológica única del modelo le permite considerar una cuenca dendrítica de cualquier orden. Los hidrogramas de avenida son calculados y expresados en cualquier punto de confluencia de la red hidrográfica. El modelo es de precipitación-escorrentía porque busca, a través de una transformación adecuada, convertir lluvia efectiva (mm) en escorrentía (m3/s). La transformación se realiza a través de la convolución del hidrograma unitario con la tormenta efectiva, obteniéndose así el hidrograma de avenida para cada subcuenca (Servicio de Conservación de Recursos Naturales, 1985b). La aplicabilidad del hidrograma unitario para cuencas de tamaño medio, es decir, aquéllas con áreas de drenaje de 1 a 1000 km2 [como las del río La Leche], ha sido apliamente documentada (Ponce, 1989). El modelo es computacional porque discretiza las ecuaciones de conservación de la masa y cantidad de movimiento (expresadas en la onda cinemática) en el espacio y en el tiempo, mediante el uso de un esquema numérico apropiado (Ponce, 1989). Sin embargo, este último está sujeto a ciertas condiciones de estabilidad y convergencia. La estabilidad se refiere a la abilidad del esquema para marchar en el tiempo evitando el crecimiento ilimitado de errores. La convergencia se refiere a la abilidad del esquema para reproducir los términos de la ecuación diferencial con suficiente precisión. Las ecuaciones diferenciales se expresan en diferencias finitas, utilizando los intervalos de espacio y tiempo, Delta x y Delta t, respectivamente. Las propiedades numéricas del modelo dependen de la correcta elección de la resolución espacial y temporal, es decir, del número de Courant (Ponce, 1989). Como tal, este último controla, no sólo la estabilidad, sino también la convergencia de esquemas numéricos de sistemas hiperbólicos de ecuaciones diferenciales parciales. En resumen, el modelo RAINFLO© involucra más de cincuenta años de investigación en procesos hidrológicos, entre ellos la abstracción (con el número de la curva), la transformación precipitación-escorrentía (con el hidrograma unitario), y el tránsito de avenidas (con el método Muskingum-Cunge). La combinación de métodos determinísticos y conceptuales de los procesos hidrológicos relevantes hacen especialmente atractivo al modelo. 6.   RECOPILACIÓN DE DATOS Los datos requeridos son los siguientes: Topología de la cuenca Propriedades geométricas de las subcuencas Pendientes medias del terreno Lluvias de evento Grupos hidrológicos de suelo Coeficientes de Manning Secciones transversales 6.1   Topología de la cuenca La cuenca de La Leche, desde su cabecera hasta La Calzada, se divide en nueve (9) subcuencas de cabecera y diecisiete (17) subcuencas de tramo, haciendo un total de veintiséis (26) subcuencas (Fig. 6). La escorrentía en cada subcuenca puede ser local o importada. La escorrentía local se origina dentro de cada subcuenca y se calcula por convolución del hidrograma unitario con la precipitación efectiva. La escorrentía importada se origina aguas arriba de una subcuenca de tramo y se transita utilizando el método Muskingum-Cunge. Las subcuencas de cabecera están numeradas consecutivamente (del 1 al 9), en el orden de número creciente de la subcuenca de tramo adyacente. Las subcuencas de tramo están numeradas, de aguas arriba hacia aguas abajo, utilizando un número topológico de cinco dígitos, que indica el orden-ramal-tramo (Fig. 6). 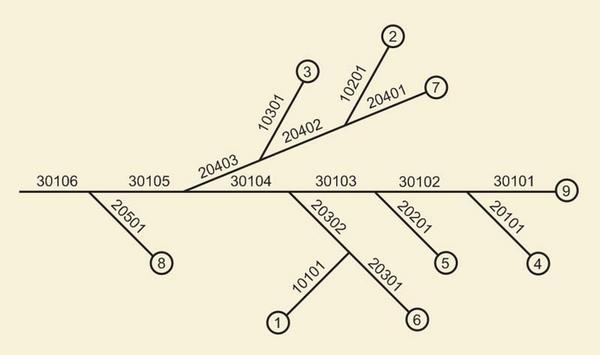Fig. 6   Topología de la cuenca La Leche. 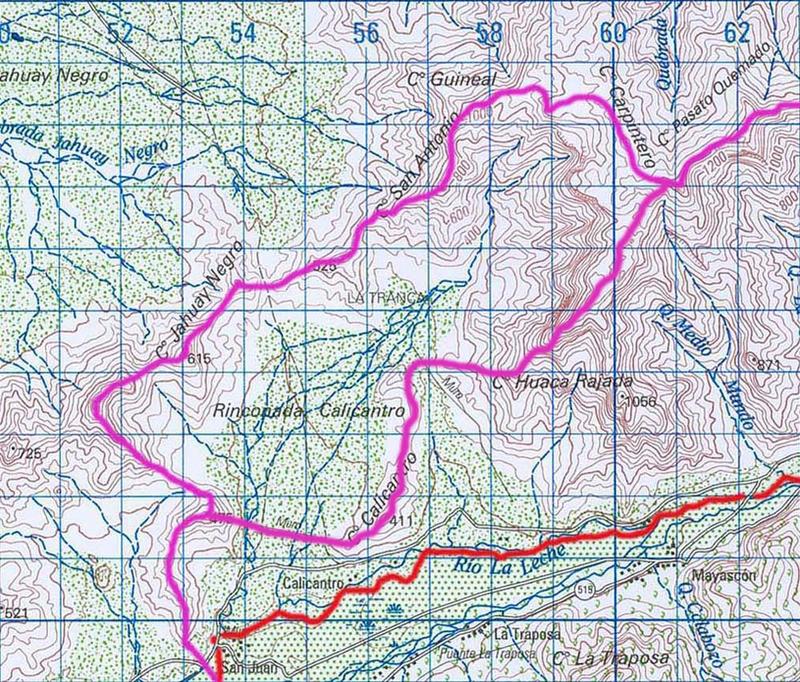6.2   Propiedades geométricas de la subcuencas Las propiedades geométricas de las subcuencas se obtienen a partir de mapas topográficos a escala 1:100,000 (cartas IGN Incahuasi y Jayanca). La delimitación de las subcuencas se muestra en la Fig. 7. Esta figura incluye el área de drenaje del río La Leche hasta un punto localizado aguas abajo del sitio Calicantro (Fig. 14). Las características geográficas se muestran en el Cuadro 3. Las áreas de drenaje se delimitan siguiendo los picos y las monturas de la topografía. Las longitudes hidráulicas y las pendientes de los canales se obtienen de los mapas. Las propiedades hidrológicas se muestran en el Cuadro 4. En este cuadro, la última subcuenca de tramo (30106) incluye las propiedades hidrológicas sólo hasta La Calzada. Las áreas de drenaje varían entre un mínimo de 708 ha (Quebrada del Verde) y un máximo de 8,815 ha (río Moyán 3), con un promedio de 3,490 hectáreas. El total de área de drenaje para el río La Leche a La Calzada es 90,736 ha, o 907.36 km2. La longitud hidráulica del río Moyán / La Leche, desde la cabecera al sitio de presa propuesto es 44,397 m. La longitud hidráulica del río Sangana / La Leche es 44,591 m. La pendiente media de los tramos de canales varía entre un máximo de 0.24 para la Quebrada Cascabamba (subcuenca de cabecera 6), y un mínimo de 0.01 para el río La Leche 2, inmediatamente aguas arriba de La Calzada (subcuenca de tramo 30106). 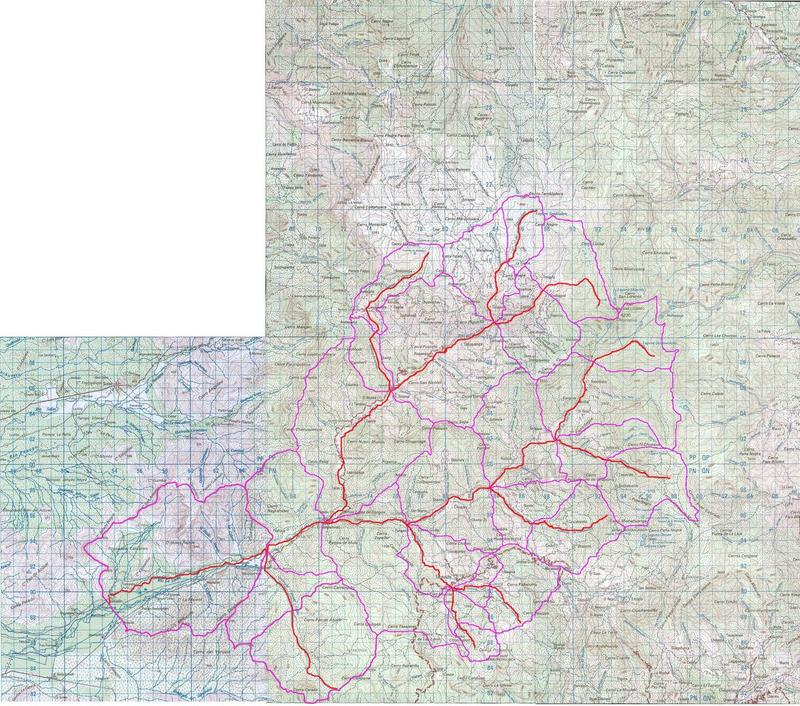Fig. 7   Cuenca del río La Leche, mostrando la red hidrográfica en rojo y los límites de las subcuencas en morado. 6.3   Pendientes del terreno Las pendientes del terreno a través de la cuenca La Leche se muestrearon en una malla de 1 km2. Las pendientes medias del terreno se muestran en el Cuadro 5. Las pendientes medias del terreno varían entre un mínimo de 19.7% en la Quebrada Tembladera y un máximo de 50.3% en el río Sangana 2, con un promedio de 33.7% para toda la cuenca La Leche [a La Calzada] (Fig. 8). 6.4   Lluvias de evento Las lluvias de evento [o tormentas] se definen en términos de la profundidad, duración, tipo y frecuencia. La longitud hidráulica en la cuenca de La Leche es de aproximadamente 44,600 m. Dada la alta rugosidad presente en la mayoría de las quebradas y ríos, las velocidades medias durante las inundaciones varían entre 3 y 4 m/s (Fig. 14). Por lo tanto, el tiempo de concentración varía entre 3 y 4 hr. De acuerdo a prácticas establecidas, la duración de la tormenta del diseño es de 24 hr (Ponce, 1989). Las tormentas tipo de 24 hr [NRCS] contienen las tormentas más cortas, desde 0.5 horas hasta 12 horas. Para elegir un tipo de tormenta, las características climatologías y geográficas de la cuenca La Leche se comparan con las cuatro regiones en los Estados Unidos para las cuales se han desarrollado tormentas tipo. La tormenta Tipo I, aplicable al Sur y Centro de la costa de California, una región árida/semiárida cercana al Océano Pacífico, pero con características orográficas importantes, se juzga muy similar a las condiciones locales y regionales de la cuenca La Leche. En el caso de la cuenca La Leche, para lo cual un valor generalizado de la Precipitación Máxima Probable (PMP) no está disponible, es práctica común sustituir el período de retorno de 10,000 años. Por lo tanto, las precipitaciones de diseño para represas grandes en la cuenca La Leche son las siguientes (Servicio de Conservación de los Recursos Naturales, 1985a; Ponce, 1989): Hidrograma del vertedero principal: Phvp = P100 Hidrograma del vertedero de emergencia: Phve = P100 + 0.26 (P10,000 - P100) Phve = 0.74 P100 + 0.26 P10,000 Hidrograma del borde libre: Phbl = P10,000 El hidrograma del vertedero principal se utiliza para determinar: (1) la capacidad del vertedero principal, (2), la elevación de la cresta del vertedero de emergencia, y (3) el volumen del almacenamiento de retención. El hidrograma del vertedero de emergencia se utiliza para determinar: (1) la capacidad del aliviadero de emergencia, (2), la máxima elevación de diseño del pelo de agua, y (3) el volumen de almacenamiento de detención. El hidrograma de borde libre se utiliza para determinar la elevación mínima de la cresta de presa y para evaluar la integridad estructural del sistema de vertederos (Fig. 9). Fig. 8   Pendientes típicas de la cuenca del río Moyán. Fig. 9   Niveles y volúmenes de almacenamiento en un reservorio (Ponce, 1989). Las tormentas máximas de 24 horas para las estaciones de Puchaca, Tocmoche, e Incahuasi, hasta 1998, se obtuvieron de Pérez Becerra (2006). El resto del registro (hasta el año 2002 para Puchaca, y 2007 para Tocmoche e Incahuasi), se obtuvo en el SENAMHI. Los valores ordenados se muestran en el Cuadro 6. 6.5   Grupos hidrológicos de suelo Los grupos hidrológicos de suelo para la cuenca de La Leche han sido estimados por el Consorcio Salzgitter-Lagesa (1984) de la siguiente manera: D para la cuenca superior, y B para las cuencas media y baja. Pérez Becerra (2006) ha estimado los grupos hidrológicos de suelo variando entre B, C y D, con tres tipos de usos de la tierra: (1) suelo o roca impermeable, (2) pastizales, y (3) arbustos. El promedio de veintiocho (28) subcuencas consideradas por Becerra Pérez es CNII = 85. Mientras esté pendiente la verificación de campo, el grupo hidrológico del suelo para toda la cuenca La Leche se ha estimado como D (afloramientos rocosos y suelo arcilloso). El uso de la tierra predominante es una mezcla de bosques/pastizales y tierras de cultivo (Fig. 10). El porcentaje de cobertura aérea y la condición hidrológica de la superficie se ha estimado utilizando el software GoogleEarth Pro©. Los valores de la tabla CNII son dados por Ponce (1989), entre otros. Fig. 10   Uso de la tierra en la cuenca Moyán. El Cuadro 7 muestra los valores ponderados de CNII. Los valores de la última columna de este cuadro se ponderan con las respectivas áreas de las subcuencas de drenaje para obtener un valor para toda la cuenca CNII = 83 [mostrado en la última fila de la última columna]. Este valor es un poco menor que el valor medio de Pérez Becerra (2006). Se asume la condición de humedad antecedente AMCIII (Ponce, 1989); por tanto, esto corresponde a CNIII = 93. Las condiciones asumidas de los grupos hidrológicos de suelo y condición hidrológica de la superficie quedan por verificar en el campo. 6.6   Número de Manning Los coeficientes de fricción de Manning se muestran en el Cuadro 8 (Barnes, 1967). Las observaciones de campo indican que los afluentes del río La Leche son capaces de mover grandes cantos rodados, algunos de más de 1 m de diámetro (Fig. 18). Los valores de los números de Manning para la mayoría de los tramos se toman como 0.075, y se muestran en el Cuadro 8. 6.7   Secciones transversales Los datos sobre las secciones transversales se están recolectando actualmente. En espera de la terminación del trabajo de campo, las secciones transversales típicas se estimaron para todas las subcuencas de tramo utilizando el orden y las áreas de drenaje, con el apoyo de observaciones de campo. Las estimación de secciones transversales se muestra en el Cuadro 8 y el Cuadro 9. 6.8   Trabajo en proceso Se está trabajando para verificar y completar los grupos hidrológicos de suelo, las condiciones hidrológicas de la superficie, y los datos de fricción y secciones transversales. 7.   FRECUENCIA DE PRECIPITACIONES La modelación de la frecuencia de precipitaciones se realizó utilizando los métodos de Log Pearson III y Gumbel (U.S. Interagency Advisory Committee on Water Data, 1983; Ponce, 1989). Los valores mostrados en el Cuadro 6 se utilizaron para calcular las tormentas de 24 horas, de 100 y 10,000 años, para las tres estaciones: Puchaca, Tocmoche, e Incahuasi. Estos valores se muestran en el Cuadro 10, junto con los valores adoptados, tomados como la media de los dos métodos. También se muestran en el Cuadro 10 las precipitaciones de 24 horas para el hidrograma del vertedero principal, vertedero de emergencia, y borde libre (Sección 6.4). Las tormentas de diseño de 100 y 10,000 años, y los datos de elevación mostrados en el Cuadro 10 se tomaron como referencia. Para cada subcuenca, las tormentas de diseño fueron obtenidas por interpolación logarítmica, dada la elevación del centroide de la subcuenca. Las tormentas de diseño se muestran en el Cuadro 11. Ponderando las tormentas con las respectivas áreas de drenaje conduce a la tormenta de diseño aplicable a toda la cuenca, mostrada en la última fila del Cuadro 11. 8.   RESULTADOS DEL MODELO Las tormentas de diseño del Cuadro 11 son utilizadas para correr el modelo RAINFLO©. Los números de la curva se muestran en el Cuadro 7. Se asume la condición antecedente de humedad AMCIII. La transformación de precipitación en escorrentía se efectúa utilizando los datos del Cuadro 4 y el Cuadro 5. Las velocidades medias se estiman en el rango 3-4 m/s. Los datos de fricción y secciones transversales se muestran en el Cuadro 8 y el Cuadro 9. El modelo se ha corrido por un período de 48 horas utilizando un intervalo de tiempo de 7.5 minutos. Para asegurar la precisión del método de tránsito de avenidas, los números de Courant se verificaron en el rango 0.5 ≤ C ≤ 2.0 (Ponce y Theurer, 1982; Ponce, 1989). 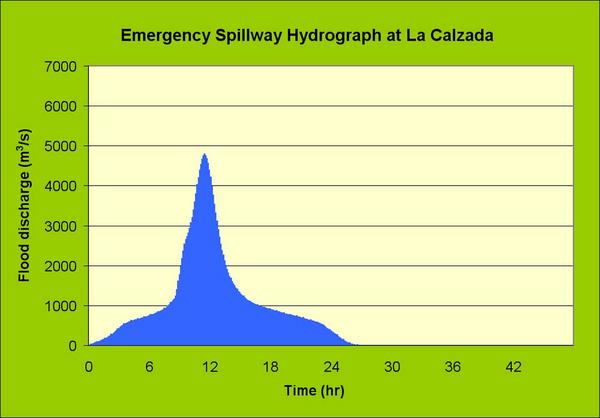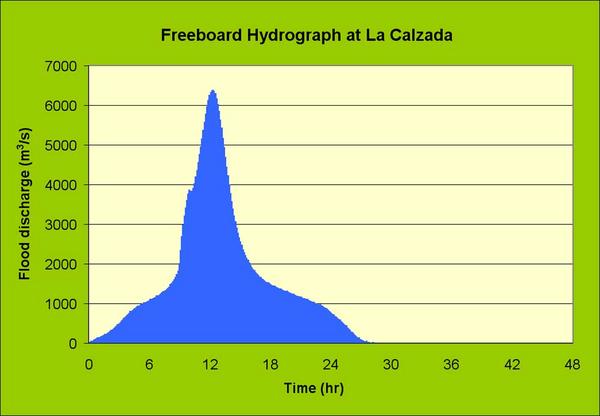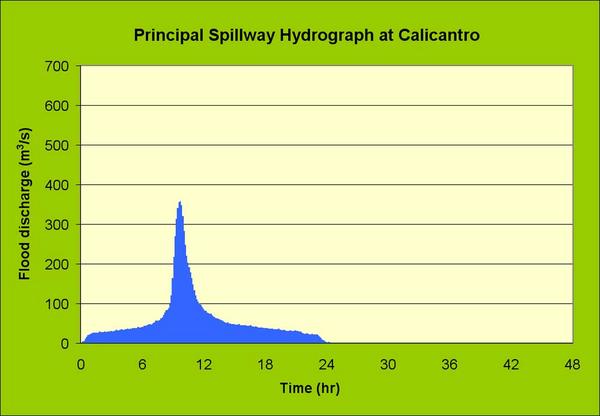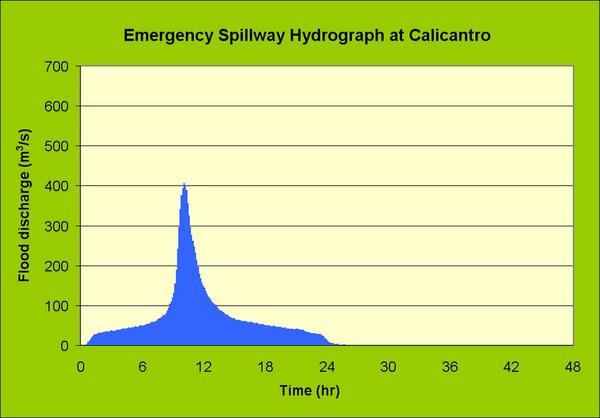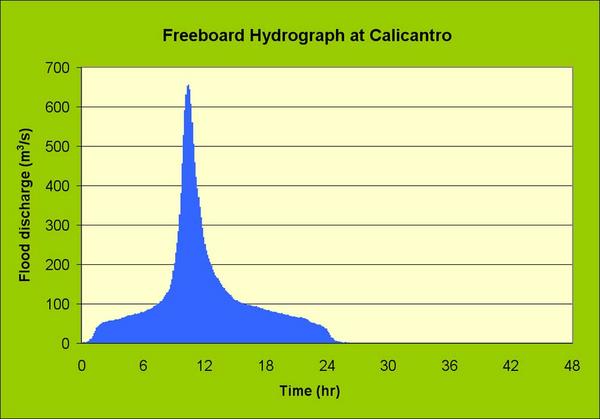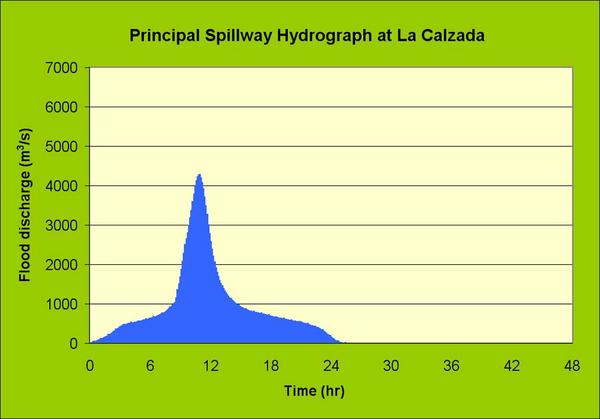Los hidrogramas de diseño se muestran en las Figuras 11, 12, y 13. El Cuadro 12 muestra un resumen de los caudales de avenida de diseño. Fig. 11   Hidrograma del aliviadero principal en La Calzada. Fig. 12   Hidrograma del aliviadero de emergencia en La Calzada. Fig. 13   Hidrograma del borde libre en La Calzada. Cuadro 12.   Caudales de avenida para la presa en La Calzada. Hidrograma Caudal de avenida (m3/s) Volumen del hidrograma (hm3) Tormenta de 24 horas (mm) Volumen de escorrentía (hm3) Escorrentía (%) Hidrograma del aliviadero principal 4,077 90 119 108 0.83 Hidrograma del aliviadero de emergencia 4,590 112 144 131 0.86 Hidrograma de borde libre 6,261 175 214 194 0.90 9.   PRESA EN CALICANTRO Se realizó una evaluación de los hidrogramas de diseño para la presa y embalse propuestos en Calicantro. La delimitación de la cuenca se muestra en la Fig. 14. El eje de la presa se encuentra donde hay un antiguo muro, llamado "Muro" en Rinconada Calicantro (Fig. 14). El modelo RAINFLO© fue utilizado para calcular los caudales de diseño. Se consideraron dos subcuencas: una subcuenca de cabecera [1], aguas arriba de La Tranca, y una subcuenca de tramo [10101], en Rinconada Calicantro propiamente dicha. Los procedimientos son los mismos que los utilizados para La Calzada (Véase la Sección 6). La tormenta de diseño en Calicantro se asumió igual que el valor para la estación de Puchaca. Los datos de Calicantro se muestra en el Cuadro 13 (propiedades hidrológicas), Cuadro 14 (números de la curva), Cuadro 15 (coeficientes de Manning), Cuadro 16 (datos de secciones transversales), y Cuadro 17 (tormentas de diseño). Los hidrogramas de avenida de diseño se muestran en las Figs. 14, 15 y 16, estando pendiente la verificación en el campo del tipo de suelo y los datos de las secciones transversales. El Cuadro 18 muestra un resumen de los caudales de avenida de diseño. Fig. 14  Delimitación de la cuenca para la presa Calicantro. Fig. 15   Hidrograma del aliviadero principal en Calicantro. Fig. 16   Hidrograma del aliviadero de emergencia en Calicantro. Fig. 17   Hidrograma del borde libre en Calicantro. Cuadro 18.   Caudales de avenidas para la presa en Calicantro. Hidrograma Caudalde avenida (m3/s) Volumen del hidrograma (hm3) Tormenta de 24 horas (mm) Volumen de escorrentía (hm3) Escorrentía (%) Hidrograma del aliviadero principal 359 5.28 207 6.08 0.87 Hidrograma del aliviadero de emergencia 406 6.82 260 7.64 0.89 Hidrograma del borde libre 656 11.18 409 12.01 0.93 10.   CONCLUSIONES Se ha utilizado un modelo computacional, determinístico/conceptual, distribuído, de precipitación-escorrentía para calcular los caudales de diseño aplicables a los vertidos de la presa en el río La Leche en La Calzada, en Lambayeque, Perú. Tambien se han efectuado los cálculos para el proyecto de sitio de presa en la localidad vecina de Calicantro (Sección 9). El modelo está impulsado por tormentas máximas de 24 horas, las cuales toman en cuenta todo el registro de precipitaciones, incluyendo los episodios de El Niño (Fig. 1). Estos fenómenos meteorológicos, los cuales suelen repetirse cada 12 a 15 años, producen grandes cantidades de precipitación. Las inundaciones resultantes amenazan a los asentamientos humanos existentes en la parte baja de la cuenca del río La Leche. Los datos geométricos, hidrológicos, del suelo, de la fricción, y las secciones transversales son ensambladas en forma adecuada para alimentar al modelo computacional. Se ha calculado el pico de las avenidas, los volúmenes de los hidrogramas, los volúmenes de las tormentas, y el porcentage de escorrentía, aplicables al diseño del vertedero principal, vertedero de emergencia, y borde libre (Cuadros 12 y 18). Estos hidrogramas pueden ser utilizados para dimensionar el tamaño del almacenamiento de retención, el almacenamiento de detención, y el borde libre (Fig. 9). BIBLIOGRAFÍA Barnes, H. A. 1967. Roughness characteristics of natural channels. U.S. Geological Survey Water-Supply Paper 1849, Washington, D.C. Consorcio Salzgitter-Lagesa, 1984. Rehabilitación y reconstrucción de los sistemas de riego y drenaje del valle Chancay-Lambayeque: Estudio de evacuación de avenidas extraordinarias a nivel de factibilidad técnica. Tomo 1: Resumen e investigaciones básicas, marzo. Cunge, J. A., 1969. On the subject of a flood propagation computation method (Muskingum method). Journal of Hydraulic Research, Vol. 7, No. 2, 205-230. DEPOLTI (Dirección Ejecutiva del Proyecto Especial Olmos-Tinajones), 1998. Actualización de la factibilidad tecnico-económica del embalse en el río La Leche, Chiclayo, Peru, 339 p. Hayami, S., 1951. On the propagation of flood waves. Disaster Prevention Research Institute, Kyoto University, Bulletin No. 1, December. Horton, R, E., 1933. The role of infiltration in the hydrologic cycle. Transactions, American Geophysical Union, Vol. 14, 446-460. Natural Resources Conservation Service, 1985a. Earth dams and reservoirs. Technical Release No. 60 (TR-60), revised October. Natural Resources Conservation Service, 1985b. National Engineering Handbook, Section No. 4 - Hydrology, Washington, D.C. Perez Becerra, M. A., 2006. Estudio hidrológico e hidráulico en el río La Leche: Generación de las descargas y niveles máximos por avenidas en la zona del proyecto "Puente Colgante Pítipo." Proyecto Especial Olmos-Tinajones, Gerencia de Desarrollo Tinajones, Mayo. Ponce, V. M., y D. B. Simons, 1977. Shallow wave propagation in open channel flow. ASCE Journal of Hydraulic Engineering, Vol. 103, No. 12, December. Ponce, V. M., y V. Yevjevich, 1979. Muskingum-Cunge method with variable parameters. ASCE Journal of Hydraulic Engineering, Vol. 103, No. 12, December. Ponce, V. M., y F. D. Theurer, 1982. Accuracy criteria in diffusion routing. ASCE Journal of Hydraulic Engineering, Vol. 108, No. 6, June. Ponce, V. M., 1985. Large basin deterministic hydrology: A case study. ASCE Journal of Hydraulic Engineering, Vol. 111, No. 9, September. Ponce, V. M., 1989. Engineering Hydrology, Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey. Ponce, V. M., y R. H. Hawkins, 1996. Runoff curve number: Has it reached maturity? ASCE Journal of Hydrologic Engineering, Vol. 1, No. 1, January. Seddon, J. A., 1900. River hydraulics. ASCE Transactions, Vol. XLIII, 179-243, June. Ponce, V. M., H. A. Castro, A. E. Espinoza, R. Celis, y F. Perez. 2005. Flood hydrology of Tecate Creek, Tecate, Baja California, Mexico. Web report. U.S. Interagency Advisory Committee on Water Data, 1983. Guidelines for determining flood flow frequency. Hydrology Subcommitee, Bulletin No. 17B, issued 1981, revised 1983, Reston, Virginia. Fig. 18   El río Moyán, mostrando la presencia de grandes cantos rodados en su lecho. Cuadro 1   Cuadro 2    Cuadro 3    Cuadro 4    Cuadro 5    Cuadro 6    Cuadro 7    Cuadro 8    Cuadro 9    Cuadro 10 Cuadro 11    Cuadro 12    Cuadro 13    Cuadro 14    Cuadro 15    Cuadro 16    Cuadro 17    Cuadro 18    Cuadros

080702