CLOSED CONDUITS II CHAPTER 5 (3) - ROBERSON ET AL., WITH ADDITIONS INSTRUMENTS AND PROCEDURES FOR DISCHARGE MEASUREMENT DIRECT METHODS INVOLVE MEASURING THE ACTUAL QUANTITY OF FLOW FOR A GIVEN TIME INTERVAL. DIRECT VOLUME/WEIGHT MEASUREMENT: VOLUME/WEIGHT IN A PERIOD OF TIME. INDIRECT METHODS MEASURE PRESSURE OR OTHER VARIABLE RELATED TO RATE OF FLOW. FLOW THROUGH ORIFICES, VENTURI METERS, AND FLOW NOZZLES. VELOCITY-AREA INTEGRATION METHOD: dQ = V dA WHERE dQ = INCREMENTAL DISCHARGE V = LOCAL VALUE OF VELOCITY dA = INCREMENTAL FLOW AREA IN A PIPE, AT RADIUS r, THE INCREMENTAL AREA IS: dA = 2 π r dr THEREFORE: dQ = V 2 π r dr = 2 π V r dr Q MAY BE OBTAINED BY INTEGRATION. Q = ∫ dQ = ∫ 2 π V r dr = 2 π ∫ V r dr WHERE r VARIES FROM 0 to ro. VELOCITY SHOULD BE SYMMETRICAL IN PIPE. ORIFICE A RESTRICTED OPENING THROUGH WHICH FLUID FLOWS IS AN ORIFICE. THE ORIFICE CAN BE USED TO MEASURE FLOW RATES. MINIMUM FLOW AREA THROUGH ORIFICE IS ACTUALLY SMALLER THAN THE AREA OF THE ORIFICE. 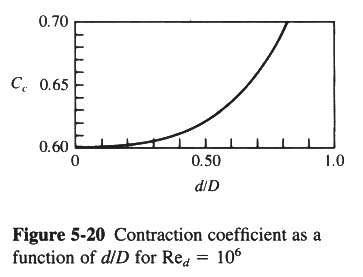AREA OF THE ORIFICE Ao MINIMUM FLOW AREA Aj CONTRACTION COEFFICIENT Cc = Aj /Ao CONTRACTION COEFFICIENT Cc = (dj/d)2 CONTRACTION COEFFICIENT Cc = A2 /Ao AT LOW Re, Cc IS A FUNCTION OF Re. AT HIGH Re, Cc IS ONLY A FUNCTION OF THE GEOMETRY OF THE ORIFICE. FIG. 5-20 SHOWS Cc AS A FUNCTION OF d/D, WHERE D IS THE PIPE DIAMETER, FOR Red = 106. DISCHARGE EQUATION FOR THE ORIFICE: h1 + V12/(2g) = h2 + V22/(2g) V1A1 = V2A2 h1 + [V22/(2g)](A2/A1)2 = h2 + V22/(2g) V22[1 - (A2/A1)2] = 2g (h1 - h2) V2 = { 2g (h1 - h2) / [1 - (A2/A1)2]}   0.5 Q = A2V2 = A2 { 2g (h1 - h2) / [1 - (A2/A1)2] }   0.5 Q = {Cc Ao/ [1 - (CcAo/A1)2] 0.5 }   [2g (h1 - h2)] 0.5 THIS EQUATION IS ONLY VALID AT HIGH Re. FOR LOW AND MODERATE Re, VISCOUS EFFECTS MAY BE SIGNIFICANT. ADDITIONAL COEFFICIENT IS APPLIED. COEFFICIENT OF VELOCITY Cv: Q = {Cv Cc Ao/ [1 - (CcAo/A1)2] 0.5}   [2g (h1 - h2)] 0.5 THE PRODUCT Cv Cc IS CALLED THE DISCHARGE COEFFICIENT Cd Q = {Cd Ao/ [1 - (CcAo/A1)2] 0.5 } [2g (h1 - h2)] 0.5 THE FLOW COEFFICIENT K IS K = Cd / [1 - (CcAo/A1)2] 0.5 THEREFORE: Q = K Ao [2g (h1 - h2)] 0.5 Δh = h1 - h2 Q = K Ao (2g Δh) 0.5 THE DIFFERENCE IN PRESSURE IS Δp = γΔh. FIG. 5-21 SHOWS EXPERIMENTALLY DETERMINED VALUES OF K AS A FUNCTION OF d/D AND REYNOLDS NUMBER Red BASED ON ORIFICE SIZE. Ao = πd2/4 Red = Vd/ ν = Qd/(Ao ν) = Qd/[(πd2/4) ν] = 4Q /(πd ν) K = Q / [Ao (2g Δh) 0.5] Red / K = [4Q /(πd ν)] / {Q / [Ao (2g Δh) 0.5]} Red / K = 4 Ao (2g Δh) 0.5 /(πd ν) Red / K = d2 (2g Δh) 0.5/ (d ν) Red / K = (2g Δh) 0.5(d / ν) PROBLEM 1 TO DETERMINE Δh FOR DISCHARGE Q THROUGH ORIFICE OF DIAMETER d AND PIPE OF DIAMETER D, AND ν 1.   Calculate Red = 4Q /(πd ν) 2.   Obtain K from Fig. 5-21 for Red and d/D 3.   Since Q = K Ao (2g Δh) 0.5 4.   Δh = [Q/ (K Ao)] 2 / (2g) PROBLEM 2 TO DETERMINE Q FOR DROP Δh THROUGH ORIFICE OF DIAMETER d AND PIPE OF DIAMETER D, AND ν. 1.   Calculate Red / K = (2g Δh) 0.5(d / ν) 2.   Obtain K from Fig. 5-21 with Red / K and d/D 3.   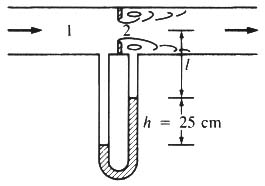Solve for Q:   Q = K Ao (2g Δh)0.5 EXAMPLE 5-9 A 15-CM ORIFICE IS LOCATED IN A HORIZONTAL 24-CM WATER PIPE. WHEN THE DEFLECTION IN THE WATER-MERCURY MANOMETER IS 25 CM, WHAT IS THE DISCHARGE? ASSUME WATER TEMPERATURE IS 20oC. SOLUTION MANOMETER EQUATION. SPECIFIC GRAVITY OF MERCURY:  γHg/γw = 13.6 SPECIFIC GRAVITY OF WATER:  γw/γw = 1. CALCULATE HEIGHT OF WATER COLUMN Δh: P1 + γwh1 = P2 + γwh2 + γHgh P1 - P2 = γw(h2 - h1) + γHgh Δh = Δp/γw = - h + (γHg/γw) h Δh = Δp/γw = 12.6 h EVALUATE Δh = 12.6 × 0.25 = 3.15 M COMPUTE Red / K = (2g Δh)0.5(d/ ν) = [(2) (9.81) (3.15)]0.5 (0.15 / 1.0 × 10-6 ) = 1.2 × 106 COMPUTE d/D = 0.15/0.24 = 0.625 FROM FIG. 5-21: K = 0.66 Q = K Ao (2g Δh)0.5 = 0.66 [0.25 π (0.15)2] [(2) (9.81) (3.15)] 0.5 Q = 0.092 M3/S. ON THE OTHER HAND, ASSUME Q = 0.092 M3/S, FIND Δh. CALCULATE Red = 4Q /(πd ν) Red = 4(0.092) /[(3.1416)(0.15)(1.0 × 10-6)] = Red = 780,918 FOR d/D = 0.625, FROM FIG. 5-21: K = 0.66 Δh = [Q/ (K Ao)] 2 / (2g) = Δh = {0.092/ [(0.66)(0.25)(3.1416)(0.15)2]}2/ (19.62)= Δh = 3.17 M (H2O) = 3.17/(13.6 - 1) = 0.251 M (Hg) VENTURI METER THE ORIFICE IS SIMPLE, BUT THE HEAD LOSS IS QUITE LARGE. IT IS LIKE AN ABRUPT ENLARGEMENT IN A PIPE. THE VENTURI METER OPERATES ON THE SAME PRINCIPLE AS THE ORIFICE, BUT WITH A SMALLER HEAD LOSS. THE LOWER HEAD LOSS RESULTS FROM STREAMLINING THE FLOW PASSAGE. THE STREAMLINING ELIMINATES ANY THE JET CONTRACTION BEYOND THE SMALLEST FLOW SECTION. COEFFICIENT OF CONTRACTION Cc HAS A VALUE OF UNITY. Q = {A2 Cd / [1 - (A2/A1)2] 0.5} [2g (h1 - h2)] 0.5 K = Cd / [1 - (A2/A1)2] 0.5 Q = K A2 (2g Δh) 0.5 THIS EQUATION IS THE SAME AS THAT OF THE ORIFICE, BUT K IS MUCH HIGHER. K OBTAINED ALSO FROM FIG. 5-21. FOR THE VENTURI METER, K APPROACHES 1 FOR HIGH Re AND RELATIVELY SMALL d/D RATIOS (d/D = 0.4) K CAN EXCEED UNITY FOR LARGE d/D RATIOS (d/D = 0.6). FORCES AND STRESSES IN PIPES AND BENDS FORCES ON BENDS AND PIPE TRANSITIONS THERE IS A CHANGE IN MOMENTUM IN FLOW AROUND A BEND. A MOMENTUM EQUATION IS USED TO CALCULATE THE FORCES ACTING ON BENDS AND TRANSITIONS. GENERAL MOMENTUM EQUATION: &sum Fsystem = ∑ V ρ (V • A) UNITS:   N = [M/S] {[N/M3]/[M/S2]} [M3/S] THE FORCES ARE EXTERNAL FORCES SUCH AS PRESSURE OF WATER, GRAVITY AND THE UNKNOWN FORCE TO HOLD THE BEND IN PLACE. EQUATION WRITTEN IN SCALAR FORM: ∑ Fx = ρ Q (V2x - V1x) ∑ Fy = ρ Q (V2y - V1y) ∑ Fz = ρ Q (V2y - V1y) EXAMPLE A 1-M DIAMETER PIPE HAS A 30o HORIZONTAL BEND AND CARRIES WATER (10oC) AT THE RATE OF 3 M3/S. PRESSURE IN THE BEND IS UNIFORM AT 75 kPa [75000 N/M2]. THE VOLUME OF THE BEND IS 1.8 M3. THE METAL IN THE BEND WEIGHS 4 kN. WHAT FORCE MUST BE APPLIED TO THE BEND BY THE ANCHOR TO HOLD THE BEND IN PLACE? ASSUME EXPANSION JOINTS PREVENT ANY FORCE TRANSMITTAL THROUGH THE PIPE WALLS. SOLUTION: SOLVE FOR THE X-COMPONENT OF THE FORCE: ∑ Fx = ρ Q (V2x - V1x) p1A1 - p2A2 cos 30o + Fanchor,x = [(9810 N/M3)/(9.81 M/S2)] (3 M3/S) (V2x - V1x) (M/S) A1 = A2 = (π/4) D2 = 0.785 M2 V2x = (Q/A2) cos 30o = (3/0.785) (0.866) = 3.31 M/S V1x = Q/A1 = 3/0.785 = 3.82 M/S p1A1 - p2A2 cos 30o + Fanchor,x = 3000 (3.31 - 3.82) p1A1 - p2A2 cos 30o + Fanchor,x = - 1530 Fanchor,x = - 1530 - p1A1 + p2A2 cos 30o p1 = p2 = 75000 N/M2 Fanchor,x = - 1530 - 75000 (A1 - A2 cos 30o) A2 cos 30o = 0.785 (0.866) Fanchor,x = -1530 - 75000 (0.785) (1 - 0.866) Fanchor,x = -1530 - 7890 Fanchor,x = - 9420 N BOTH PRESSURE DIFFERENCE (-7890) AND MOMENTUM DIFFERENCE (-1530) CAUSE FORCE APPLIED BY ANCHOR TO THE BEND TO BE NEGATIVE (NEGATIVE X, TO THE LEFT IN THE FIGURE). SOLVE FOR THE Y-COMPONENT OF THE FORCE: ∑ Fy = ρ Q (V2y - V1y) p2A2 sin 30o + Fanchor,y = [(9810 N/M3)/(9.81 M/S2)] (3 M3/S) (V2y) (M/S) V2y = - (Q/A2) sin 30o = - (3/0.785) (0.5) = - 1.91 M/S NOTE THAT THE SIGN OF V2y IS NEGATIVE BECAUSE IT IS DOWNWARDS IN FIG B, OPPOSITE TO p2, WHICH IS UPWARDS, I.E., POSITIVE. A2 sin 30o = 0.785 (0.5) = 0.3925 Fanchor,y = 3000 (-1.91) - 75000 (0.3925) Fanchor,y = -5730 - 29440 = - 35170 N BOTH PRESSURE DIFFERENCE (-29940) AND MOMENTUM DIFFERENCE (-5730) CAUSE FORCE APPLIED BY ANCHOR TO THE BEND TO BE NEGATIVE (NEGATIVE Y, DOWNWARDS IN THE FIGURE). SOLVE FOR THE Z-COMPONENT OF THE FORCE: ∑ Fz = ρ Q (V2z - V1z) Wbend + Wwater + Fanchor,z = ρ Q (V2z - V1z) = 0 - 4000 N - (9810 N/M3)(1.8 M3) + Fanchor,z = 0 NOTE THAT FORCES ARE POSITIVE UP, IN THE DIRECTION CONTRARY TO GRAVITY. Fanchor,z = 4000 + 17660 = 21660 N BOTH THE WEIGHT OF THE BEND (4000 N) AND THE WEIGHT OF THE WATER (17600 N) CAUSE THE VERTICAL FORCE APPLIED BY THE ANCHOR TO THE BEND TO BE POSITIVE (UPWARDS, AGAINST GRAVITY). Fanchor = -9.42 i - 35.17 j + 21.66 k       [KILONEWTONS] CAVITATION EFFECTS CAVITATION OCCURS IN FLOWING LIQUIDS WHEN THE FLOW PASSES THROUGH A ZONE IN WHICH THE PRESSURE BECOMES EQUAL TO THE VAPOR PRESSURE OF THE LIQUID, AND THEN THE FLOW CONTINUES ON TO A REGION OF HIGHER PRESSURE. VAPOR BUBBLES FORM, AND WHEN THESE BUBBLES ENTER THE ZONE OF HIGH PRESSURE, THEY COLLAPSE AND CAN LEAD TO EQUIPMENT FAILURE. 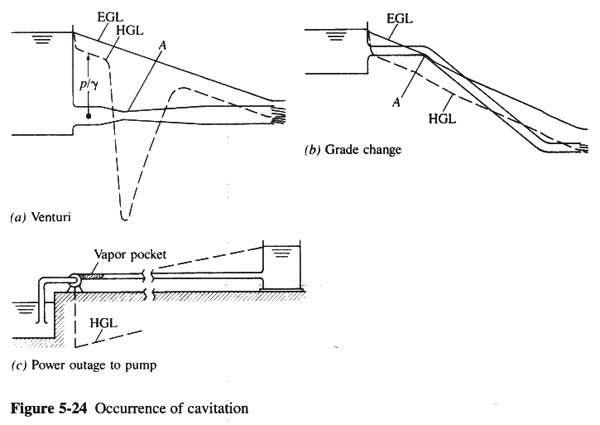HIGH VELOCITY THROUGH VENTURI IS ACCOMPANIED BY REDUCED PRESSURE [FIG. 24 (a)]. PIPE ELEVATION CHANGE AND HEAD LOSS ALONG THE PIPE MAY LEAD TO NEGATIVE PRESSURES [FIG. 24 (b)]. IN PUMPS, IF POWER IS INTERRUPTED, HGL CAN FALL BELOW PIPE [FIG. 24 (c)]. GOOD HYDRAULIC DESIGN NORMALLY EXCLUDES THE POSSIBILITY OF CAVITATION. CAVITATION WILL OCCUR IF THE PRESSURE HEAD GETS CLOSE TO -33.9 FT (ABSOLUTE ZERO). (THE HYDRAULIC GRADE LINE IS AT ELEVATION -33.9 FT BELOW THE POINT IN QUESTION). USBR RECOMMENDS THAT THE PRESSURE HEAD THROUGHOUT THE PIPE SYSTEM SHOULD BE GREATER THAN -1O FT. 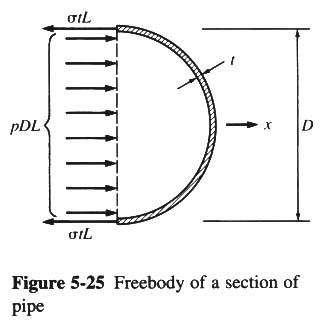PIPE STRESSES DUE TO INTERNAL PRESSURE IN THIN-WALLED PIPES, THE RATIO OF THICKNESS t TO DIAMETER D IS:   t/D < 0.1 ASSUME UNIFORM DISTRIBUTION OF STRESSES IN THE WALL OF A THIN-WALLED PIPE. FREE-BODY DIAGRAM:   ∑ Fx = 0 pDL = 2σ t L σ = pD / (2t) r = D/2 σ = pr/t IN THIN-WALLED PIPES, THE STRESS σ IS PROPORTIONAL TO THE RATIO r/t. STRESS IN THICK-WALLED PIPES: r = radius to point inside pipe wall ri = inside radius ro = outside radius σ = [(pri2) /(ro2 - ri2)] [1 + (ro2/r2)] EXTERNAL LOADING PIPES THAT ARE LAID ON A TRENCH MUST BE DESIGNED FOR EXTERNAL LOADING ALSO. THIS IS PARTICULARLY THE CASE WHEN THE INTERNAL PRESSURE IS LOW. EMPIRICAL PROCEDURE: MARSTON FORMULA: W = C γsB2 W = VERTICAL LOAD ACTING ON PIPE, PER UNIT LENGTH [N/M OR LB/FT] C = COEFFICIENT, A FUNCTION OF RELATIVE FILL HEIGHT AND SOIL TYPE γs = UNIT WEIGHT OF SOIL [N/M3] B = TRENCH WIDTH OR CONDUIT WIDTH [M] RIGID PIPE INSTALLATION (FOR CONCRETE PIPES) MARSTON FORMULA: W = C γsBb2 Bd = TRENCH WIDTH [M] FIG 5-28 SHOWS COEFFICIENT C, AS A FUNCTION OF SOIL AND RELATIVE HEIGHT OF SOIL COVER H/Bd. FLEXIBLE PIPE INSTALLATION (FOR STEEL OR PLASTIC PIPES) IF THE SOIL AT THE SIDES IS WELL COMPACTED, THE SIDE WALLS WILL CARRY A SIGNIFICANT PORTION OF THE TOTAL LOAD: MARSTON FORMULA IS MODIFIED TO: W = C γsBdBc Bd = TRENCH WIDTH [M] Bc = CONDUIT DIAMETER [M] FIG 5-28 SHOWS COEFFICIENT C, AS A FUNCTION OF SOIL AND H/Bd. THIS PROCEDURE FOR LOAD DETERMINATION IS APPLICABLE WHEN PIPES ARE LAID IN RELATIVELY NARROW TRENCHES:   Bd < 2Bc IF Bd > 2Bc, THE CALCULATED LOAD WILL BE TOO LARGE, AND ANOTHER PROCEDURE MUST BE USED. IF LIVE LOADS ARE A FACTOR, THEY TOO MUST BE CONSIDERED. THE STRENGTH OF RIGID PIPES THE STRENGTH OF RIGID PIPES SUCH AS CONCRETE OR CLAY IS DETERMINED BY A [STANDARD] THREE-EDGED BEARING TEST PERFORMED IN THE LABORATORY. HOWEVER, THE ACTUAL FIELD STRENGTH OF THE PIPE WILL DEPEND ON BEDDING CONDITIONS. THEREFORE, THE PIPE STRENGTH BASED ON LAB TEST IS MODIFIED BY A LOAD FACTOR RELATING TO THE TYPE OF BEDDING. FOR EXAMPLE, FOR A THREE-EDGE BEARING STRENGTH ON PIPE = 6500 LB/FT (FROM TEST). A FIELD-SUPPORTING STRENGTH WITH A CLASS C BEDDING (FIG. 5-27) WOULD BE:   6500 × (LOAD FACTOR) = 6500 × 1.5 = 9750 LB/FT FACTOR OF SAFETY APPLIED: F.S. = 1.5 S(SAFE) = S(3-EDGE) × (LOAD FACTOR)/(F.S.) IN THIS EXAMPLE: STRENGTH OF CONDUIT = 6500 (1.5)/1.5 = 6500 LB/FT. PIPE MATERIALS -- STEEL -- DUCTILE IRON -- CONCRETE -- PLASTIC STEEL USED FOR PROJECTS IS GENERALLY OF MEDIUM CARBON CONTENT, WHICH HAS HIGH STRENGTH AS WELL AS HIGH DUCTILITY. USED FROM SMALL PIPES IN HOUSEHOLDS TO 12-FT AND LARGER PENSTOCKS OR PIPELINES. AWWA RECOMMENDS A TENSILE STRESS EQUAL TO 50% OF YIELD POINT STRESS. THE YIELD POINT RANGES FROM 25000 TO 45000 PSI, DEPENDING ON THE GRADE OF STEEL. SPECIAL COATINGS ARE USED TO PROVIDE CORROSION RESISTANCE. COMMONLY USED COATINGS ARE COAL TAR ENAMEL, POLYMERS, PLASTICS, CEMENT MORTAR, AND ZINC. CORRUGATED STEEL PIPE WAS DEVELOPED FOR HIGHWAY APPLICATIONS. CORRUGATED STEEL PIPE IS AVAILABLE IN DIAMETERS FROM 4 IN TO 144 IN. CONCRETE IS USED FOR STORM SEWERS AND SANITARY SEWERS, HIGHWAY AND RAILROAD CULVERTS, AND PRESSURE PIPES. DEPENDING ON THE LOAD, EITHER UNREINFORCED OR REINFORCED CONCRETE ARE USED. THE MOST COMMON TYPE OF PLASTIC PIPE IS PVC. PROPERTIES OF PVC: -- CORROSION RESISTANCE -- SMOOTHNESS (LESS RESISTANCE TO FLOW) -- EASE OF FIELD ASSEMBLY. Calleguas Brine Line under construction, Port Hueneme, California, August 2007. PVC IS USED EXTENSIVELY IN IRRIGATION AND SEWER SYSTEMS. UNDER HIGH PRESSURE, PVC IS REINFORCED WITH FIBERGLASS FOR ADDED STRENGTH. 091028