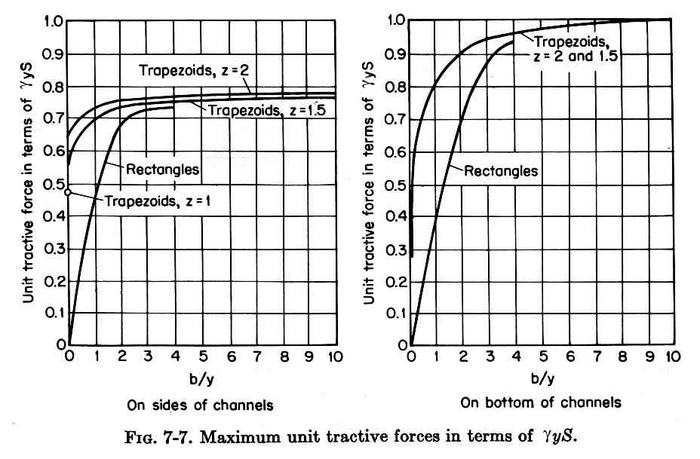
The acting shear stress on the sides:

T_s = 0.78 γ y S_o = (0.78) (62.4) (y) (0.00065) = 0.0316 y

Permissible tractive stress on level ground: τ_L = 0.2 lb/ft²

Permissible tractive stress on the sides: τ_s = K τ_L = (0.4472) (0.2) = 0.08944 lb/ft²

Under equilibrium: T_s = τ_s

Thus:

0.0316 y = 0.08944

From which flow depth y is:

y = 2.83 ft.

The Manning equation is:

Q = (1.486/n) A R^2/3 S^1/2 = (1.486/0.02) A (A^2/3/P^2/3) (S)^1/2

Q = (1.486/0.02) (A^5/3/P^2/3) (0.00065)^1/2

Q = 1.894 (A^5/3/P^2/3)

A = (b + zy) y = (b + 2y) y

P = b + 2 y (1+z²)^1/2 = b + 2 y (1+2²)^1/2 = b + 4.472 y

With y = 2.83 ft, try several values of b, until design Q is satisfied.

b	A	A5/3	P	P2/3	Q
60	185.82	6050.9	72.65	17.411	658.23
70	214.12	7663.4	82.65	18.975	764.92
74	225.44	8350.4	86.65	19.582	807.65

Choose b = 74 ft; y = 2.83 ft; from which b/y = 26 > 10.     OK.

With b/y = 26, the coefficient of tractive force based on material on the bottom:    C_b = 1.0

The acting shear stress on level ground is:

T_L= 1.0 γ y S_o = (1.0) (62.4) (2.83) (0.00065) = 0.115 lb/ft²

T_L= 0.115 < 0.2 = τ_L

Therefore, the sides control the design.

b= 74 ft; y = 2.83 ft.     ANSWER.