CIVE 530 - OPEN-CHANNEL HYDRAULICS

LECTURE 3: ENERGY AND MOMENTUM PRINCIPLES

3.1  ENERGY IN OPEN-CHANNEL FLOW


  • The total energy at a point A on a streamline is equal to:

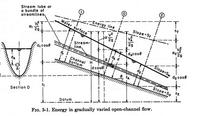
H = zA + dA cos θ + αVA2/(2g)

   [L]


Fig. 3-1 (Chow)


  • The total energy at the channel section is equal to:

    H = z + d cos θ + αV2/(2g)

    		   [L]

  • The conservation of energy between sections 1 and 2 leads to:

    z1 + y1 + α1V12/(2g) = z2 + y2 + α2V22/(2g) + hf

    		   [L]

  • In the Bernoulli equation: α1 = α2 = 1; hf = 0.

    z1 + y1 + V12/(2g) = z2 + y2 + V22/(2g) = constant

    		   [L]

  • The energy slope is:

    Se = hf/L

  • The friction slope is:

    Sf = hf'/L

  • Under steady flow, the friction slope is equal to the energy slope.

  • Under uniform flow, the friction, energy, bottom, and water-surface slopes are all the same.

    Sf = Se = So = Sw


3.2  SPECIFIC ENERGY


  • The specific energy is the energy [per unit of weight (mg)] measured with reference to the channel bottom:

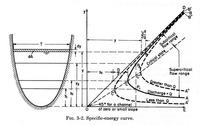
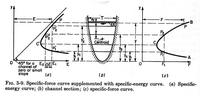
    E = d cos θ + αV2/(2g)

  • For α ≈ 1:

    E = y + V2/(2g)

  • Since Q= VA (continuity):

    E = y  +  Q2/(2gA2)

  • Since A= f1(y) (cross sectional area is a function of flow depth):

    E = y  +  Q2/[2g f1(y)]

    		  

    E = f2(y)

    		  (for a constant Q)


    Fig. 3-2 (Chow)

3.3  CRITICAL FLOW CRITERION: MINIMUM SPECIFIC ENERGY

  • The specific energy in terms of discharge Q and flow area A is:

    E = y  +  Q2/(2gA2)

  • To find the minimum specific energy, take the derivative of E and equate to zero (0):

    dE/dy = 1 - [Q2/(gA3)] (dA/dy) = 0

  • The differential of flow area A is:

    dA = T dy

  • Therefore:

    dA/dy = T

  • Therefore:

    (Q2 T) / (gA3) = 1

    V2/(gA/T) = 1

    V2/(gD) = 1

  • Therefore, for minimum specific energy:

    V2/(gD) = 1

  • The Froude number is:

    F = V/(gD)1/2

  • Thus, for minimum specific energy, the Froude number is:

    F = 1

  • Also, at critical state, the velocity head is:

    V2/(gD) = 1

    		[Critical state]

    V2/(2g) = D/2

  • When α ≠ 1:

    αV2/(2g) = D/2

  • When α ≠ 1 and cos θ ≠ 1:

    α V2/(2g) = (D cosθ)/2

  • The most general definition of Froude number is:

    F = V / [(gDcosθ)/α]1/2

3.4  INTERPRETATION OF LOCAL PHENOMENA


  • Changes in the state of flow from subcritical to supercritical or vice versa occur frequently in open channels.

  • If the change takes place over a short distance, the flow is rapidly varied, and is known as a local phenomenon.

  • The hydraulic jump and hydraulic drop are local phenomena.

  • The hydraulic jump changes from supercritical to subcritical flow.


Hydraulic jump on Tinajones outlet canal, Chiclayo, Peru

  • The hydraulic drop changes from subcritical to supercritical flow.

  • The hydraulic drop is caused by an abrupt change in the channel slope or cross section.

  • The free overfall is a special case of hydraulic drop.

  • The flow at the brink is actually curvilinear.

  • Hence, the method is invalid for determining the critical depth as the depth at the brink.

  • The brink section is the true section of minimum energy, but is it not the critical section as computed by the principle based on the parallel flow assumption.


    Fig. 3-3 (Chow)

  • The computed critical depth yc is:

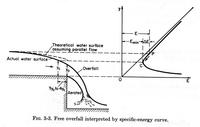
    yc = 1.4 yo

    where yo is the depth at the brink.

  • The hydraulic jump occurs frequently in a canal below a regulating sluice, at the foot of a spillway, or at the place where a steep channel suddenly turns flat.

  • There is energy loss in the jump.

  • The specific energy at the initial depth is always greater than the specific energy at the sequent depth.

  • The energy loss is referred to as ΔE.


    Fig. 3-4 (Chow)

  • The gradual hydraulic drop is not a local phenomenon.

  • The gradual hydraulic drop is caused by a narrowing of the cross section.

  • The narrowing of the cross section causes flow to change from subcritical upstream to supercritical downstream.

  • The point of inflection (zero curvature) marks the critical depth.  

     

3.5  ENERGY IN NONPRISMATIC CHANNELS

Example 3-1. Channel contraction with and without gradual hydraulic drop.

Discharge = 100 cfs.

Upstream flow depth = 5 ft.

Upstream channel width = 10 ft.

Downstream channel width = 8 ft.

Length of the contraction = 50 ft.

Assume the floor of the contraction is horizontal and the friction through the contraction is negligible.

Determine the water surface profile in the contraction:

(A) without gradual hydraulic drop, and

(B) with gradual hydraulic drop.

A. The specific energy in the upstream cross section is:

E = y  +  Q2/(2gA2) = 5  +  1002/[2g(10×5)2] = 5.062 ft

The velocity head upstream of the contraction is:   5.062 - 5 = 0.062 ft.

The specific energy at any section in the contraction is:   E = 5.062 ft.

5.062 = y  +  1002/[2g(by)2]

y3 - 5.062 y2 + (155.25/b2)

For b = 10 ft (upstream section):

y1 = 0.589 ft (low stage; alternate depth)

y2 = 5.000 ft (high stage; actual subcritical flow depth)

For b = 8 ft (downstream section):

y1 = 0.750 ft (low stage, with a drop)

y2 = 4.964 ft (high stage, without a drop)

For a contraction without a gradual hydraulic drop, the high stages for intermediate sections are computed with the cubic equation.


Fig. 3-6 (Chow)

B. When a gradual hydraulic drop is desired, the downstream flow depth should be at the low flow stage.

Narrow the width in the contraction to force a critical flow condition.

At the point of inflection, the flow is critical.

The critical flow depth is:

yc = (2/3) E = (2/3) (5.062) = 3.375 ft

The critical velocity is:

Vc = (g yc)1/2 = (32.17 × 3.375)1/2 = 10.42 fps

The width of the critical section is:

bc = Q/(Vcyc) = 100/(10.42 × 3.375) = 2.844 ft

The side walls can be drawn as straight lines.

The low and high stages are computed by the cubic equation.

The calculated flow profile is based on the theory of parallel flow.

The flow near the drop is actually curvilinear, and the actual profile would deviate from the theoretical one.

Since at critical flow, the velocity head is one-half of the flow depth:

Vc2/(2g) = yc/2

Q2/(2gAc2) = yc/2

In a rectangular channel:

Q2/(2gbc2yc2) = yc/2

yc = [Q2/(gbc2)]1/3

yc = (q2/g)1/3

Thus, in a rectangular channel, the critical flow depth is a function only of the unit-width discharge.

ONLINE APPLICATION:

With Q = 100 cfs, b1 = 10 ft, and y1= 5 ft, use onlinechannel17.php to find bc = ?


3.6  MOMENTUM IN OPEN-CHANNEL FLOW

  • Energy is a scalar:

    E = ∫ Fdx

  • Momentum is a vector:

    M = ∫ Fdt

  • Energy is:

    E = (1/2) mV2

  • Momentum is:

    M = mV

  • Mass flux is:

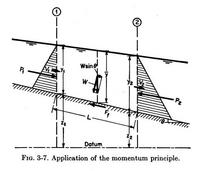
    Mass flux = ρQ

  • Momentum flux (mass flux × velocity = force) is:

    F = ρQV

  • Momentum flux is:

    F = βρQV

  • Newton's Second Law: The rate of change of momentum (momentum flux) is equal to the sum of all external forces (surface and body) acting on the control volume.

    ρQ (β2V2 - β1V1) = P1 - P2 + Wsinθ - Ff


    Fig. 3-7 (Chow)

  • The pressure forces are:

    P1 = (1/2) γy1 (y1 b) = (1/2) γby12

    P2 = (1/2) γy2 (y2 b) = (1/2) γby22

  • The friction force is:

    Ff = γ (hf'/L) bYL = γ hf' bY

    in which hf' is the friction head loss, and Y = (1/2) (y1 + y2) (the average flow depth).

  • The discharge through the reach is:

    Q = (1/2) (V1 + V2) bY

  • The weight of the water in the control volume is:

    W = γbYL

    sinθ = (z1 - z2)/L

    W sinθ = γbY(z1 - z2)

  • Substitution leads to:

    z1 + y1 + β1V12/(2g) = z2 + y2 + β2V22/(2g) + hf'

  • This equation is similar to the energy equation, but it has β instead of α

  • The energy equation measures internal losses.

  • The momentum equation measures external losses.

  • The losses have a tendency to be equal.


3.7  SPECIFIC FORCE

  • Application of the momentum principle to a short horizontal reach of a prismatic channel.

  • In a short reach, the friction can be neglected: Ff = 0.

  • In a horizontal reach, θ = 0; then: Wsinθ = 0.

  • In a wide prismatic channel reach, β = 1.

  • Thus, momentum flux is balanced by the pressure forces only:

    ρQ (V2 - V1) = P1 - P2

  • The pressure forces are:

    P1 = γ z1_barA1

    P2 = γ z2_barA2

    where z1__bar and z2__bar are the distances from the water surface to the centroid of the area, at cross sections 1 and 2, respectively.

  • The velocities are:

    V1 = Q/A1

    V2 = Q/A2

  • Substituting:

    ρQ (Q/A2 - Q/A1) = γ z1_barA1 - γ z2_barA2

  • Rearranging:

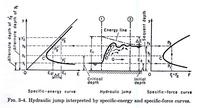
    [Q2/(gA1)] + z1_barA1 = [Q2/(gA2)] + z2_barA2 = constant

  • Therefore, in any cross section in a short horizontal prismatic channel:

    [Q2/(gA)] + z_barA = constant

  • This is a specific force, or force (momentum flux) per weight per unit of volume, with L3 units.

    F = [Q2/(gA)] + z_barA


    Fig. 3-9 (Chow)

  • The minimum specific force is:

    dF/dy = - [Q2/(gA2)] dA/dy + d(z_barA)/dy = 0

  • For a change dy in the depth, the corresponding change d(z_barA) in static moment of the water area about the free surface is:

    d(z_barA) = [A (z_bar + dy) + T dy (dy/2)] - z_barA

  • Neglecting the second-order term:

    d(z_barA) = A dy

    d(z_barA)/dy = A

  • The top width T is:

    T = dA/dy

  • Substituting:

    - [Q2/(gA2)]T + A = 0

    [(Q2T)/(gA3)] = 1

    (V2T)/(gA) = 1

    F2 = 1

    F = 1


    Fig. 3-9 (Chow)

  • The specific force is:

    F = [Q2/(gA)] + z_barA = constant

    		   [L3]

  • The specific force for a wide rectangular channel:

    (q2b2)/(gby) + (y/2)yb = constant

    		   [L3]

    q2/(gy) + (1/2)y2 = constant

    		   [L2]

    (v2y)/g + (1/2)y2 = constant

    		   [L2]

  • In units of force, the specific force is:

    F = γ [Q2/(gA)] + γ z_barA = constant

    		   [F]

    γ (q2b2)/(gby) + γ (y/2)yb = constant

    		   [F]

    γ q2/(gy) + (1/2) γ y2 = constant

    		   [F L-1]

    γ (v2y)/g + (1/2) γ y2 = constant

    		   [F L-1]

 

 
100915