CIV E 530 - OPEN-CHANNEL HYDRAULICS SPRING 2003 - HOMEWORK 11 - SOLUTION

PROBLEM 1

Verify that:

h_j/ E₁ = [(1 + 8F1²)^1/2 - 3] / [ F₁² + 2]

Solution:

h_j/ E₁ = (y₂ - y₁) / E₁

E₁ = y₁ + v₁²/(2g)

E₁ = y₁ (1 + F₁²/2)

E₁ = (y₁/2) (2 + F₁²)

h_j/ E₁ = (y₂ - y₁) / [(y₁/2) (2 + F₁²)]

h_j/ E₁ = [2 (y₂/y₁) - 2] / (F₁² + 2)

h_j/ E₁ = [(1 + 8F₁²)^1/2 - 1 - 2] / (F₁² + 2)

h_j/ E₁ = [(1 + 8F₁²)^1/2 - 3] / (F₁² + 2)   ANSWER.

PROBLEM 2

b= 20 ft

z = 0.

n= 0.03

S_o = 0.04

y₁ = 3 ft.

Find

(a) discharge Q

(b) jump height h_j

(c) energy loss ΔE

(d) efficiency E₂/E₁ and

(e) the distance L of the jump from the dam.

Solution:

v₁= (1.486/n) R^2/3 S^1/2

v₁= (1.486/0.03) [(20×3)/(20 + 2×3)]^2/3 (0.04)^1/2

v₁= 17.3 fps.

F₁= v₁/(g y₁) ^1/2

F₁= 17.3/(32.17 × 3.0) ^1/2

F₁= 1.76

The flow is supercritical upstream. A hydraulic jump will occur in the channel.

(a)

Q = v₁ y₁ b

Q = 17.3 × 3.0 × 20.0 = 1038 cfs.   ANSWER.

(b)

E₁ = y₁ + v₁²/(2g)

E₁ = y₁ (1 + F₁²/2)

E₁ = 3.0 [1 + (1.76)²/2]

E₁ = 7.65

h_j = E₁ [(1 + 8F₁²)^1/2 - 3]/[F₁² + 2]

h_j = 7.65 [(1 + 8 × 1.76²)^1/2 - 3]/[1.76² + 2]

h_j = 3.12 ft.   ANSWER.

(c)

y₂ = (1/2) y₁ [(1 + 8F₁²)^1/2 - 1]

y₂ = (1/2) 3.0 [(1 + 8 × 1.76²) ^1/2 - 1]

y₂ = 6.12 ft.

ΔE = (y₂ - y₁)³/(4y₂y₁)

ΔE = (6.12 - 3.0)³/(4 × 6.12 × 3.0)

ΔE = 0.414 ft.   ANSWER.

(d)

E₂/E₁ = [(8F₁² + 1)^3/2 - 4F₁² + 1] / [8F₁² (2 + F₁²)]

E₂/E₁ = [(8 × 1.76² + 1)^3/2 - 4 × 1.76² + 1] / [8 × 1.76² (2 + 1.76²)

E₂/E₁ = 0.946   ANSWER.

(e)

L = [(y_d - y₁) - h_j] / S_o

L = [(7.0 - 3.0) - 3.12] / 0.04

L = [4.0 - 3.12] / 0.04

L = 22 ft.   ANSWER.  

PROBLEM 3

b= wide rectangular (assume b = 1000 ft).

z = 0.

n= 0.025

S_{o (up)} = 0.01

S_{o (tw)} = 0.002

y_(tw) = 5 ft.

Find the location of the hydraulic jump.

Solution:

q = (1.486/n) y_(tw)^5/3 S_o^1/2

q = (1.486/0.025) 5^5/3 0.002^1/2

q = 38.86 cfs/ft

Assume b = 1000 ft.

Q = 3886 cfs.

z = 0.

S_o = 0.01

n = 0.025

Use CHANNEL to calculate

y₁ = 3.093 ft.

v₁ = 12.565 fps.

F₁ = 1.26

y₂ = (1/2) y₁ [(1 + 8F₁²)^1/2 - 1]

y₂ = (1/2) (3.093) [(1 + 8 × 1.26²)^1/2 - 1]

y₂ = 4.18 ft.

Since y_(tw) = 5 > 4.18 = y₂, the hydraulic jump will occur u/s of the change in slope.   ANSWER.

PROBLEM 4

b= 30 ft

Q = 300 cfs

ΔE = 5 ft.

Find y₁ and y₂.

Solution:

q = 300 / 30 = 10 cfs/ft.

ΔE = [(y₂ - y₁)³]/(4y₁y₂)

ΔE = y₁³ [(y₂/y₁) - 1]³/(4y₁y₂)

ΔE = [(y₂/y₁) - 1]³ y₁ /(4y₂/y₁)

y₁ = 4 ΔE (y₂/y₁) / [(y₂/y₁) - 1]³       (Eq. 1)

y₂/y₁ = (1/2) [(1 + 8F1²)^1/2 - 1]       (Eq. 2)

v₁ = q/y₁       (Eq. 3)

F₁ = v₁/(gy₁)^1/2       (Eq. 4)

Procedure:

Assume F₁, use Eq. 2 to calculate y₂/y₁; then use Eq. 1 to calculate y₁; then use Eq. 3 to calculate v₁; then use Eq. 4 to calculate F₁; stop if calculated F₁ is close to assumed one.

y₁ = 0.434 ft.   ANSWER.

y₂ = (y₂/y₁) y₁ = 8.240 × 0.434 = 3.576 ft.   ANSWER.

ΔE = [(y₂ - y₁)³]/(4y₁y₂) = (3.576 - 0.434)³/(4 × 3.576 × 0.434) = 4.996 ≅ 5.     OK.

 

PROBLEM 5

Rectangular stilling basin.

v = 80 fps.

z = 0.

y₁ = 6 ft.

Find:

(a) the sequent tailwater depth

(b) the length of the basin required to confine the jump

(c) the efficiency of the jump

(d) the type of jump.

Solution:

F₁ = v₁/(gy₁)^1/2

F₁ = 80/(32.17 × 6.0)^1/2

F₁ = 5.76

(a)

y₂ = (1/2) y₁ [(1 + 8F1²)^1/2 - 1]

y₂ = 45.96 ft.   ANSWER.

(b)

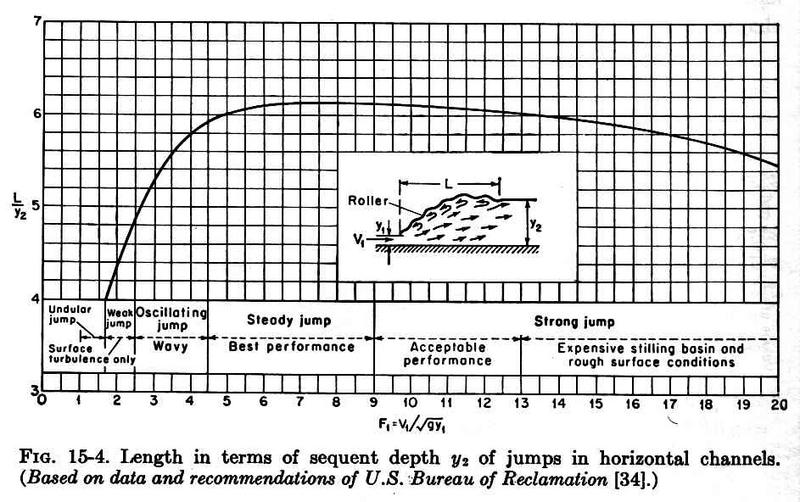
For F₁ = 5.76, L/y₂ = 6.1 (Fig. 15.4 Chow)

 

 

L = 6.1 × 45.96 = 280 ft.   ANSWER.

(c)

E₂/E₁ = [(8F₁² + 1)^3/2 - 4F₁² + 1] / [8F₁² (2 + F₁²)]

E₂/E₁ = 0.45   ANSWER.

(d)

For F₁ = 5.76, the type of jump is steady.   ANSWER.

040503