• The storage concept is well established in flow-routing theory and practice.

• Storage routing is used in reservoir, stream channel, and catchment routing.

• Techniques for storage routing are based on the differential equation of storage.

• The partial differential equation of water continuity is:

  ∂Q/∂x + ∂A/∂t = 0

  which states that in a control volume, the gradient of discharge should be balanced by the rate-of-rise of flow area.

• The differential equation of storage is obtained by lumping spatial variations:

  ΔQ/Δx + ΔA/Δt = 0

• With ΔQ = O - I, and ΔS = ΔA Δx, leads to:

  I - O = ΔS/Δt

• In differential form:

  I - O = dS/dt

• Within a time step, any difference between inflow and outflow is balanced by the change in storage.

• The inflow hydrograph (boundary conditions), initial conditions, reservoir characteristics, and operational rules are known.

• The objective of reservoir routing is to calculate the outflow hydrograph.

  Storage-Outflow Relations

• In an ideal reservoir, storage is a function of outflow only.

• The general relationship between outflow and storage is:

  S = f(O)

• A common relationship between outflow and storage is:

  S = KOn

• Figure 8-1.

• For n = 1, we get the linear reservoir:

  S = KO

• The linear reservoir equation is applicable to simulated routing.

• The nonlinear reservoir equation is applicable to actual routing.

• Exception: Spillway in Colorado, where a linear reservoir was actually built!

• In linear reservoir routing, the constant K represents the amount of storage or diffusion.

• Greater values of K result in increased outflow hydrograph diffusion.

• For actual reservoirs and spillways, the nonlinear properties of the storage-outflow relations must be determined in advance.

• Outflow will depend on whether the flow is discharged through either closed conduit(s), overflow spillway(s), or a combination of the two.

• A general outflow formula is the following:

  O = Cd Z Hy

• Z represents either the cross-sectional area in close conduits, or the length of the crest in an overflow spillway.

• C_d is the discharge coefficient; H is the hydraulic head; y is the rating exponent.

• Theoretical values of C_d and y are determined using hydraulic principles.

• For the free-outlet closed conduit, the conservation of energy between reservoir pool and outlet elevations, neglecting entrance and friction losses, leads to:

  H = V2 /(2g)

• Therefore, the outflow is:

  O = V A = (2gH)1/2 Z

• It follows that y = 1/2 and C_d = 4.43 in SI units and 8.02 in U.S. customary units.

• These theoretical values are reduced by about 30% to account for flow contraction and entrance losses.

• For an ungated overflow spillway, the critical flow condition [flow depth y = (2/3) H] in the vicinity of the crest leads to:

  O = V A = [g (2/3)H)1/2 [(2/3)H] Z

  which reduces to:

  O = (2/3) [(2/3)g] 1/2 Z H 3/2

• It follows that y = 3/2 and C_d = 1.7 in SI units and 3.09 in U.S. customary units.

• In practice, the discharge coefficient of an overflow spillway is not constant, varying with H between 85 and 130% of the theoretical value (that assumes critical flow in the vicinity of the crest).

• In the proportional (or linear reservoir) overflow spillway (weir), the cross-sectional flow area grows in proportion to the half-power of H.

• Therefore, outflow is linearly related to H, and a linear storage-outflow rating is applicable.

• Spillway Photos.

• The differential equation of storage can be solved by analytical or numerical means.

• The numerical approach is preferred because it can take an arbitrary inflow hydrograph and can be solved with the computer.

• The solution is accomplished by discretization on the x-t plane.

• The discretization leads to:

  (I1 + I2) / 2 - (O1 + O2) / 2 = (S2 - S1) / Δt

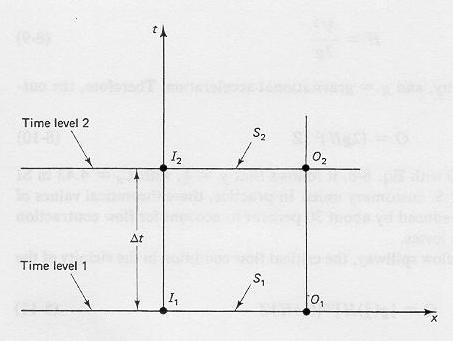
  Fig. 8-2

• At each time level, the linear reservoir storage-outflow relation is satisfied:

  S1 = KO1

  S2 = KO2

• Substituting these equations into the discretized differential equation of storage:

  O2 = C0I2 + C1I1 + C2O1

• in which the routing coefficients are defined as follows:

  C0 = (Δt/K) / [2 + (Δt/K)]

  C1 = C0

  C2 = [2 - (Δt/K)] / [2 + (Δt/K)]

• Since C₀ + C₁ + C₂ = 1, the routing coefficients are interpreted as weighting coefficients.

• These coefficients are a function of Δt/K.

• Values of routing coefficients as a function of Δt/K are shown in Table 8-1.

• Example 8-1.

• Example 8-1 Graph.

• The peak flow is attenuated and the time base increased.

• In the linear reservoir case, the amount of attenuation is a function of Δt/K.

• The smaller this ratio, the greater the amount of attenuation exerted by the reservoir.

• Values of Δt/K greater than 2 can lead to negative outflows; this should be avoided.

• Peak outflow occurs at the time when inflow equals outflow; see Example 8-1 Graph.

• Since outflow is proportional to storage, peak outflow corresponds to peak (or maximum) storage.

• Peak storage occurs when outflow equals inflow; after this, outflow is drawing from storage.

• Therefore, peak outflow occurs when outflow equals inflow.

• Reservoir routing has an immediate outflow response, see Example 8-1 Graph.

• There is no lag between the start of inflow and the start of outflow.

• This property is due to the fact that in an ideal reservoir, with water surface slope equal to zero, surface water have an infinite velocity of propagation.

  c = u + (gd)1/2

  c/u = 1 + (gd)1/2/u

  c/u = 1 + 1/F

• In other words, when the Froude number is zero (u = 0), the celerity of surface waves is infinity.

• The storage indication method is used to route flood waves through actual reservoirs.

• The storage indication method is also known as the Modified Puls method.

• The method is based on the discretization of the differential equation of storage.

  I - O = dS/dt

• Discretization on the x-t plane leads to:

  (I1 + I2) / 2 - (O1 + O2) / 2 = (S2 - S1) / Δt

• Putting all unknowns in the LHS:

  (2S2/Δt) + O2 = I1 + I2 + (2S1/Δt) - O1

• The LHS is known as the storage-indication quantity.  

   

• It is first necessary to assemble geometric and hydraulic reservoir data in suitable form.

• For this purpose, the following curves (or tables) are prepared:
  
  
  1. Elevation-storage: obtained from the geometry (topography and bathymetry) of the reservoir.

  2. Elevation-outflow: obtained from the hydraulic properties of the spillway (weir or closed-conduit spillway)

  3. Storage-outflow: obtained from the first two curves (for the same elevation, the corresponding storage and outflow).

  4. Storage indication-outflow: obtained from the storage-outflow relation [for each pair of storage-outflow, create a storage indication (2S/Δt + O) and plot this quantity vs outflow].

• The time interval Δt is selected to linearize the inflow hydrograph.

• It should be at least 1/5 of the time-of-rise of the inflow hydrograph.  

   

• Application of the storage-indication method consists of a recursive procedure:
  
  
  1. Set the counter n = 1 to start.

  2. Use the discretized storage-indication equation to calculate the storage indication quantity (2S/Δt + O) at time level n+1:

     (2S_n+1/Δt + O_n+1)

  3. With (2S_n+1/Δt + O_n+1), use the storage-indication vs outflow relation to calculate O_n+1.

  4. With (2S_n+1/Δt + O_n+1) and O_n+1, calculate:

     (2S_n+1/Δt - O_n+1).

  5. Increment the counter by 1, and go back to step 2 and repeat.

• The procedure is illustrated by Example 8-2 and Table 8-3.

• The results of Table 8-3 Column 5 are the same as those of Table 8-2 Column 6.

• This confirms that a linear reservoir can be also routed with the storage-indication method.  

   

• The application of the storage-indication method to an actual reservoir (Turner reservoir, San Diego North County) is shown by Example 8-3

• Example 8-3: Table 8-4

• Example 8-3: Figure 8-4

• Example 8-3: Table 8-5

  Spillway of Turner reservoir, San Diego County.

Go to Chapter 9A.