CIV E 445 - APPLIED HYDROLOGY SPRING 2014 HOMEWORK No. 5 SOLUTION Since rainfall duration is greater than time of concentration, the flow is superconcentrated and the entire catchment is contributing. For subcatchments with different runoff coefficients, use a weighted formula for peak runoff (see Eq. 4-14): Qp = I Σ(CA) Qp = 55 mm/h × [ (0.3 × 175 × 30/100) + (0.5 × 175 × 40/100) + (0.9 × 175 × 30/100) ] ha × (10,000 m2/ha × 0.001 m/mm) / (3600 s/h) = Qp = 14.97 m3/s.   ANSWER. Several rainfall durations are tried, as shown in the following table. tr (min) I (mm/h) Subarea A (C = 0.9) (ha) Subarea B (C = 0.3) (ha) Σ(CA) Qp (m3/s) 20 147.7 66 51.33 74.8 30.68 30 123.9 66 77 82.5 28.4 40 107.5 66 102.67 90.2 26.95 50 95.5 66 128.33 97.9 25.96 60 86.1 66 154 105.6 25.26 The fraction of subarea B contributing to peak runoff increases linearly with rainfall duration. Therefore: Qp = I Σ(CA), in m3/s. The 50-y peak runoff is the maximum value, corresponding to a 60-min duration: 30.68 m3/s.  ANSWER. Using Eq. 4-19, the equilibrium outflow is: qe = iL / 3600 = (40 mm/h × 100 m × 0.001 m/mm × 1000 Liters/m3) / (3600 s/h) = qe = 1.11 Liters/s/m = 1.11 × 10-3 m3/s/m = 0.00111 m2/s. For T = 20°C, ν = 1.0 × 10-6 m2/s (Table A-1). Using Eq. 4-27: CL = (9.81 m/s2 × 0.015) / (3 × 1.0 × 10-6 m2/s) = 49,050 m-1s-1. In Eq. 4-25, for laminar flow, b = CL, and m = 3. Therefore: he = (qe / CL)1/3 = (0.00111/49,050)1/3 = 0.00283 m = 2.83 mm.  ANSWER. For T = 30°C, ν = 0.801 × 10-6 m2/s. Using Eq. 4-27: CL = 61,236 m-1s-1. Therefore: he = (qe / CL)1/3 = (0.00111/61,236)1/3 = 0.00263 m = 2.63 mm.  ANSWER. The rainfall excess in m/s is: i = (25 mm/h × 0.001 m/mm) / (3600 s/h) = 6.94×10-6 m/s. qe = 6.94×10-6 m/s × 80 m = 0.0005555 m3/s/m = 0.5555 L/s/m. For 75% turbulent flow, m = 2. Therefore, in Eq. 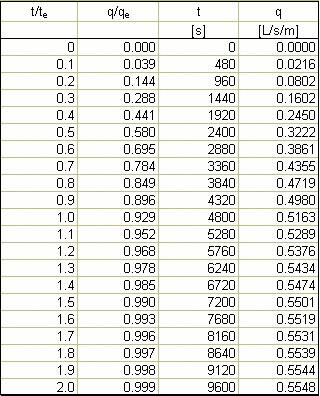4-29: te = [ 2 × (0.05 × 80)1 / 2 ] / [(6.94×10-6)1 / 2 × 0.011 / 4] = 4800 s. Using Eq. 4-36, the rising limb of the overland flow hydrograph is calculated as shown in the following table.  ANSWER.