Problem 12-1
The total rainfall depth is: P = 16 cm. With CN = 81, and R = 2.54 cm/in, the effective rainfall depth (i.e., runoff) (Eq. 5-9) is: Q = 10.56 cm.
Assuming φ between 0 and 1 cm/h: [(1 - φ) • 1 + (2 - φ) • 1 + (5 - φ) • 1 + (4 - φ) • 1 + (3 - φ) • 1 + (1 - φ) • 1] = 10.56.
From which: φ = 0.907 cm/h. The total and effective rainfall pattern is:
The accumulated effective rainfall depth is: 10.56 cm.
The total runoff volume is:
85 km2 • 10.56 cm = 897.6 km2-cm = 8.976 hm3.
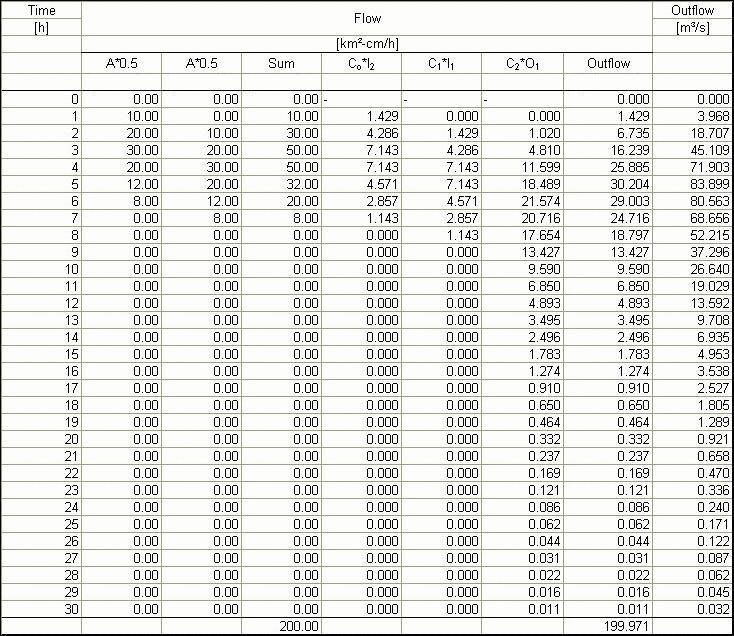
The calculations are shown in the following table:
The sum of outflow hydrograph ordinates is 897.6 km2-cm/h.
The integration of the outflow hydrograph results in:
897.6 km2-cm/h • 1 h = 897.6 km2-cm = 8.976 hm3, which is the same as the total runoff volume.
The same results obtained with ONLINE ROUTING 06.
ANSWER.
Problem 12-2
Since Δt = 1 h, and K = 3 h: Δt /K = 1/3, and from Eq. 8-16 to 8-18, the linear reservoir-routing coefficients are the following:
C0 = 1/7; C1 = 1/7; C2 = 5/7.
The unit runoff volume is: (20+40+60+40+24+16) km2 • 1 cm = 200 km2-cm = 2 hm3.
Since the duration of the SI unit hydrograph (1 cm of runoff) is 2 h, the rainfall intensity is 0.50 cm/h.
The same results obtained with ONLINE ROUTING 07. ANSWER.
Problem 12-3
For K = 12 hr, and N = 4, the peak flow is 723.115 m3/s at 48 hours. ANSWER.
For K = 18 hr, and N = 5, the peak flow is 429.853 m3/s at 84 hours. ANSWER.
Problem 12-4
The time of concentration is tc = 6 h.
The effective rainfall duration is tr = 1 h.
Therefore, the time base of the translated-only hydrograph Tb = tc + tr = 6 + 1 = 7 h.
K can be based on Eq. 10-4, using two consecutive hydrograph ordinates after 7 h.
For the ordinates at 7 h and 8 h:
K = - [(47 + 28) / 2] / [28 - 47) / 1] = 1.97 h
Since this is a hydrograph derived from measured data, it is appropriate to average several values of K computed
at the tail of the hydrograph. For 8 h and 9 h: K = 2.04 h.
For 9 h and 10 h: K = 1.92 h. For 10 h and 11 h: K = 2.0 h. The average of four calculations is K = 1.98 h, say K = 2 h.