CIV E 445 - APPLIED HYDROLOGY
SPRING 2011
SOLUTION TO HOMEWORK 6, CHAPTER 5

Problem 6-1

Running online curve number: Q = 5.25 in.

Problem 6-2

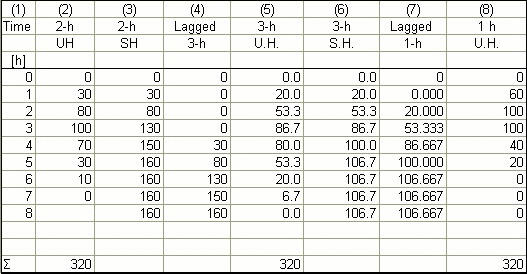
The 3-h unit hydrograph is shown in Col. 5; the 1-h unit hydrograph is shown in Col. 8. The sum of Cols. 2, 5, and 8 is the same.  The output from online S-hydrograph verifies spreadsheet or hand calculations. ANSWER.

Problem 6-3

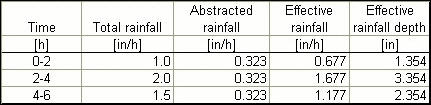
The total rainfall in the 6-h period is: P = 9 in. With runoff curve number CN = 84 and total rainfall P = 9 in., use Eq. 5-8 to calculate the direct runoff Q: Q = 7.06 in. Assume φ-index between 0 and 1.0 in./h. Therefore: [ (1.0 - φ) • 2 h + (2.0 - φ) • 2 h + (1.5 - φ) • 2 h ] = 7.06 in. Solving for φ: φ = 0.323 in/h. Rainfall intensities and depths are as follows.

The unit hydrograph is convoluted with the effective rainfall depth pattern as shown in the following table.

To verify that the composite-hydrograph ordinates are correct, the radio of sums ( 3178 / 450 = 7.06) should be equal to the sum of the effective rainfall depth: (1.354 + 3.354 + 2.354) = 7.06. The composite hydrograph for the effective storm pattern is shown in Col. 6. The output from online Convolution verifies hand calculations. ANSWER.

Problem 6-4

To convolute the 2-h unit hydrograph with the effective storm pattern defined at intervals of 3 h, it is necessary to change the unit hydrograph duration to 3 h. Then, we convolute the 3-h unit hydrohgraph with the effective storm pattern. The change in unit hydrograph duration and unit hydrograph convolution are shown in the following table. The same results are obtained with online programs S-hydrograph and Convolution. In the latter, use CN = 100, because effective rainfall was given.