SPRING 2010
SOLUTIONS TO HOMEWORK 11 , CHAPTER 9
Problem 11-1
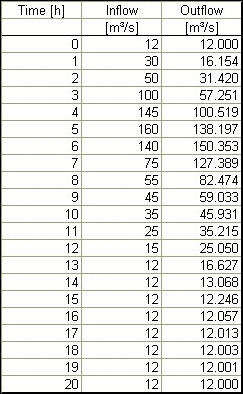
Using Eqs. 9-4 to 9-6, the Muskingum routing coefficients are the following:
C0 = 0.231, C1 = 0.538, C2 = 0.231
The peak outflow is 150.353 m3/s, and it occurs at 6 h. The same answer is obtained with ONLINE ROUTING 04. ANSWER.
Problem 11-2
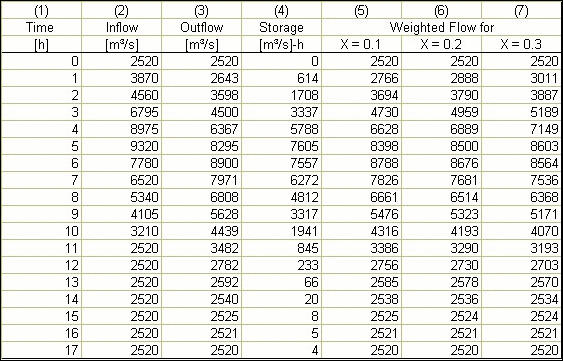
Storage is calculated with Eq. 9-7. Weighted flow is:
[X • I + (1 - X) • O]. The results of the computation are shown in the following table.
The storage (Col. 4) vs. weighed flow relations (Col. 5 to 7) are plotted as shown in Fig. 9-4 of the text. The chosen value of X is that corresponding to the narrowest loop in the storage-weighted flow relation. In this case: X = 0.3. The value of the storage constant K is the slope of the storage-weighted flow relation for X = 0.3: K = 1.25 h. ANSWER.
Problem 11-3
A rough estimate of the discharge at point 5 km upstream can be obtained by discretizing the equation of continuity, Eq. 9-9, using an off-centered numerical scheme:
(Q2 - Q1) / Δx + (A2 - A1) / Δt = 0
in which Q = discharge, A = flow area, Δt = time interval, and Δx = space interval (reach length).
Since the channel width is constant, the change is flow area per time interval is: ΔA = B Δy, in which B = channel width, and Δy = change in stage per time interval. Then :
(Q2 - Q1) / Δx + B (Δy / Δt) = 0
Solving for the upstream discharge (Q1):
Q1 = Q2 + B Δx (Δy / Δt)
Q1 = 1250 + [600 m • 15 km • 1000 m/km • ( 3 mm • 0.001 m/mm) / (3600 s)] = 1257.5 m3/s. ANSWER.
Problem 11-4
The results are summarized in the following table.
The peak outflow is 1,093.39 m3/s, and it occurs at 8 h.
The same answer is obtained with ONLINE ROUTING 05. ANSWER.