Problem 5-2

Several rainfall durations are tried, as shown in the following table.

tr (min)	I (mm/h)	Subarea A (C = 0.8) (ha)	Subarea B (C = 0.3) (ha)	Σ(CA) (ha)	Qp (m3/s)
10	141.73	30	15	28.5	11.22
20	120.35	30	30	33.0	11.03
30	105.42	30	45	37.5	10.98
40	94.31	30	60	42.0	11.00
50	85.67	30	75	46.5	11.06
60	78.74	30	90	51.0	11.15

The fraction of subarea B contributing to peak runoff increases linearly with rainfall duration.

Therefore: Q_p = 0.0027778 I Σ(CA).

The 25-y peak runoff is the maximum value, corresponding to a 10-min duration: 11.22 m³/s.  ANSWER.

Problem 5-3

Using Eq. 4-19, the equilibrium outflow is:

q_e = iL/3600 = (50 mm/h • 144 m • 0.001 m/mm • 1000 L/m³) / (3600 s/h) =

q_e = 2 L/s/m = 2 • 10^-3 m³/s/m = 0.002 m²/s.

For T = 20°C, ν = 1.0 • 10^-6 m²/s (Table A-1).

Using Eq. 4-27: C_L = (9.81 m/s² • 0.01) / (3 • 1.0 • 10^-6 m²/s) = 32,700 m^-1s^-1.

In Eq. 4-25, for laminar flow, b = C_L, and m = 3. Therefore:

h_e = (q_e / C_L)^1/3 = (0.002/32,700)^1/3 = 0.00394 m = 3.94 mm  ANSWER.

For T = 25°C, ν = 0.893 • 10^-6 m²/s.

Using Eq. 4-27: C_L = 36,618 m^-1s^-1.

Therefore, with Eq. 4-25: h_e = (0.002/36,618)^1/3 = 0.00379 m = 3.79 mm  ANSWER.

Problem 5-4

The rainfall excess in m/s is:

i = (25 mm/h • 0.001 m/mm) / (3600 s/h) = 6.94 •10^-6 m/s.

q_e = 6.94 •10^-6 m/s • 80 m = 0.0005555 m³/s/m = 0.5555 L/s/m.

For 75% turbulent flow, m = 2. Therefore, in Eq. 4-29:

t_e = [ 2 • (0.05 • 80)^1/2 ] / [(6.94 •10^-6)^1/2 • 0.01^1/4 ] = 4800 s.

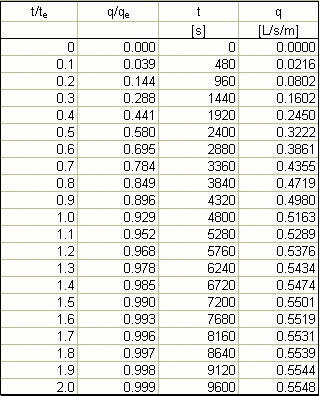
Using Eq. 4-36, the rising limb of the overland flow hydrograph is calculated as shown in the following table.  ANSWER.