APPENDIX B: DERIVATION OF THE NUMERICAL DIFFUSION COEFFICIENT
OF THE MUSKINGUM-CUNGE METHOD
|
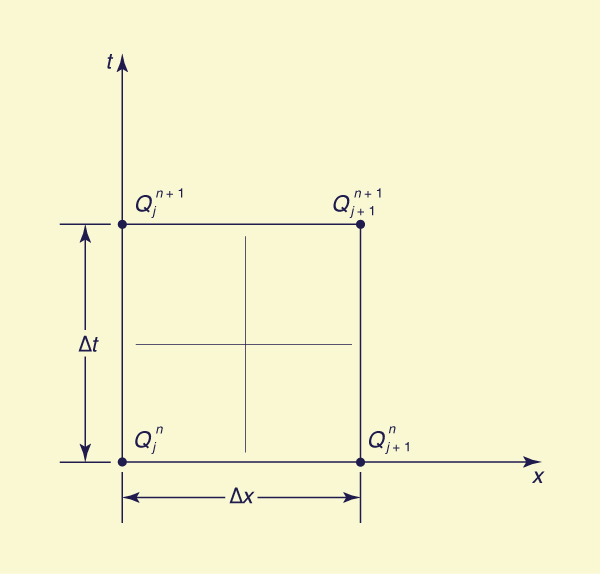
Figure B-1 Space-time discretization of kinematic wave equation.
|
Expanding the grid function Q( jΔx,nΔt ) (Fig. B-1) in Taylor series about point
( jΔx,nΔt ) leads to:
∂Q
1 ∂2Q
Q j n+1 =
Q j n + [ _____ ] j Δt + ___ [ ______ ] j Δt 2 + o (Δt 3)
∂t
2 ∂t 2
| (B.1) |
∂Q
1 ∂2Q
Q j+1n+1 =
Q j+1 n + [ _____ ] j+1 Δt + ___ [ ______ ] j+1 Δt 2 + o (Δt 3)
∂t
2 ∂t 2
| (B.2) |
∂Q
1 ∂2Q
Q j+1n =
Q j n + [ _____ ] n Δx + ___ [ ______ ] n Δx 2 + o (Δx 3)
∂x
2 ∂x 2
| (B.3) |
∂Q
1 ∂2Q
Q j+1n+1 =
Q j n+1 + [ _____ ] n+1 Δx + ___ [ ______ ] n+1 Δx 2 + o (Δx 3)
∂x
2 ∂x 2
| (B.4) |
Substituting Eqs. B.1 to B.4 into Eq. 9-61 and neglecting third-order terms yields:
∂Q
1
∂2Q
X
{ [ ____ ] j
Δt +
____
[ ______ ] j Δt 2
}
∂t
2
∂t 2
| |
∂Q
1
∂2Q
+ (1 - X )
{ [ _____ ] j+1
Δt +
____
[ _____ ] j+1 Δt 2
}
∂t
2
∂t 2
| |
C
∂Q
1
∂2Q
+ ____
{ [ _____ ] n
Δx +
____
[ ______ ] n Δx 2
}
2
∂x
2
∂x 2
| |
C
∂Q
1
∂2Q
+ ____
{ [ _____ ] n+1
Δx +
____
[ ______ ] n+1 Δx 2
} = 0
2
∂x
2
∂x 2
| (B.5) |
in which C = c (Δt /Δx) is the Courant number.
Expressing the derivatives at grid point [( j + 1)Δx, (n + 1)Δt ] in terms of the derivatives at grid point ( jΔx, nΔt ) by means of Taylor series:
∂Q
∂Q
∂2Q
[ _____ ] j+1 =
[ _____ ] j + [ ______ ] j,n Δx + o (Δx 2)
∂t
∂t
∂x ∂t
| (B.6) |
∂Q
∂Q
∂2Q
[ _____ ] n+1 =
[ _____ ] n + [ _______ ] j,n Δt + o (Δt 2)
∂x
∂x
∂x ∂t
| (B.7) |
∂2Q
∂2Q
∂3Q
[ ______ ] j+1 =
[ ______ ] j + [ _______ ] j Δx + o (Δx
2)
∂t 2
∂t 2
∂t 2∂x
| (B.8) |
∂2Q
∂2Q
∂3Q
[ ______ ] n+1 =
[ ______ ] n + [ _______ ] n Δt + o (Δt 2)
∂x 2
∂x 2
∂x 2∂t
| (B.9) |
Substituting Eqs. B.6 to B.9 into B.5 and neglecting third-order terms:
∂Q
1
∂2Q
X
{ [ _____ ] j
Δt +
____
[ ______ ] j Δt 2
}
∂t
2
∂t 2
| |
∂Q
∂2Q
1
∂2Q
+ (1 - X )
{ [ _____ ] j
Δt +
[ ______ ] j,n Δx Δt +
____
[ ______ ] j Δt 2
}
∂t
∂x ∂t
2
∂t 2
| |
C
∂Q
1
∂2Q
+ ____
{ [ _____ ] n
Δx +
____
[ ______ ] n Δx 2
}
2
∂x
2
∂x 2
| |
C
∂Q
∂2Q
1
∂2Q
+ ____
{ [ _____ ] n
Δx +
[ ______ ] j,n Δx Δt +
____
[ ______ ] n Δx 2
} = 0
2
∂x
∂x ∂t
2
∂x 2
| (B.10) |
In Eq. B.10, dividing by Δt and simplifying:
∂Q
∂Q
Δt
∂2Q
c Δx
∂2Q
[ _____ ] j +
c [ _____ ] n + ____ [ ______ ] j + ______ [ ______ ] n
∂t
∂x
2
∂t 2
2
∂x 2
| |
C
∂2Q
+ Δx
{ ( 1 - X ) + ____ }
[ ______ ] j,n
= 0
2
∂x ∂t
| (B.11) |
The first two terms of Eq. B.11 constitute the kinematic wave equation, Eq. 9-18. The remaining terms are the error R of the first-order-accurate numerical scheme:
Δt
∂2Q
c Δx
∂2Q
C
∂2Q
R = ____ [ ______ ] j + ______ [ ______ ] n + Δx
{ ( 1 - X ) + _____ }
[ ______ ] j,n
= 0
2
∂t 2
2
∂x 2
2
∂x ∂t
| (B.12) |
From Eq. 9-18:
∂Q
∂Q
____ = - c ____
∂t
∂x
| (B.13) |
Therefore:
∂2Q
∂2Q
______ = - c ______
∂x ∂t
∂x 2
| (B.14) |
∂2Q
∂2Q
______ = c 2 ______
∂t 2
∂x 2
| (B.15) |
Substituting Eqs. B.14 and B.15 into B.12 and simplifying:
1 ∂2Q
R = c Δx ( X - ___ ) _____
2 ∂x 2
| (B.16) |
Comparing Eq. B.16 with the right-hand side of the diffusion wave equation, repeated here:
∂Q
∂Q
∂2Q
____ + c _____ = νh _______
∂t
∂x
∂x 2
| (B.17) |
it follows that the numerical diffusion coefficient of the Muskingum-Cunge method is:
1
νh = c Δx ( ___ - X )
2
| (B.18) |
|