|
|
|
CHAPTER 11: UNSTEADY RAPIDLY VARIED FLOW |
11.1 SURFACE WAVES
|
|
Surface waves are unsteady open-channel flow features typically occurring under high Froude-number flows.
Figure 11-1 shows a surface wave on the Hassayampa river,
near Morristown, Arizona (Phillips and Ingersoll, 1998).
The disturbance is a wave propagating slowly downstream, and it is indicative of
hydraulic characteristics in alluvial channels under upper-regime flow conditions
|
|
Figure 11-3 shows the Santa Catarina river, at Monterrey, Nuevo Leon, Mexico, during the passage of Hurricane Gilbert, on September 17, 1988. The observed large surface waves are an indication of the high Froude-number flows which most likely prevailed during the passage of the flood.
|
11.2 SURGES
|
|
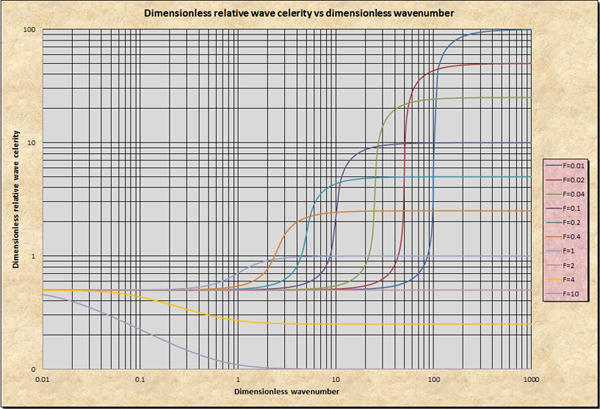
Surges are perturbations created by sudden gate closures or rapid changes in stage or flow depth. Typically, a surge does not attenuate readily, traveling along the channel for a considerable distance. Surges are avoided by opening gates slowly, to minimize the possibility of sudden stage or depth changes. Surge attenuation increases as the dimensionless wavenumber decreases from that corresponding to a true dynamic wave (with constant celerity, i.e, to the right side of the wavenumber spectrum) to that corresponding to a mixed dynamic wave (with variable celerity, i.e., along the upper falling side of the S-curve) (Fig. 11-4).
|
Based on the above criterion, a first approximation to the time of opening To of a canal gate, to avoid a surge, is (Ponce et al., 1999):
|
k uo To ≥ _______ g So | (11-1) |
in which uo = flow velocity, So = channel slope, g = gravitational acceleration, and k = a constant varying with Froude number as shown in Table 11-1.
| ||||||||||||||
11.3 KINEMATIC SHOCKS
|
|
Kinematic shocks are kinematic waves that have steepened to the point where they become, for all practical purposes, a wall of water, with a near vertical face. Actually, the shock is not a perfect discontinuity; however, its thickness is relatively small compared to the wavelength of the disturbance (Lighthill and Whitham, 1955).
Kinematic waves travel downstream, and may either steepen or flatten out, depending on their interaction with the cross-sectional geometry. Only kinematic waves that steepen can develop into kinematic shocks. While kinematic waves are gradually varied, kinematic shocks are rapidly varied.
The development of a kinematic shock is a function of the following flow conditions (Ponce and Windingland, 1985):
The type of wave
The more kinematic a wave is (the smaller the dimensionless wavenumber), the less its tendency to attenuate and, therefore, the more its tendency to steepen.
The amount of baseflow
The smaller the base-to-peak flow ratio, the greater the tendency for the wave to steepen. This is due to wave nonlinearities (inbank larger flows travel with greater celerities).
The flow regime
High-Froude number flows have less tendency to attenuate disturbances; therefore, the higher the Froude number, the lesser the attenuation. In the limit, as the flow approaches the Vedernikov number V = 1 (i.e., F = 2 for Chezy friction in hydraulically wide channels), the flow becomes neutrally stable and attenuation is reduced to zero.
The type of cross section
Hydraulically wide channels, for which the rating exponent β = 1.5 (Chezy friction), have a greater tendency to steepen that triangular channels, for which β = 1.25. Inherently stable channels, for which β = 1, have no tendency to steepen (See Table 10-3 for other applicable values of β).
Thus, kinematic shocks will develop in field situations involving: (a) a kinematic wave, (b) an ephemeral channel (zero baseflow), (c) a high flow rate (a flood), and (d) a hydraulically wide channel. This may be the case of a major cloudburst rapidly concentrating flow through a canyon in a semiarid region.
A well-documented flash flood, which was in all probability a kinematic shock, occurred July 26, 1981 in Tanque Verde Creek, a tributary of the Santa Cruz river, in eastern Arizona. The flood, which killed eight people, was, by all accounts, only a 2-yr flood. However, the suddenness of the flood which, according to survivors' reports amounted to a "wall of water," resulted in substantial loss of life (Hjalmarson, 1984).
Kinematic shocks have been observed with certain frequency in laboratory overland flow computations. These computations are known to be conducive to kinematic shock development (Kibler and Woolhiser, 1970). The shock presence is attributed to the prescribed spatial regularity which is necessary to make the problem more tractable.
11.4 ROLL WAVES
|
|
Roll waves develop in open-channel flow when the Vedernikov number V > 1 (Craya, 1952; Chow, 1959). In natural channels, the condition V > 1 is seldom, if ever, met (Jarrett, 1982). Thus, roll waves are restricted to artificial channels lined with either concrete or masonry. Typically, roll waves appear as a train of waves that move downstream, as shown in Fig. 11-5 (Cornish, 1907).
|
The Vedernikov is defined as the ratio of relative kinematic wave celerity to relative dynamic wave celerity (Ponce, 1991):
|
(β - 1) u V = __________ (g h )1/2 | (11-2) |
in which β = exponent of the discharge-area rating (Eq. 10-52), u = mean velocity, h = flow depth, and g =
gravitational acceleration. Roll waves occur when the relative kinematic wave celerity exceeds the relative dynamic wave celerity.
Since kinematic waves transport mass, and (true) dynamic waves transport energy, roll waves occur at the threshold where mass and energy are being transported
at the same speed.
In practice, roll waves occur in steep artificial canals when the Vedernikov number
|
The condition
|
11.5 TIDAL WAVES
|
|
Tidal bores are rapidly varied unsteady free-surface flow features which take place in certain rivers in the proximity of their estuaries. A tidal waves occurs in an estuary for a large tidal range on or around either of the equinoxes (March 20 and September 22). Whether the tidal wave is able to move upstream into the river proper and develop into a recognizable bore of finite depth, depends largely on the cross-sectional geometry of the estuary. Tidal bores are more likely to form in smooth, hydraulically wide channels of relatively constant depth.
|
Large tidal bores have been observed on the Araguari river, in Brazil (Fig. 11-8), on the Chien Tang river, in China (Fig. 11-9), and in other selected estuaries around the world. Chow (1959) described the Hangchow bore at Haining on the Chien Tang river, China. The wavefront was about 16 ft high, traveling at high velocity. Seven miles after it could first be distinguished on the horizon, the wave had passed. The water reached a final height of about 28 ft within 30 minutes. The width of the river at the observation point was about 1 mile.
|
11.6 DEBRIS FLOWS
|
|
Debris flows are sudden accumulations of runoff containing great quantities of sediment particles, usually boulder size and above. Debris flows travel downstream at great speeds, destroying everything in their path and threatening life and property (Fig. 11-10).
|
Debris flows are induced by intense rains, but they can also be triggered by earthquakes. In Southern California, along the base of the San Gabriel Mountains, east of Los Angeles, rain-induced debris flows recur with predictable regularity. The factors leading to the formation of these debris flows are:
Tectonism
The San Gabriel Mountains are among the most tectonically active ranges in the United States
(Fig. 11-11). The uplift leads to slope steepening, which increases gravitational forces and maximizes erosion potential.
Wikimedia Commons Fig. 11-11 The San Gabriel Mountains, Southern California.
Chaparral ecosystem
The chaparral ecosystem is endemic to the region, surviving the long droughts by developing singular adaptations which rely on wax protective surface coating to suppress evapotranspiration (Fig. 11-12) (McPhee, 1989).

Fig. 11-12 Chaparral ecosystem, Tierra del Sol, San Diego County, California.
Wind
The region is home to the Santa Ana winds, which provide instant fire weather by featuring dry winds which can readily reach more than 40 miles per hour.
Fire
Fire follows wind after a long drought, with the chaparral not having burned for 30 years of more (Fig. 11-13).

Fig. 11-13 Aftermath of the Shockey fire, Tierra del Sol, California, on September 27, 2012.
Rain
Rain follows fire due to ash particles in the air promoting coalescence and raindrop formation.
The steep slopes covered with chaparral vegetation, followed by a sequence of wind, fire, and rain, is what triggers the debris flows in the Southern California region. During fire, the waxlike substances vaporize at the surface and recondense at a certain depth below the surface, producing the non-wettable layer, of 10 to 50 mm thickness. The accumulation of intense rainfall, exceeding 25 mm per hour, below the surface and above the non-wettable layer leads to the entrainment of large quantities of sediment which go on to constitute the debris flows. A typical rain-induced debris flow in Southern California may carry away 10-50 mm of soil in a few hours. By way of comparison, normal erosion rates are typically less than 1 mm per year.
Earthquake-triggered slides
Massive debris flows can also be triggered by earthquakes. Such was the case of the Huascaran slide on May 30, 1970, in Peru, which buried the town of Yungay, killing more than 20,000 people (Fig. 11-14). The town has since been rebuilt at a location just north of the ill-fated site.
|
11.7 LAHARS
|
|
Lahars are debris flows triggered by snowmelt, following a volcanic eruption and subsequent sudden melting of the snowcap. The word lahar originated in Indonesia, where the phenomenon is common. Lahars have the consistency, viscosity, and approximately the same density as concrete; fluid when moving, and solid when stopped (Fig. 11-15).
|
Lahars can be massive and deadly, as shown by the November 13, 1985 eruption of the Nevado del Ruiz volcano, in Colombia. Four lahars came down the river valleys on the volcano flanks. The largest of them virtually destroyed the town of Armero, burying it under 5 m of mud and debris, and killing more than 75% of its 28,700 inhabitants (Fig. 11-16).
|
QUESTIONS
|
|
What bedforms develop under upper regime in alluvial channel flow?
When do surges form in open-channel flow?
What is a kinematic shock?
What conditions are necessary for a kinematic wave to steepen into a kinematic shock?
When do roll waves develop?
Do roll waves develop always in steep channels?
Where are tidal bores are more likely to form?
What is a debris flow?
What conditions are conducive to the development of debris flows in the Southern California climate?
What is a lahar?
PROBLEMS
|
|
Calculate the time of opening of a canal gate under the following flow conditions: flow depth
do = 1.2 m, flow velocity uo = 1.5 m/s, and channel slope So = 0.001.A certain channel has a dimensionless Darcy-Weisbach friction factor f = 0.0035. The channel slope is So = 0.014. Determine if this flow condition is stable for Chezy friction in a hydraulically wide channel.
REFERENCES
|
|
Brock, R. R. 1967. Development of roll waves in open channels. Report No. KH-R-16, W. M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, California,
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York.
Cornish, V. 1907. Progressive waves in rivers. The Geographical Journal. Vol. 29, No.1, January, 23-31.
Craya, A. 1952. The criterion for the possibility of roll-wave formation. Gravity Waves, Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.
Hjalmarson, H. W. 1984. Flash flood in Tanque Verde Creek, Tucson, Arizona. Journal of Hydraulic Engineering, Vol. 110, No. 12, 1841-1852.
Jarrett, R. D. 1984. Hydraulics of high-gradient streams. Journal of Hydraulic Engineering, Vol. 110, No. 11, 1519-1539.
Kibler, D. F., and D. A. Woolhiser. 1970. The kinematic cascade as a hydrologic model. Hydrology Paper No. 39, Colorado State University, Ft. Collins, Colorado.
Lighthill, M. J., and G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
McPhee, J. 1989. The Control of Nature. Farrar Straus Giroux, New York.
Ponce, V, M., and D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 4, April, 600-611.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.
Ponce, V, M., and M. P. Maisner. 1993. Verification of theory of roll wave formation. Journal of Hydraulic Engineering, ASCE, Vol. 119, No. 6, June, 768-773.
Ponce, V, M., Y. R. S.Rao, and N. M. Mansury. 1999. Time of opening of irrigation canal gates. Journal of Hydraulic Engineering, ASCE, Vol. 125, No. 9, September, 979-980.
Phillips, J. V., and T. L. Ingersoll. 1998. Verification of roughness coefficients for selected natural and constructed stream channels in Arizona. U.S. Geological Survey Professional Paper 1584, Washington, D.C.
Simons, D. B., and E. V. Richardson. 1966. Resistance to flow in alluvial channels. U.S. Geological Survey Professional Paper 422-J, Washington, D.C.
| http://openchannelhydraulics.sdsu.edu |
|
140902 08:15 |