QUESTIONS
What conservation
laws are used in the description of steady gradually varied flow?
Steady mass and energy are used in the description of steady gradually varied flow.
What conservation
laws are used in the description of unsteady gradually varied flow?
Unsteady mass and momentum are used in the description of unsteady gradually varied flow.
What forces are acting in a control volume in unsteady
gradually varied flow?
Four forces: (1) gravitational force, (2) frictional force,
(3) the force due to the pressure gradient,
and (4) inertia force.
What waves types are common in unsteady open-channel flow?
Five wave types: (1) kinematic wave, (2) kinematic-with-diffusion wave,
(3) dynamic wave, (4) steady-dynamic wave, and (5) mixed kinematic-dynamic wave.
To what problems do kinematic waves apply?
Kinematic waves apply to overland flow and to steep channels, generally greater
than 1% slope.
To what problems do diffusion waves apply?
Diffusion waves
apply to flood routing in streams and rivers, with intermediate bottom slopes (0.01 > So > 0.0001).
How is Lo defined?
Lo is defined as ho/So,
i.e., it is the length of channel that it takes the uniform flow to drop a head equal to its depth.
What is the dimensionless wavenumber?
The dimensionless wavenumber is the wavenumber 2π/L made dimensionless
by multiplying it by Lo.
What is the dimensionless relative celerity of kinematic waves under
Chezy friction in hydraulically wide channels?
The dimensionless relative celerity of kinematic waves under
Chezy friction in hydraulically wide channels is 0.5.
What is the dimensionless relative celerity of dynamic waves under
Chezy friction in hydraulically wide channels?
The dimensionless relative celerity of dynamic waves under
Chezy friction in hydraulically wide channels is the reciprocal of the Froude number.
What are three ways of expressing the convective celerity of kinematic
waves?
There are three ways of expressing the convective celerity of kinematic waves:
(1) βV, (2) dQ/dA, and (3) (1/T ) dQ/dy.
What is the neutral-stability Froude number for triangular channels
with Chezy friction?
The neutral-stability Froude number for triangular channels
with Chezy friction is Fns = 4.
What is the neutral-stability Froude number for hydraulically wide channels
with Manning friction?
The neutral-stability Froude number for triangular channels
with Chezy friction is Fns = 1.5.
What is the basis of the Muskingum-Cunge method?
The matching of the physical diffusivity of the diffusion wave
with the numerical diffusivity of the Muskingum-type numerical analog of the kinematic wave equation.
What is Hayami's contribution to flood routing?
Hayami developed the diffusion analogy of flood waves,
by which flood waves are calculated using a convection-diffusion equation.
For what value of Vedernikov number are kinematic
and dynamic hydraulic diffusivities the same?
For V = 0, i.e., for very low Froude number flows.
For what value of Vedernikov number does the
dynamic hydraulic diffusivity vanish?
For V = 1.
What part of the flood routing does the Muskingum parameter X
account for?
The parameter X accounts for the storage portion of the routing.
For a given flood event, there is a value of X for which the storage in the calculated outflow hydrograph
matches that of the measured outflow hydrograph.
What is numerical diffusion?
Numerical diffusion is a diffusion in the results, which is
attributable
to the first-order error due to the discrete (finite) grid.
What is numerical dispersion?
Numerical dispersion is a dispersion in the results, which is
attributable
to the second-order error due to the discrete (finite) grid.
What is the advantage of the Muskingum-Cunge method?
A unique feature of the Muskingum-Cunge method, which sets
it apart from other numerical kinematic wave models, is the grid independence of the calculated outflow
hydrograph. If numerical dispersion is minimized, the calculated outflow at the downstream end of a channel
reach will be essentially the same, regardless of how many subreaches are used in the computation.
When will the Muskigum-Cunge method fail to give good results?
For the Muskingum-Cunge method to improve on the Muskingum method,
it is necessary that the routing parameters evaluated at channel cross sections be representative
of the channel reach under consideration. If this is not the case, the results may not be accurate.
How is the downstream boundary specified in a mixed
kinematic-dynamic model if increased accuracy is desired?
By artificially
extending the channel several subreaches downstream, and specifying a kinematic
rating at the newly defined downstream boundary, while giving the loop a chance to develop
at the upstream cross section of interest.
PROBLEMS
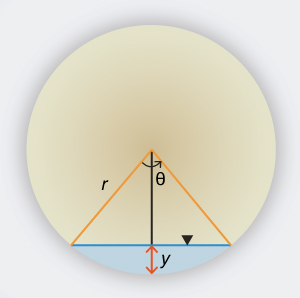
Derive the expression for the angle θ
in a circular channel (culvert) as a function of flow depth y and diameter
D, where D = 2r (Fig. 1-14).
Fig. 1-14 Definition sketch for a circular channel.
http://openchannelhydraulics.sdsu.edu
140815 14:45