|
|
|
CHAPTER 7: GRADUALLY VARIED FLOW |
7.1 EQUATION OF GRADUALLY VARIED FLOW
|
|
The flow is gradually varied when the discharge Q is constant but the other hydraulic variables (A, V, D, R, P, and so on) vary gradually in space. The basic assumptions of gradually varied flow are:
The flow is steady, i.e., none of the hydraulic variables vary in time.
The streamlines are essentially parallel; thus, the pressure distribution in the vertical direction is hydrostatic, i.e., proportional to the flow depth.
The head loss is the same as that corresponding to uniform flow; therefore, the uniform flow formula may be used to evaluate the energy slope.
The value of Manning's n is the same as that of uniform flow.
The slope of the channel is small.
The pressure correction factor cosθ ≅ 1.
There is negligible air entrainment.
The conveyance is an exponential function of the flow depth (except for the case of circular culverts).
The roughness (Manning's n) is independent of the flow depth (only an approximation) and is constant throughout the reach under consideration.
|
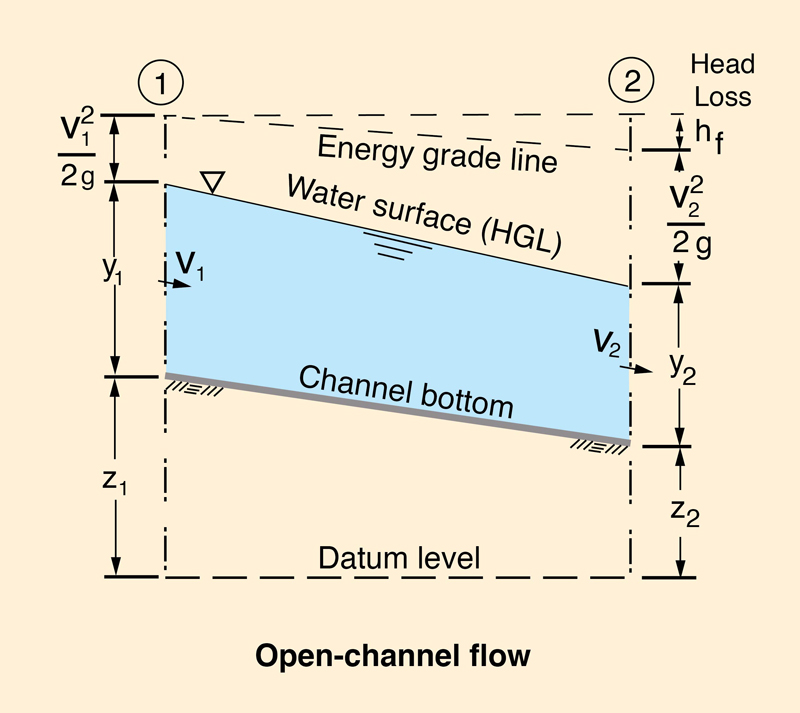
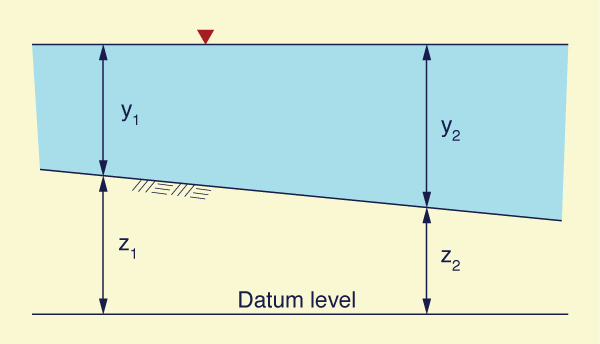
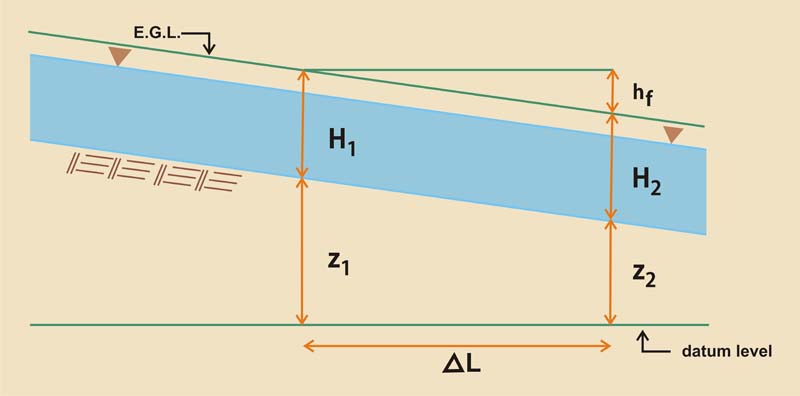
Under gradually varied flow, the gradient of hydraulic head is (Fig. 7-1):
|
dH d V 2 _____ = ___ ( z + y + _____ ) = - Sf dx dx 2g | (7-1) |
The negative sign in front of the friction slope Sf is required because the flow direction is from left to right, while the derivative is taken from right to left, by convention. By definition, the friction slope is:
|
hf Sf = _____ ΔL | (7-2) |
in which ΔL = length of the channel reach under consideration.
The gradient of specific energy is:
|
dE d V 2 dz _____ = ___ ( y + _____ ) = - ____ - Sf dx dx 2g dx | (7-3) |
The gradient of the channel bed, or channel slope (bottom slope), is:
|
dz z2 - z1
_____ = ________ dx ΔL | (7-4) |
|
dz z1 - z2
- _____ = ________ = So dx ΔL | (7-5) |
Therefore, the gradient of specific energy is:
|
dE d V 2 _____ = ___ ( y + _____ ) = So - Sf dx dx 2g | (7-6) |
Under steady flow: Q = V A = constant. Therefore:
|
d Q 2 ____ ( y + _______ ) = So - Sf dx 2g A2 | (7-7) |
|
dy d Q 2 _____ + _____ ( _______ ) = So - Sf dx dx 2g A2 | (7-8) |
|
dy Q 2 dA _____ - ( ______ ) _____ = So - Sf dx g A3 dx | (7-9) |
|
dy Q 2 dA dy _____ - ( ______ ) _____ _____ = So - Sf dx g A3 dy dx | (7-10) |
Using Eq. 3-11:
|
dy Q 2 T dy _____ - ( ________ ) _____ = So - Sf dx g A3 dx | (7-11) |
Therefore, the flow-depth gradient is:
|
dy So - Sf _____ = _______________________ dx 1 - [(Q 2 T ) / (g A3)] | (7-12) |
The friction slope based on the Chezy equation (Eqs. 5-10 and 2-4) is:
|
Q 2 Sf = ____________ C 2 A2 R | (7-13) |
Since R = A / P :
|
Q 2 P Sf = _________ C 2 A3 | (7-14) |
Substituting Eq. 7-14 into Eq. 7-12, the flow-depth gradient is:
|
dy So - [(Q 2 P ) / (C 2 A3)] _____ = ___________________________ dx 1 - [(Q 2 T ) / (g A3)] | (7-15) |
|
dy So - (g/C 2) (P / T ) [(Q 2 T ) / (g A3)] _____ = _______________________________________ dx 1 - [(Q 2 T ) / (g A3)] | (7-16) |
The square of the Froude number is (Eq. 3-12):
|
Q 2 T F 2 = _________ g A3 | (7-17) |
Substituting Eq. 7-17 into Eq. 7-16:
|
dy So - (g/C 2) (P / T ) F 2 _____ = _________________________ dx 1 - F 2 | (7-18) |
Substituting Eq. 5-12 into Eq. 7-18:
|
dy So - f (P / T ) F 2 _____ = _____________________ dx 1 - F 2 | (7-19) |
Therefore, the depth gradient (dy/dx) is a function of:
Channel slope So,
Friction coefficient f,
Ratio of wetted perimeter to top width P / T, and
Froude number.
For dy/dx = 0, Eq. 7-19 reduces to a statement of uniform flow:
|
So = f (P / T ) F 2 | (7-20) |
For F = 1, Eq. 7-20 reduces to a statement of critical uniform flow:
|
So = f (Pc / Tc ) = Sc | (7-21) |
in which Sc = critical slope, i.e., the channel slope for which the flow is critical.
In terms of critical slope (Eq. 7-21), the flow-depth gradient is:
|
dy So - (P / T ) (Tc / Pc )
Sc F 2 _____ = ________________________________ dx 1 - F 2 | (7-22) |
For (P / T ) ≅ (Pc / Tc ), i.e., for a constant ratio (P / T) with flow depth, Eq. 7-22 reduces to:
|
dy So -
Sc F 2 _____ = _______________ dx 1 - F 2 | (7-23) |
For conciseness, the flow-depth gradient can be written as:
|
dy Sy = _____ dx | (7-24) |
Substituting Eq. 7-24 into Eq. 7-23, the flow-depth gradient is:
|
Sy (So / Sc) - F 2 ____ = __________________ Sc 1 - F 2 | (7-25) |
Equation 7-25 (or 7-23) is the gradually varied flow equation. The depth gradient Sy is a function only of: (1) channel slope So, (2) critical slope Sc, and (3) Froude number F.
|
Note on the applicability of Eq. 7-25
Strictly speaking,
Eq. 7-25 applies only for
the case (P / T ) (Tc / Pc ) = 1, which is the same as
(P / T ) = (Pc / Tc ); that is,
for a constant ratio (P / T ), regardless
of flow depth. This condition is less restrictive that the (asymptotic) hydraulically wide
channel condition, for which (P / T ) = 1.
Therefore, for a hydraulically wide channel, for which P ≅ T,
it follows that: |
7.2 CHARACTERISTICS OF FLOW PROFILES
|
|
In Eq. 7-25, the sign of the left-hand side (LHS) is that of Sy (numerator), since Sc (denominator) is always positive (friction is always positive). The sign of Sy (i.e, the sign of the LHS) may be one of three possibilities:
- A positive value, leading to RETARDED FLOW (BACKWATER),
- A zero value, leading to UNIFORM FLOW (NORMAL), or
- A negative value, leading to ACCELERATED FLOW (DRAWDOWN).
In the right-hand side (RHS) of Eq. 7-25, there are three possibilities for the numerator (USDA Soil Conservation Service, 1971):
- So / Sc > F 2, leading to SUBNORMAL FLOW,
- So / Sc = F 2, leading to NORMAL FLOW, or
- So / Sc < F 2, leading to SUPERNORMAL FLOW.
There are three possibilities for the denominator:
- 1 > F 2, leading to SUBCRITICAL FLOW,
- 1 = F 2, leading to CRITICAL FLOW, or
- 1 < F 2, leading to SUPERCRITICAL FLOW.
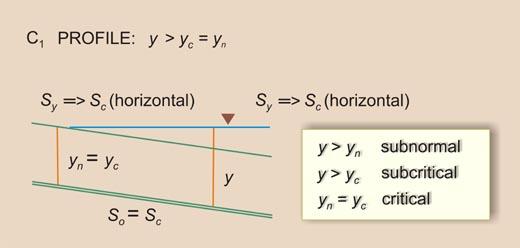
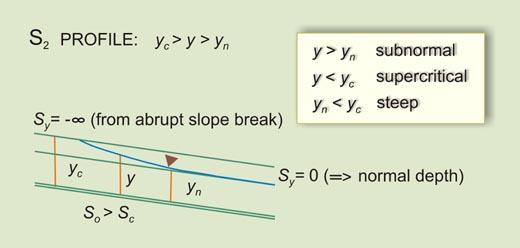
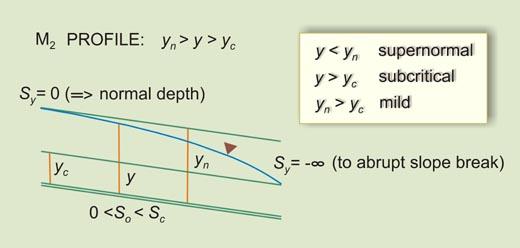
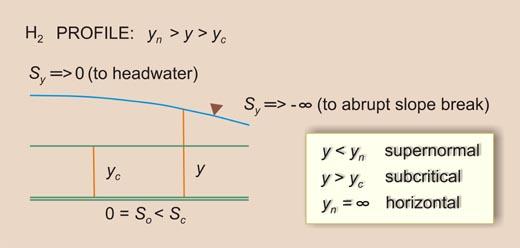
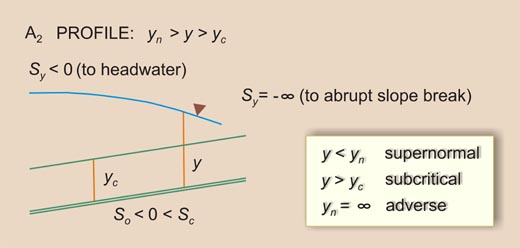
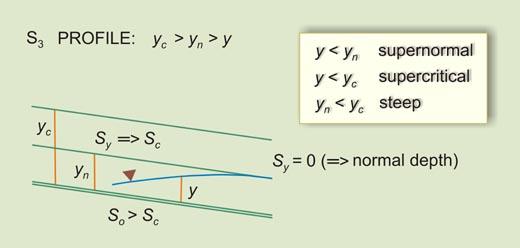
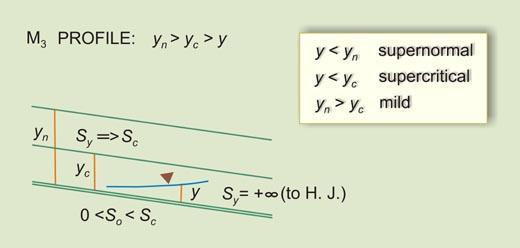
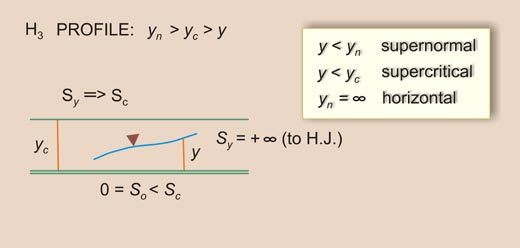
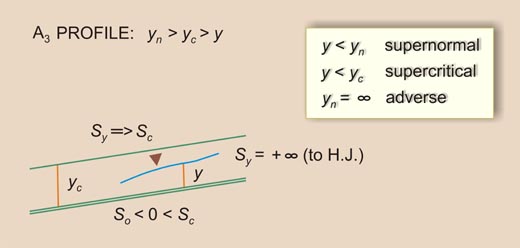
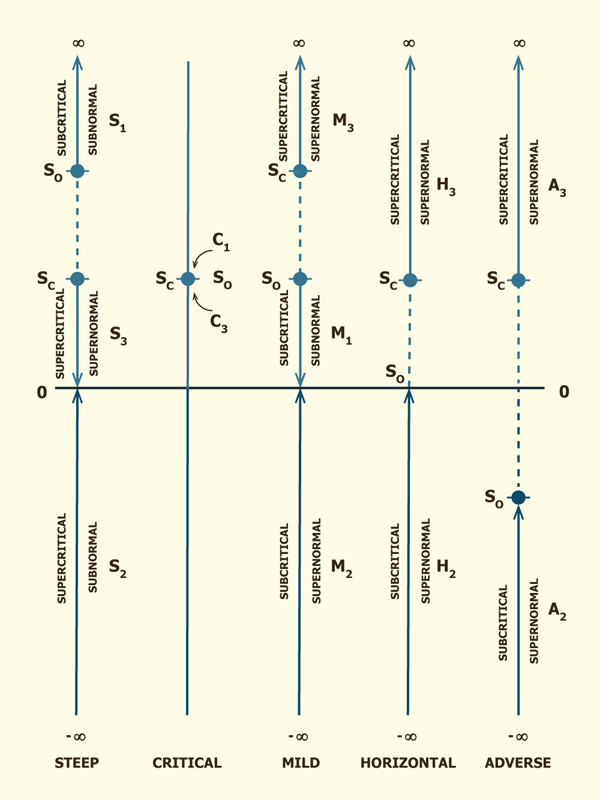
Given the above inequalities, there arise three types (or families) of water-surface profiles, shown in Table 7-1. The total number of profiles is 12. A summary is shown in Table 7-2.
Table 7-1 Types of water-surface profiles.
| Type | Description
| Numerator and denominator of RHS | of Eq. 7-25
Sign | of LHS Flow | profile
I
| Subnormal/subcritical flow |
Both numerator and denominator are positive
|
+ |
Retarded |
II | A
| Subnormal/supercritical flow | Numerator is positive and denominator is negative |
- |
Accelerated | B | Supernormal/subcritical flow | Numerator is negative and denominator is positive |
- |
Accelerated |
III | Supernormal/supercritical flow
| Both numerator and denominator are negative |
+ |
Retarded |
Figure 7-14 shows a graphical representation of flow-depth gradients in water-surface profile computations. The arrows indicate the direction of computation.
7.3 LIMITS TO WATER SURFACE PROFILES
The flow-depth gradients vary between five (5) limits (Fig. 7-14):
The theoretical limits to the water-surface profiles may be analyzed using Eq. 7-25, repeated here in a slightly different form:
Operating in Eq. 7-46:
For uniform (normal) flow: Sy = 0, and Eq. 7-48 reduces to:
For gradually varied flow: Sy ≠ 0, and Eq. 7-48 is subject to three (3) cases:
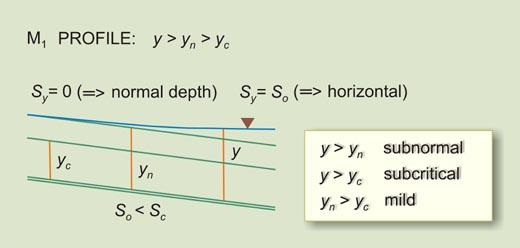
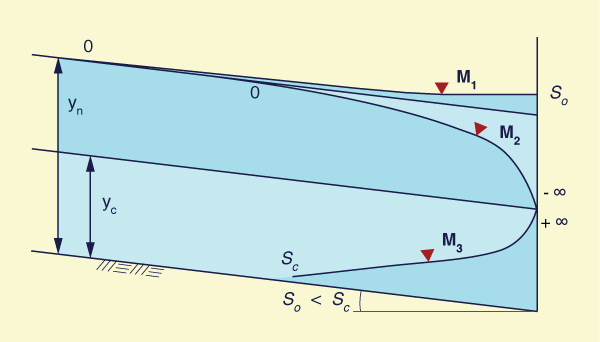
Table 7-3 and Fig. 7-16 show the typical occurrence of mild water-surface profiles.
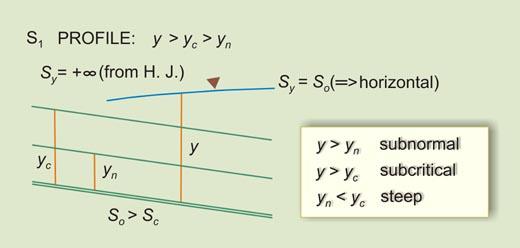
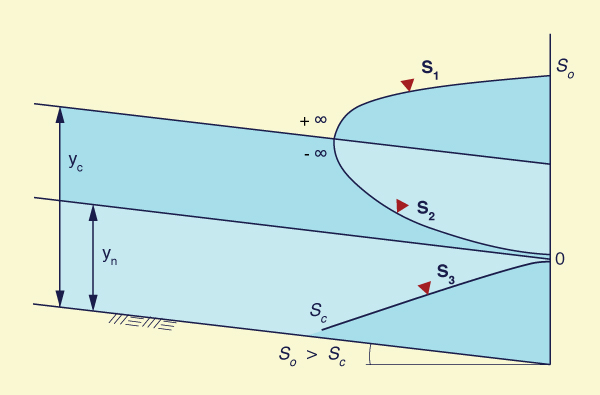
Table 7-4 and Fig. 7-17 show the typical occurrence of steep water-surface profiles.
7.4 METHODOLOGIES
There are two ways to calculate water-surface profiles:
The direct step method is applicable to prismatic channels, while the standard step method is applicable to any channel, prismatic and nonprismatic (Table 7-5). The direct step method is direct, readily amenable to use with a spreadsheet, and relatively straight forward in its solution. The standard step method is iterative and complex in its solution. In practice, the standard step method is represented by the Hydrologic Engineering Center's River Analysis System, referred to as HEC-RAS (U.S. Army Corps of Engineers, 2014). The direct step method applies particularly where data is scarce and resources are limited. The standard step method applies for comprehensive projects. The use of a widely accepted government program such as HEC-RAS enhances credibility. The required number of cross sections in the standard step method increases with the channel slope. Steeper channels may require more cross sections. Lesser cross sectional variability results in more reliable and accurate results. Note that extensive two- and three-dimensional flow features may not be accurately represented in the one-dimensional water-surface profile model.
7.5 DIRECT STEP METHOD EXAMPLE
Calculation of M2 and S2 profiles, upstream and downstream of a change in grade, from mild to steep
Input data:
Solution Calculate the normal depth and velocity, and critical depth and velocity, in the upstream and downstream channels. Use ONLINE CHANNEL 05. For the upstream channel: For the downstream channel: Calculation of critical slope for the upstream channel: Calculation of critical slope for the downstream channel: The calculation of the M2 water-surface profile is shown in Table 7-6. The following instructions are indicated:
In the direct step method, the accuracy of the computation depends on the size of depth interval The calculation of the S2 water-surface profile is shown in Table 7-7.
Online calculations The M2 water-surface profiles may be calculated online using ONLINE_WSPROFILES_22. Using the number of computational intervals n = 100, and number of tabular output intervals m = 100, the length of the M2 water-surface profile is calculated to be: ∑ ΔL = 147,691.5 m.
The S2 water-surface profiles may be calculated online using ONLINE_WSPROFILES_25. Using the number of computational intervals n = 100, and number of tabular output intervals m = 100, the length of the S2 water-surface profile is calculated to be: ∑ ΔL = 152.02 m.
QUESTIONS
PROBLEMS
REFERENCES
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York. U.S. Army Corps of Engineers. (2014). HEC-RAS: Hydrologic Engineering Center River Analysis System. USDA Soil Conservation Service. (1971). Classification system for varied flow in prismatic channels. Technical Release No. 47 (TR-47), Washington, D.C.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |