QUESTIONS

  1. When does uniform flow become unstable?

    Under a Vedernikov number V = 1, uniform flow becomes neutrally stable and this is conducive to the development of roll waves.

  2. What is the Chezy formula based on?

    The Chezy formua is based on a balance of frictional and gravitational forces.

  3. What is the difference between the Manning and Chezy formulas?

    In the Manning formula, the Chezy coefficient is not constant, but varies with the hydraulic radius to the 1/6 power.

  4. What is the minimum value of Manning's n that can be achieved in practice?

    n = 0.008, applicable to acrylic plastic (lucite).

  5. What is the range of values of Manning's n measured by Barnes?

    0.024 ≤ n ≤ 0.075.

  6. What is the range of values of Manning's n measured by Arcement and Schneider for flood plains?

    0.1 ≤ n ≤ 0.2.

  7. Why is the calculation of composite roughness using Eq. 5-43 only an approximation?

    The derivation of composite roughness, Eq. 5-43, assumes that the velocities are equal across the cross section of interest. However, there is a high probability that the velocities in inbank and overbank sections are not equal.

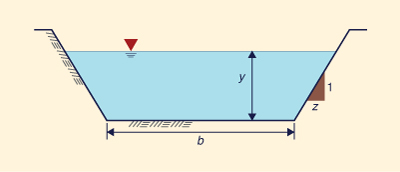
  8. What five input variables are used in the computation of uniform flow in a trapezoidal channel?

    (1) Discharge Q, (2) bottom width b, (3) side slope z, (4) bottom slope S, and (5) Mannings's n.

  9. Why is it better to use Newton's approximation to the root rather than relying solely on the function approximation to solve the normal depth problem?

    Because the Newton approximation, being based on the tangent, results in a lesser number of iterations to obtain the answer.

  10. What is the minimum ratio of reach length to hydraulic depth in the slope-area method?

    75.

  11. What is the exponent of the discharge-depth rating under laminar flow conditions?

    3.

  12. What is the exponent of the discharge-depth rating under turbulent Chezy friction in hydraulically wide channels?

    1.5

  13. What is the exponent of the discharge-depth rating under turbulent Manning friction in hydraulically wide channels?

    5/3 ≅ 1.667.

  14. Under what value of Froude number is the flow likely to become unstable under laminar flow conditions?

    For F = 0.5.

PROBLEMS

  1. Prove that the Darcy-Weisbach friction factor is related to Manning's n by the following relation:

    fD = 8 g n 2 / (k 2 R 1/3)

    in which fD = Darcy-Weisbach friction factor, g = gravitational acceleration, R = hydraulic radius, and k = constant specific for the system of units, equal to 1 in SI units and 1.486 in U.S. Customary Units. Express the relation in SI and U.S. Customary units.

    Chezy equation:

    V = C (RS)1/2

    V 2 = C 2 RS = ( C 2 /g ) gRS = ( 8 / fD ) gRS             [1]

    Manning equation:

    V = (k/n) R 2/3 S 1/2

    V 2 = (k 2/n 2) R 4/3 S             [2]

    Equating [1] and [2]:   (8 / fD ) g = (k 2/n 2) R 1/3

    fD = 8 g n 2 / (k 2 R 1/3)  ANSWER.

    In SI Units:   fD = 8 (9.806) n 2 / (12 R 1/3) = 78.45 n 2 / R 1/3  ANSWER.

    In U.S. Customary Units:   fD = 8 (32.17) n 2 / (1.486 2 R 1/3) = 116.55 n 2 / R 1/3  ANSWER.

  2. Calculate the discharge Q using the Manning equation, given: flow area A = 23.5 ft2; hydraulic radius R = 5.6 ft; channel slope S = 0.0025; Manning's n = 0.035.

    Q = 157.29 ft3/s  ANSWER.

  3. Calculate the discharge Q using the Manning equation, given: flow area A = 45 m2; hydraulic radius R = 6 m; channel slope S = 0.003; Manning's n = 0.04.

    Q = 203.46 m3/s  ANSWER.

  4. Given f = 0.0025, calculate the discharge Q for a flow area A = 12.4 m2, hydraulic radius R = 2.1 m; and channel slope S = 0.0015.

    Q = V A

    V = C R1/2 S1/2 = (C/g1/2) g1/2R1/2 S1/2

    f = g / C 2

    C/g1/2 = (1/f )1/2 = (1/0.0025)1/2 = 20

    Q = V A = 20 [ (9.806) (2.1) (0.0015) ]1/2 (12.4)

    Q = 43.586 m3/s  ANSWER.

  5. Given f = 0.0035, calculate the discharge Q for a flow area A = 18 ft2, hydraulic radius R = 4.5 ft; and channel slope S = 0.0018.

    Q = V A

    V = C R1/2 S1/2 = (C/g1/2) g1/2R1/2 S1/2

    f = g / C 2

    C/g1/2 = (1/f )1/2 = (1/0.0035)1/2 = 16.9

    Q = V A = 16.9 [ (32.17) (4.5) (0.0018) ]1/2 (18)

    Q = 155.28 ft3/s  ANSWER.

  6. Use ONLINE CHANNEL 01 to calculate normal depth, velocity, and Froude number for the following case: Q = 150 m3/s, b = 10 m, z = 2, So = 0.0005, n = 0.025.

    Normal depth yn = 4.452 m, normal velocity vn = 1.783 m, normal Froude number Fn = 0.327  ANSWER.

  7. Use ONLINE CHANNEL 01 to calculate normal depth, velocity, and Froude number for the following case: Q = 250 cfs, b = 20 ft, z = 1, So = 0.001, n = 0.030.

    Normal depth yn = 3.476 ft, normal velocity vn = 3.064 ft/s, normal Froude number Fn = 0.31  ANSWER.

  8. Using ONLINE CHANNEL 15, calculate the discharge for a prismatic channel with b = 20 ft, y = 3 ft, z = 2, n = 0.025, S = 0.0016.

    Definition sketch for a trapezoidal channel

    Fig. 5-18  Definition sketch for a trapezoidal channel.

    Q = 326.3 ft3/s  ANSWER.

  9. Using ONLINE CHANNEL 15, calculate the discharge for a prismatic channel with b = 6 m, y = 1 m, z = 1.5, n = 0.015, S = 0.0002.

    Q = 5.995 m3/s  ANSWER.

  10. A recent flood on Clearwater Creek has left observable water marks on a certain river reach. To estimate the flood magnitude, hydraulic data has been measured at two cross sections A and B, a distance of 1,850 ft apart. The reach fall between the cross sections is 9.1 ft and the average Manning's n is 0.035. The upstream flow area, wetted perimeter, and Coriolis α coefficient are 550 ft2, 55 ft, and 1.17; the downstream flow area, wetted perimeter, and α coefficient are 620 ft2, 52 ft, and 1.10. Use SLOPE AREA to calculate the flood discharge.

    Run SLOPE AREA with the given data to calculate the flood discharge Q = 8,841 cfs.  ANSWER.

  11. Calculate the unit-width discharge in an overland flow plane, under laminar flow, with mean depth of 1.5 cm and slope of 0.001. Assume water temperature T = 20oC. Report discharge in L/s/m.

    q = [ g S / (3 ν) ] ym3

    For T = 20oC:   ν = 1. × 10-6 m2/s

    q = [ ( 9.81 × 0.001 ) / (3 × 1. × 10 -6) ] (0.015)3

    q = 0.01103 m2/s

    q = 0.01103 m3/s/m

    q = 11.03 L/s/m  ANSWER.

http://openchannelhydraulics.sdsu.edu
140821 06:45

Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader.