QUESTIONS

  1. Why is β, the exponent of the rating, important in open-channel flow?

    The exponent of the rating, β, is important in open-channel flow because it embodies both the Froude and Vedernikov numbers.

  2. For a given discharge Q, what is the value of specific energy at critical flow?

    The specific energy is a minimum at critical flow.

  3. What is the relation between velocity head and hydraulic depth under critical flow?

    Under critical flow, the velocity head hv is equal to one-half of the hydraulic depth D.

  4. What is the difference bewteen primary and secondary waves in unsteady open-channel flow?

    While primary waves always travel downstream, secondary waves may travel upstream or downstream, depending on the flow conditions. In subcritical flow, w > u, and secondary waves are able to travel upstream. In supercritical flow, w < u, and secondary waves cannot travel upstream, instead traveling downstream.

  5. How are bottom slope, critical slope, and Froude number related in uniform flow?

    The bottom slope is directly proportional to the Froude number, when the constant of proportionality is the critical slope. Or, the bottom slope is directly proportional to the critical slope, when the constant of proportionality is the Froude number.

  6. Why is it extremely rare to have critical or supercritical flow in a natural channel?

    In a natural channel, the flow is able to freely interact with the boundary, increasing the "actual" or effective friction slope. In practice, the friction slope is not able to decrease to match the bottom slope, with the actual flow remaining subcritical, at least through most of its domain. Thus, it is extremely rare to have critical or supercritical flow in a natural channel.

  7. In a hydraulically wide channel, critical depth is only a function of what hydraulic variable?

    Unit-width discharge.

  8. How many types of control are there in open-channel flow?

    Two types: (1) section control, and (2) channel control. Section control acts at a cross section; channel control acts longitudinally along the channel.

  9. Under free-flowing conditions (low tailwater depth), only one gage measurement is required to determine the discharge in a Parshall flume. However, under submerged conditions (with high tailwater depth), two gage measurements are required.

  10. Why is full contraction necessary in flow measurement using a sharp-crested weir?

    Full contraction increases the measurement accuracy by providing a more precise channel control (a unique discharge-stage relation) in the immediate vinicity of the weir.

  11. Is the Cipolletti weir fully or partially contracted?

    Fully contracted.

  12. How is full contraction implemented in a standard suppressed rectangular weir?

    The elevation of the crest should be high enough, relative to the operating head, to assure full bottom crest contraction of the nappe. Therefore, the crest height P should be at least three times the operating hydraulic head H.

PROBLEMS

  1. Using the Chezy equation (Eq. 5-10), derive the formula for the critical slope Sc in a prismatic channel.

    Q = C A R 1/2 S 1/2

    Q2 = C 2 A 2 R S

    Sc = Q 2 / (C 2 Ac 2 Rc )

    Sc = Q 2 Pc / (C 2 Ac 3 )

    Sc = g Q 2 Tc Pc / (C 2 g Ac 3 Tc )

    (Q 2 Tc) / (g Ac3) = Fc 2 = 1

    Sc = (g/C 2) (Pc / Tc)

    Sc = f (Pc / Tc)  ANSWER.

  2. Using the Manning equation (Eq. 5-17 or Eq. 5-18), derive the formula for the critical slope Sc in a prismatic channel.

    Q = (k / n) A R 2/3 S1/2

    Q 2 = (k 2/n 2) A 2 R 4/3 S

    Sc = Q 2 / [(k 2/n 2) Ac 2 Rc 4/3 ]

    Sc = Q 2 / [(k 2/n 2) Ac 2 Rc Rc 1/3 ]

    Sc = Q 2 Pc / [(k 2/n 2) Ac 3 Rc 1/3 ]

    Sc = g Q 2 Tc Pc / [(k 2/n2) g Ac 3 Tc Rc 1/3 ]

    (Q 2 Tc) / (g Ac 3) = Fc 2 = 1

    Sc = g (Pc / Tc) / [(k/n) Rc1/6] 2

    Sc = g n 2 (Pc / Tc) / (k 2 Rc1/3)  ANSWER.

  3. Calculate the theoretical discharge over a broad-crested weir of length L = 22 ft, when the total head above the weir is H = 1.2 ft. Verify with ONLINE CHANNEL 14.

    Using ONLINE CHANNEL 14:  Q = 89.28 ft3/s.  ANSWER.

  4. Calculate the theoretical discharge over a broad-crested weir of length L = 8 m, when the total head above the weir is H = 0.5 m. Verify with ONLINE CHANNEL 14.

    Using ONLINE CHANNEL 14:  Q = 4.821 m3/s.  ANSWER.

  5. Calculate the critical depth corresponding to a unit-width discharge q = 1.36 m2/s.

    Using Eq. 4.25:  q = 0.573 m2/s.  ANSWER.

  6. Given a modified Darcy-Weisbach friction factor f = 0.003 and bottom slope S = 0.002. Calculate the Froude number.

    Using Eq. 4-8:   F = (S / f)1/2 = (0.002 / 0.003) 1/2 = 0.816  ANSWER.

  7. Use ONLINE CHANNEL 04 to calculate the critical slope for the following canal data: Q = 11 m3/s, b = 1.5 m, z = 1, S = 0.0006, n = 0.013.

    Sc = 0.002348  ANSWER.

  8. Use ONLINE CHANNEL 04 to calculate the critical slope for the following canal data: Q = 35 ft3/s, b = 3 ft, z = 1, S = 0.001, n = 0.015.

    Sc = 0.004108  ANSWER.

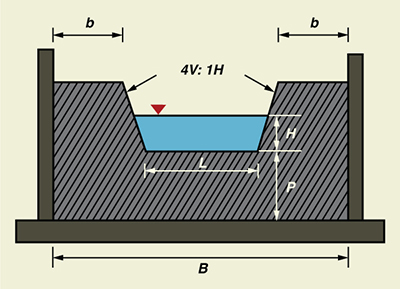
  9. Use ONLINE CIPOLLETTI to calculate the weir discharge, given head H = 1 ft, length L = 3.2 ft, height P = 4 ft, and width B = 6 ft.

    Definition sketch for Cipolletti weir

    Fig. 1-18  Definition sketch for a Cipolletti weir.

    Discharge Q = 10.774 ft3/s  ANSWER.

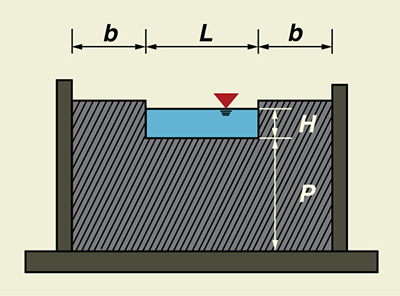
  10. Use ONLINE STANDARD CONTRACTED RECTANGULAR to calculate the weir discharge, given head H = 0.5 m, length L = 3 m, height P = 3 m, and width b = 1.5 m.

    Definition sketch for a standard contracted rectangvular weir.

    Fig. 1-19  Definition sketch for a standard contracted rectangular weir.

    Discharge Q = 1884.97 L/s  ANSWER.

http://openchannelhydraulics.sdsu.edu
140820 14:15

Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader.