QUESTIONS
What is the difference between total energy and specific energy?
Total energy considers the bed elevation;
specific energy does not. Therefore, specific energy is applicable to channels of very mild slope, where the
difference in bed elevation can be neglected.
What is critical flow in terms of specific energy?
Critical flow corresponds to minimum specific energy.
What causes a hydraulic drop?
The hydraulic drop is triggered by a
sharp depression in the water surface, usually caused by an abrupt change in bottom elevation.
Why is the flow depth at a free overfall less than critical?
Flow in the proximity of a free overfall is usually rapidly
varied; therefore, the brink depth is somewhat smaller than the critical depth computed by the theory of parallel flow.
What causes a hydraulic jump?
The hydraulic jump is triggered by an abrupt rise in the water surface as the flow progresses downstream.
Why is momentum unsteady?
Momentum is equal to a force integrated over a
period of time; therefore, it is essentially unsteady.
What is the body force considered in open-channel flow?
The gravitational force.
What is the magnitude of the body force in a horizontal channel?
Zero; the gravitational force does not exist in a horizontal channel.
What is the difference between alternate depths and sequent
depths?
Alternate depths have the same specific energy; sequent depths
do not.
Where does specific force apply?
In a horizontal channel of short length, where the gravitational
force is zero and the frictional force can be neglected, compared to the remaining forces
(pressure-gradient force and inertia force).
For what type of problems is specific force used?
For those problems where forces can be shown to play a
significant role in the solution.
PROBLEMS
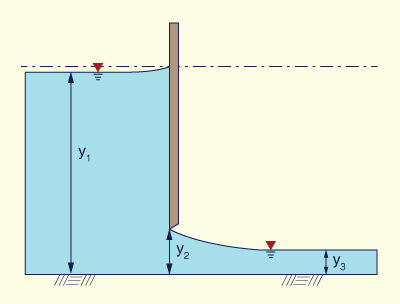
Derive the relation for the discharge
per unit of width q under a sluice gate, as a function of upstream depth y1
and downstream depth y3.
Fig. 3-12 Discharge under a sluice gate.
The conservation of specific energy between the u/s flow and the d/s flow is:
y1 + v12/(2g) = y3 + v32/(2g)
y1 + q2/(2gy12) = y3 + q2/(2gy32)
[q2/(2g)] [ (1/y12) - (1/y32) ] = y3 - y1
q2/(2g) = (y12 y32) / (y1 + y3)
q = y1 y3 [ 2 g / (y1 + y3) ] 1/2 ANSWER.
Prove that the equation derived in the previous problem (Problem 1) is mathematically equivalent
to the equation based on y1
and y2 on used in ONLINE CHANNEL 13.
The two equations are mathematically the same.
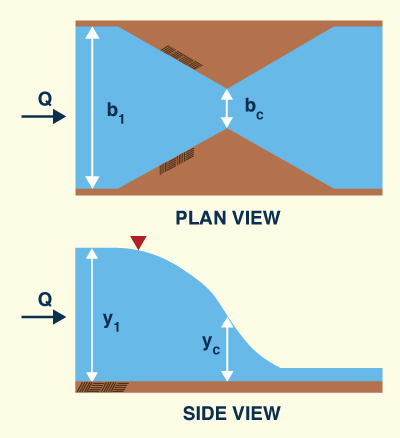
Using the specific energy principle, derive the formula for the
dimensionless throat width of a channel constriction that forces critical flow through it [Henderson (1966), p. 267].
σ = bc / b1 = (27)1/2 F1 / (2 + F12) 3/2
Fig. 3-13 Critical width constriction using specific energy. The specific energy for the u/s flow is:
E1 = y1 + v12/(2g) = y1 [ 1 + (F12/2) ]
yc = (2/3) E1 = (2/3) y1 [ 1 + (F12/2) ]
yc / y1 = (2/3) [ 1 + (F12/2) ] = (1/3) (2 + F12)
From water continuity:
Q = v1 y1 b1 = vc yc bc
σ = bc / b1 = (v1 y1) / (vc yc)
σ = v1 / [ vc (yc / y1) ]
σ = v1 / [ ( g yc ) 1/2 (yc / y1) ]
σ = v1 / [ ( g y1 ) 1/2 (yc / y1) 3/2 ]
σ = F1 / (yc / y1) 3/2
σ = F1 / [ (1/3) (2 + F12) ] 3/2
σ = (27)1/2 F1 / (2 + F12) 3/2 ANSWER.
Use ONLINE CHANNEL 17 to calculate the required
throat width bc for the following upstream conditions: y1 = 2.2 m, v1 = 1.2 m/s,
and b1 = 3.2 m. What would be the required throat width if the upstream channel width is b1 = 2.2 m?
Q = v1 y1 b1 = 1.2 × 2.2 × 3.2 = 8.448 m3/s
Run ONLINE CHANNEL 17 to calculate bc = 1.445 m. ANSWER.
Q = v1 y1 b1 = 1.2 × 2.2 × 2.2 = 5.808 m3/s
Run ONLINE CHANNEL 17 to calculate bc = 0.994 m. ANSWER.
Using the specific force principle, show that the force fo (in kN/m) exerted by a blunt obstruction at the bottom of a wide rectangular channel is:
where γ = unit weight of water, F1 = upstream Froude number, y1 = upstream flow
depth, and α = y2/y1, where y2 = downstream flow depth (after the obstruction).
Given q = 1.5 m2/s, v1 = 1.0 m/s, and α = 0.91, calculate the force fo.
Assuming the flow is from left to right, in what direction is the force fo acting?
The conservation of specific force leads to the force ON the obstruction:
fo, ON = f1 - f2
fo, ON = γ [ q2/(gy1) + (y12/2) ] - γ [ q2/(gy2) +
(y22/2) ]
fo, ON = γ [ q2/(gy1) + (y12/2) - q2/(gy2) -
(y22/2) ]
fo, ON = γ y12 [ q2/(gy13) + 1/2
- q2/(gy2y12) - y22/(2y12) ]
fo, ON = γ y12 [ q2/(gy13) + 1/2
- q2/(g y13α) - (α2/2) ]
fo, ON = γ y12 [ F12 + 1/2 - (F12 / α) - (α2/2) ]
fo, ON = γ y12 { [ (1 - α 2) / 2 ] + [ 1 - (1/α ) ]
F12 }
The force exerted by the obstruction is: fo = - fo, ON
fo = - γ y12 { [ (1 - α 2) / 2 ] + [ 1 - (1/α ) ]
F12 }
y1 = q/v1 = 1.5 / 1.0 = 1.5 m.
y12 = (1.5)2 = 2.25 m2
y13 = (1.5)3 = 3.375 m3
γ = 9.806 kN/m3
α = 0.91
F12 = q2/(g y13) = (1.5)2 / (9.806 × 3.375 ) = 0.068
fo = - 9.806 (2.25) [ (1 - 0.8281)/2 + 0.068 (1 - (1/0.91) ) ] = - 1.748 kN/m ANSWER.
Because fo is negative, it acts in a direction opposite to the flow, i.e., from right to left. ANSWER.
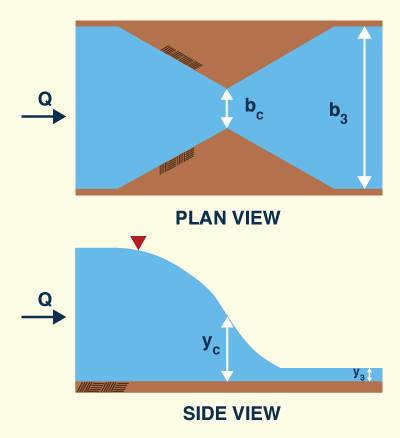
Using the specific force principle, derive the formula for the
dimensionless throat width of a channel constriction that forces critical flow through it [modified from Henderson (1966), p. 267].
σ = bc / b3 = (3)3/4 F3 / (1 + 2 F32) 3/4
Fig. 3-14 Critical width constriction using specific force.
The momentum-based equation is derived by equating the specific force at critical flow at the
contraction (Section 2, or Section c) with the specific force at the downstream flow section (Section 3).
The specific force at the downstream flow section is:
Replacing the discharge Q:
From continuity:
Thus:
The Froude number at the downstream section is defined as follows:
Thus, Eq. 5 reduces to:
The specific force at the contraction is:
Replacing the discharge Q:
From continuity:
Or:
Replacing Eq. 6 in Eq. 11:
By definition, the critical depth is:
Or:
From continuity:
Or:
Replacing Eq. 6 in Eq. 16:
Replacing Eq. 17 in Eq. 12:
Reducing terms:
Equating Eqs. 7 and 19:
Reducing:
ANSWER.
Using ONLINE LIMITING CONTRACTION,
calculate the limiting contraction ratios using both energy and momentum principles, for a Froude number F = 0.3.
Using the specific energy principle, for F = 0.3: σ = 0.516 ANSWER.
Using the specific force principle, for F = 0.3: σ = 0.604 ANSWER.
Using ONLINE LIMITING CONTRACTION SET,
calculate the limiting contraction ratios using both energy and momentum principles, for Froude numbers is the range 0.1 ≤ F ≤ 2.0, at intervals of 0.1.
Discuss the results.
Using the specific energy principle, σ varies between 0.182 and 1.0, for F = 0.1 to F = 1.0; then, it reduces to σ = 0.707 at F = 2. ANSWER.
Using the specific force principle, σ varies between 0.225 and 1.0, for F = 0.1 to F = 1.0; then, it reduces to σ = 0.877 at F = 2. ANSWER.
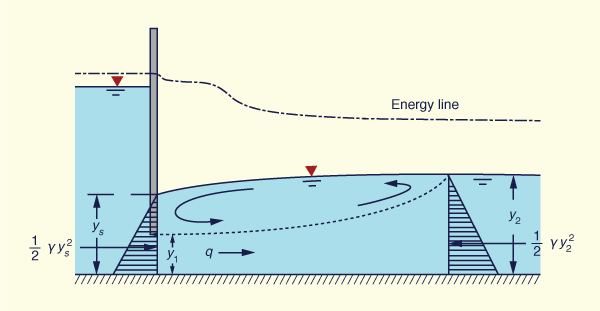
A submerged hydraulic jump
occurs immediately downstream of a sluice outlet in a rectangular channel.
Using the momentum principle, prove that the ratio of submerged depth ys
to tailwater depth y2 is:
Fig. 3-15 A submerged hydraulic jump at a sluice outlet. The specific force principle applied between the upstream and downstream sections is:
ANSWER.
M3 = M2 = Mc
(1)
q32 y32
M3 = _______ + _______
g y3 2(2)
Q2 y32
M3 = ___________ + ______
g y3 b32 2(3)
Q = v3 y3 b3 = vc yc bc
(4)
v32 y32 y32
M3 = __________ + ______
g y3 2(5)
v32
F32 = _______
g y3
(6)
1
M3 = y32 ( ____ + F32 )
2 (7)
qc2 yc2
Mc = _______ + _______
g yc 2(8)
Q2 yc2
Mc = ___________ + ______
g yc bc2 2(9)
v32 y32 b32 yc2
Mc = _______________ + ______
g yc bc2 2(10)
v32 y33 b32 yc2
Mc = _______________ + ______
g yc bc2 y3 2(11)
F32 y33 yc2
Mc = ___________ + ______
σ2 yc 2(12)
q2
yc = ( ____ ) 1/3
g (13)
Q2
yc = ( ________ ) 1/3
bc2g (14)
v32 y32 b32
yc = ( _____________ ) 1/3
bc2g (15)
v32 y33 b32
yc = ( _____________ ) 1/3
bc2g y3 (16)
F32 y33
yc = ( _________ ) 1/3
σ2 (17)
F32 y32 σ2/3 F32 y33
Mc = ______________ + (1/2) ( _________ )2/3
σ2 F32/3 σ2(18)
F34/3
Mc = (3/2) ( ________ ) y32
σ4/3 (19)
1 F34/3
( ___ + F32 ) = (3/2) ( ________ )
2 σ4/3 (20)
33/4 F3
σ = _____________________
( 1 + 2 F32 ) 3/4 (21)
ys y2
_____ = [ 1 + 2 F22 ( 1 - _____ ) ] 1/2
y2 y1 (22)
V1 2y1 ys 2
V2 2y2 y2 2
_________ + ______ = ________ + ______
g 2 g 2
(23)
ys 2
V2 2y2 y2 2 V1 2y1
______ = ________ + ______ - ________
2 g
2 g
(24)
ys 2
2 V2 2 2 2 V1 2y1
______ = _______ + _____ - __________
y2 2 gy2
2 g y2 2
(25)
ys 2
2 V2 2 2
2 V1 2y1 V2 2
______ = _______ + _____ - _______________
y2 2 gy2
2 g y2 2 V2 2
(26)
From continuity:
V1 y1 = V2 y2
(27)
ys 2
y2
______ = 2 F22 + 1 - 2 F22 _____
y2 2
y1
(28)
ys y2
_____ = [ 1 + 2 F22 ( 1 - _____ ) ] 1/2
y2 y1 (29)
http://openchannelhydraulics.sdsu.edu
141110 13:30