QUESTIONS
What is the difference between flow depth d
and hydraulic depth D?
The flow depth d
is the distance from the water surface
to the channel bottom. It has particular application to trapezoidal or rectangular channels,
where it is a constant. The hydraulic depth D is the ratio of flow area A
to top width T. In a rectangular hydraulically wide channel, d and D
are approximately the same.
Is unsteady uniform flow possible? Why not?
Unsteady uniform flow does not exist in nature, because the flow cannot be uniform and unsteady at the same time. The word "unsteady" implies nonequilibrium; thus, unsteady equilibrium flow does not exist.
What four forces are acting in the momentum balance
in open-channel flow?
In general, four forces are active in a control volume in open-channel flow. These forces are due to friction, gravity, the pressure (flow depth) gradient, and inertia.
What is a kinematic wave?
Kinematic waves are those where the momentum balance is expressed in terms of the frictional and gravitational forces only.
What is a dynamic wave according to Lagrange?
According to Lagrange, dynamic waves are those where the momentum balance is expressed in terms of the pressure-gradient and inertial forces only.
What is the Froude number?
The Froude number is the ratio of
mean velocity u to the relative celerity of dynamic waves
What is the Vedernikov number?
The Vedernikov number is the ratio of
the relative celerity of kinematic waves v = (β - 1)u to the
relative celerity of dynamic waves
What is neutrally stable flow?
Under neutrally stable flow, the
relative kinematic wave celerity v is equal to the relative dynamic
wave celerity w and, therefore, surface waves (perturbations) neither attenuate nor amplify.
What is the normal range in the exponent β
of the
discharge-flow area rating in open-channel and free-surface flow?
The value of β
varies with the type of friction regime (laminar, transitional, or turbulent;
and turbulent Manning or Chezy) and cross-sectional shape. For laminar flow, β = 3.
For turbulent flow, under Manning friction: 1 ≤ β ≤ 5/3, depending on the shape
of the cross section. For turbulent flow, under Chezy friction: 1 ≤ β ≤ 3/2,
depending on the shape of the cross section.
What type of friction is described
by β = 2?
Mixed laminar-turbulent
(75% turbulent Manning), hydraulically wide.
For what condition can the value of β
be less than 1?
For a circular culvert flowing nearly full, β may actually attain values less than 1.
What is the Reynolds number?
The Reynolds number is the ratio of
diffusivity uoRo to kinematic viscosity ν.
What is the commonly
estimated range of Reynolds numbers for the
transitional regime in open-channel flow?
Transitional flow occurs in the
intermediate range: 500 < R ≤ 2000.
What is the dimensionless wavenumber?
The dimensionless wavenumber is the ratio
of hydraulic diffusivity and wave diffusivity.
Do kinematic waves attenuate?
Wave attenuation in a kinematic wave is theoretically zero.
Do dynamic waves attenuate?
Wave attenuation in a dynamic wave is theoretically zero.
Do mixed kinematic-dynamic waves attenuate?
Yes.
Which type of open-channel flow wave attenuates the most?
Mixed kinematic-dynamic waves.
For what value of dimensionless wavenumber
is the attenuation rate of mixed kinematic-dynamic waves
a maximum?
The attenuation rate is a maximum at the point of inflexion of the dimensionless celerity vs dimensionless wave number function.
What is the dimensionless
relative kinematic wave celerity under Chezy friction for a hydraulically wide channel?
0.5.
What is the characteristic reach length?
The characteristic reach length is the length
of channel in which the equilibrium flow drops a head equal to its depth.
What is the hydraulic diffusivity?
The hydraulic diffusivity is the product of
half of the velocity times the characteristic reach length.
For what value of channel slope is the
hydraulic diffusivity a maximum?
For channel slope equal to zero i.e., for a horizontal channel.
What is the dynamic hydraulic diffusivity?
The dynamic hydraulic diffusivity is the
product of the hydraulic diffusivity times (1 - V 2), where V is the
Vedernikov number.
Under what flow condition
does the dynamic hydraulic diffusivity vanish?
The dynamic hydraulic diffusivity vanishes for
V = 1.
In hydraulic engineering practice,
what does the term "dynamic wave" commonly refer to?
In hydraulic engineering practice,
the mixed kinematic-dynamic wave, which includes all the terms in the momentum
equation--friction, gravity, pressure gradient, and inertia--is commonly referred to as "dynamic wave."
What is the modified Darcy-Weisbach formula, applicable
to open-channel flow?
S =
f F 2
What is the typical range of Darcy-Weisbach friction factor
f in the turbulent range?
0.016 < f ≤ 0.036.
What is the typical range of the modified
Darcy-Weisbach friction factor f
in the turbulent range?
0.002 <
f ≤ 0.0045.
Is there a theoretical upper limit
to the Froude number? How can it be calculated?
About 25 to 30. It can be calculated by assumming a
maximum value of slope S and a
minimum value of f.
PROBLEMS
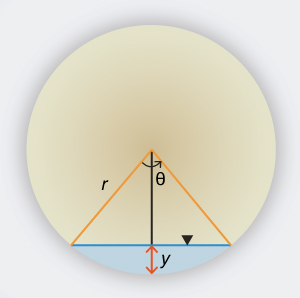
Derive the expression for the angle θ
in a circular channel (culvert) as a function of flow depth y and diameter
D, where D = 2r (Fig. 1-14).
Fig. 1-14 Definition sketch for a circular channel. cos [θ/2] = (r - y ) / r
θ = 2 cos-1 [(r - y ) / r ]
θ = 2 cos-1 [(1 - (y/r ) ]
θ = 2 cos-1 [(1 - 2 (y/D ) ]
Show that the maximum discharge
in a circular channel (Fig. 1-14)
is attained at y = 0.94 D. Use ONLINE CHANNEL 03.
Explain the reason for this behavior.
Use ONLINE CHANNEL 03 with any suitable data. From instance: D = 1 m; S = 0.01;
n = 0.025. Vary y between 0.9 and 0.99.
The maximum discharge Q = 2.232 m3/s is attained at y / D = 0.94.
The discharge is directly proportional to the flow area and inversely proportional
to the wetted perimeter. As y increases from 0.9 to 0.99, the wetted perimeter eventually increases at a faster rate than the area,
reducing the discharge. At y / D = 0.94, the discharge is a maximum.
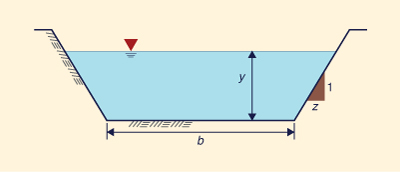
Derive the formula for flow area A,
wetted perimeter P, and top width T for
a trapezoidal channel, in terms of flow depth y,
bottom width b
and side slope z H: 1 V (Fig. 1-15).
Fig. 1-15 Definition sketch for a rectangular channel. A = 0.5 (b + b + 2zy) y = (b + zy) y
P = b + 2 y (1 + z 2)1/2
T = b + 2zy
Assume a trapezoidal channel of flow depth y, bottom width b,
and size slope z H: 1 V α = D / y
D = A / T
D = [( b + zy ) y ] / (b + 2zy )
α = D / y = ( b + zy ) / (b + 2zy )
α = [(b/y) + z ] / [(b/y) + 2z ]
b / y = z (1 - 2 α) / (α - 1)
For z = 1, and α = 0.99: b / y = 98 m.
Calculate the dimensionless
relative kinematic wave celerity under Manning friction for a hydraulically wide channel.
Q = (1/n) A R 2/3 S 1/2
Q = (1/n) A A 2/3 S 1/2 / P 2/3
Since the channel is hydraulically wide, the wetted perimeter is a constant.
Q = (1/n) P - 2/3 S 1/2 A 5/3
Q = α A β
β = 5/3
The dimensionless relative kinematic wave celerity is: β - 1 =
2/3.
What is the value of β for a hydraulically wide channel at Froude number β = 1 - (V / F) = 1 - (0.9 / 1.8) = 0.5
A hydraulically wide channel has flow depth = 1 m, and flow velocity = 1.5 m/s.
Calculate the Froude number. Confirm with ONLINE FROUDE.
V = u / (gh)1/2 = 1.5 / (9.806 × 1)1/2 = 0.479
Using ONLINE FROUDE: V = 0.479
A hydraulically wide channel has an exponent of the rating β = 1.6.
The flow depth is 1 m, and the flow velocity 1.5 m/s. Calculate the Vedernikov number. Confirm with ONLINE VEDERNIKOV.
V = (β - 1) u / (gh)1/2 = [ (1.6 - 1) × 1.5 ] / (9.806 × 1)1/2 = 0.287
Using ONLINE VEDERNIKOV: V = 0.287
Given a hydraulically wide channel with Manning friction, and
mean velocity u = 1 m/s, flow depth d = 1 m, and bottom slope S = 0.001. Determine
the kinematic and dynamic hydraulic diffusivities.
β = 5/3
νk = q / (2 So ) =
uh / (2 So ) = (1 × 1 ) / (2 × 0.001) = 500 m2/s
V = (β - 1) u / (gh)1/2 = [ (2/3) (1) ] / (9.806 × 1)1/2 = 0.2129
νd =
νk ( 1 - V 2 ) = 500 [1 - (0.2129)2 ] = 477.3 m2/s
Given a hydraulically wide channel with Chezy friction,
and flow depth d = 1 m.
What mean velocity will make the dynamic hydraulic diffusivity vanish?
β = 1.5
V = (β - 1) u / (gh)1/2 = 1
u = (gh)1/2 / (β - 1) = (9.806 × 1)1/2 / (0.5) = 6.263 m/s
According to the Blasius formula, what is the Reynolds number R
corresponding to a Darcy-Weisbach friction factor f = 0.03?
Using Eq. 1-25: R = 3053.
According to the Prandt-von Karman formula, what is the Reynolds number R
corresponding to a Darcy-Weisbach friction factor f = 0.03?
Using Eq. 1-27: R = 2807.
A WES spillway downstream slope is 0.6 H to 1 V.
The Darcy-Weisbach friction factor is S = 1 / 0.6 = 1.6667
f = 0.03 / 8 = 0.00375
F = (S / f )1/2 = 21.08
Assuming a maximum possible Froude number F = 25, calculate the value of
β that will
assure neutrally stable flow.
V = (β - 1) u / (gh)1/2 = (β - 1) F = 1
β - 1 = 0.04
β = 1.04
A prismatic channel is flowing close to critical flow.
The bottom slope is S = 0.004. What is the value of the Darcy-Weisbach's modified friction factor f?
f = S / F 2
F 2 ≅ 1
f ≅ 0.004
http://openchannelhydraulics.sdsu.edu
140819 09:30