|
|
| CAPÍTULO 1: INTRODUCCIÓN |
1.1 FLUJO EN CANALES ABIERTOS
|
|
El flujo en canales abiertos tiene una superficie libre y por lo tanto, está sujeto a la presión atmosférica (Fig. 1-1). Por el contrario, el flujo en conductos cerrados o tuberías, no tiene una superficie libre, estando sujeto solamente a una cierta presión hidráulica. Debido a su superficie libre, el análisis de flujo en un canal abierto es generalmente más complejo que la del flujo en un conducto cerrado. Es probable que la superficie libre varíe en el espacio y en el tiempo. Cuando la superficie libre varía en el espacio, el flujo se conoce como variado; cuando varía en el tiempo, se conoce como no permanente.
|
En el flujo en conductos cerrados, la sección transversal está fijada por las paredes internas de la tubería. Por otra parte, en el flujo de canales abiertos, la sección transversal no es fija, variando con el flujo. En el flujo en conductos cerrados, la rugosidad varía de latón suave a tuberías corroídas; en el flujo en canales abiertos, varía de vidrio acrílico (un tipo muy suave de plástico) a la de los cauces fluviales naturales y sus vecinas llanuras de inundación.
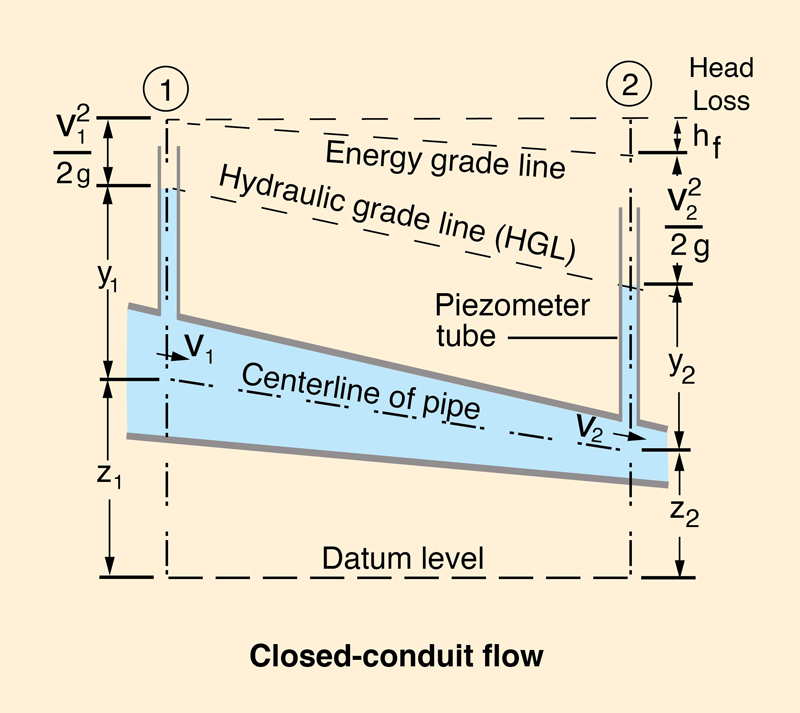
En el flujo en conductos cerrados, la presión hidráulica en el centro de la tubería define la línea de
gradiente hidráulico (HGL en la Fig. 1-2). La presión hidráulica (carga de agua) medida sobre la línea
central de la tubería se conoce como la carga piezométrica. La línea de la gradiente de energía
incluye la carga de velocidad
|
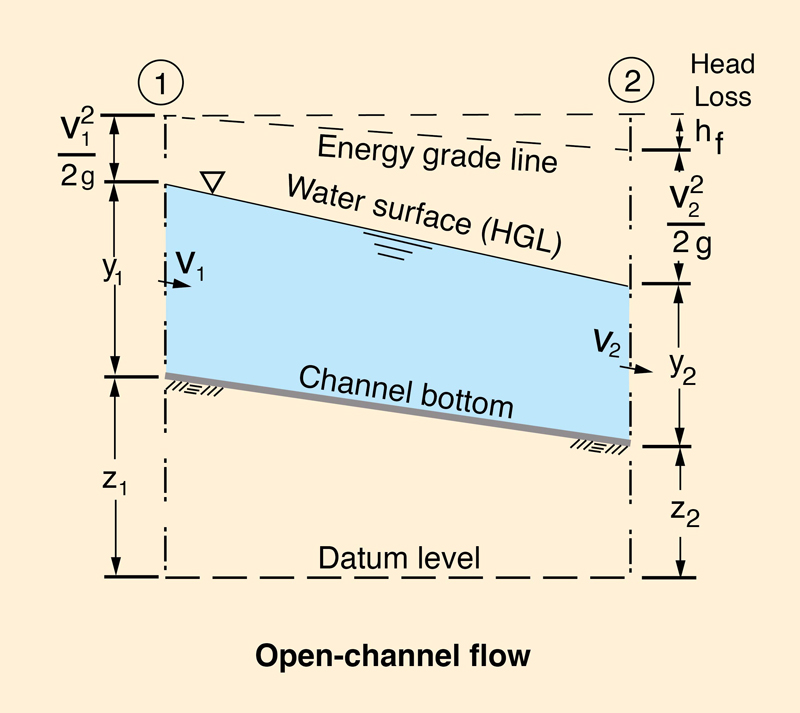
En el flujo de canal abierto, la profundidad de flujo medida sobre el fondo del canal define la elevación de la superficie del agua, la cual es equivalente a la línea del gradiente hidráulico del flujo en el conducto cerrado; ver Fig. 1-3. La carga total de la línea del gradiente de energía incluye la carga de velocidad
|
Existe una diferencia entre el flujo en conductos cerrados y el flujo en canales abiertos. En el flujo en un conducto cerrado, el agua se elevará en el tubo piezométrico hasta el nivel donde éste defina la línea del gradiente hidráulico asociada con la presión hidráulica en el conducto. Adicionalmente, en el flujo en un canal abierto, la superficie del agua es la línea del gradiente hidráulico, la cual se encuentra a presión atmosférica.
1.2 TIPOS DE FLUJO
|
|
Existen dos tipos de secciones transversales en un canal:
- Prismática, y
- No prismática.
Los canales artificiales son por lo general prismáticos, de forma y tamaño constantes a lo largo de gran parte de la longitud del canal. Por el contrario, los canales naturales son generalmente no prismáticos, es decir, la forma y tamaño de la sección transversal varían a lo largo del canal. A los canales artificiales se les conoce simplemente como canales.
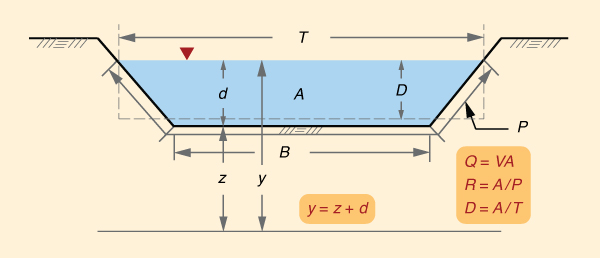
Varias propiedades geométricas e hidráulicas ayudan a describir un canal (Fig. 1.4). Éstas son:
- Flujo o caudal Q,
- Área de flujo A,
- Velocidad media V, en la cual V = Q /A,
- Perímetro mojado P,
- Ancho de la superficie libre T,
- Radio hidráulico R, en el cual R = A /P,
- Profundidad hidráulica D, en la cual D = A /T,
- Ancho del fondo del canal B,
- Elevación del fondo del canal z,
- Tirante, profundidad o calado d,
- Altura total o elevación de la superficie libre, en la cual y = z + d.
|
En los canales prismáticos, el tirante d generalmente se describe como y, particularmente cuando no se puede confundir con la elevación de la superficie libre (sobre el datum). Además, el talud del canal se describe como z H: 1 V, particularmente cuando no se puede confundir con la elevación del fondo del canal.
Clasificación del flujo en canales
El flujo en canales abiertos se puede clasificar como sigue:
- Estable o inestable.
- Uniforme o en equilibrio.
- Gradualmente variado o rápidamente variado.
- Espacialmente variado.
El flujo es estable cuando las variables hidráulicas (flujo, área de flujo, velocidad media, profundidad del flujo, etc.) no varían con el tiempo. Por el contrario, el flujo es inestable cuando las variables hidráulicas varían con el tiempo y espacio. El flujo estable es relativamente más sencillo de calcular que el flujo inestable.
El flujo es uniforme cuando el canal es prismático y las variables hidráulicas (Q, A, V, d, etc.) son constantes en el tiempo y en el espacio. El flujo está en equilibrio cuando el canal es no prismático y las variables hidráulicas son aproximadamente constantes en el tiempo y espacio. El cálculo del flujo uniforme es relativamente sencillo en comparación con el de otros estados de flujo.
El flujo es gradualmente variado cuando la descarga Q es constante pero las otras variables hidráulicas (A, V, d, etc.) varían gradualmente en el espacio. En el flujo gradualmente variado, la distribución de presión en la dirección vertical, normal al flujo, se aproxima a la hidrostática, es decir, es proporcional a la profundidad de flujo.
El flujo es rápidamente variado cuando la descarga es constante pero las otras variables hidráulicas (A, V, d, etc.) varían rápidamente en el espacio. Por lo tanto, no es posible asumir la presión hidrostática en la dirección vertical. El cálculo del flujo gradualmente variado es complicado pero factible, mientras que el cálculo del flujo rápidamente variado es generalmente más complejo, y está basado en fórmulas empíricas, a falta de una solución teórica.
El flujo es espacialmente variado cuando la descarga Q varía en el espacio solamente, es decir, a lo largo del canal. Generalmente, dicha variación se debe a la entrada o salida lateral de flujo.
Acontecimiento de diferentes tipos de flujo
El flujo uniforme ocurre en un canal prismático (Fig 1-5); el flujo en equilibrio estable ocurre en un canal no prismático. El flujo uniforme inestable no existe en la naturaleza, ya que el flujo no puede ser uniforme y variable al mismo tiempo. La palabra "inestable" implica no equilibrio; por lo tanto, no existe flujo en equilibrio inestable.
|
El flujo gradualmente variado se define por medio de perfiles de la superficie del agua; a estos perfiles también se les conoce como perfiles de remanso (Capítulo 7). El flujo no permanente gradualmente variado es el cálculo de los flujos de inundación, o tránsito de avenidas (Capítulo 10).
El flujo permanente rápidamente variado está representado por el flujo sobre vertederos o el resalto hidráulico. Mientras que el flujo no permanente rápidamente variado está representado por el resalto hidráulico en movimiento, marejadas, ondas de rollo, choques cinemáticos y grandes olas de marea. La Figura 1-6 muestra un tren de ondas de rollo en un canal de riego de pendiente pronunciada.
El flujo espacialmente variado ocurre cuando el caudal varía a lo largo del canal, debido a extracciones laterales o desbordamientos.
|
1.3 ESTADO DE FLUJO
|
|
El estado de flujo de un canal puede ser descrito en base a ciertas velocidades y viscosidades características.
La velocidad es la relación de la longitud (distancia) sobre el tiempo, con unidades
Relaciones de velocidad
Existen tres velocidades características en el flujo en canales:
-
La velocidad media u del flujo uniforme;
La velocidad, o celeridad ck de las ondas cinemáticas; y
- La velocidad, o celeridad (en realidad, dos celeridades) cd de las ondas dinámicas.
La velocidad media del flujo uniforme se define usando la ecuación de Manning (unidades SI):
|
1 u = _____ R 2/3 S 1/2 n | (1-1) |
en la que n = coeficiente de fricción de Manning, R = radio hidráulico, y S = pendiente de fricción.
Con la ecuación de Chezy, la velocidad media del flujo uniforme es:
|
u = C R 1/2 S 1/2 | (1-2) |
en la que C = coeficiente de Chezy.
El control de volumen de flujo en canales está sujeto a cuatro fuerzas: fricción, gravedad, gradiente de presión o profundidad de flujo, e inercia. Las ondas cinemáticas son aquéllas donde el balance de momento es expresado en base a las fuerzas de fricción y de gravedad solamente (Lighthill y Whitham, 1955).
La celeridad de las ondas cinemáticas o celeridad de Seddon, es (Seddon, 1990; Chow, 1959; Ponce, 1989):
|
ck = β u | (1-3) |
en la cual β = exponente de la relación entre área de flujo y descarga, y se muestra como sigue:
|
Q = α Aβ | (1-4) |
Las ondas dinámicas son aquéllas para las cuales el balance de momento se define en base al gradiente de presión y las fuerzas de inercia solamente. La celeridad de las ondas dinámicas se expresa como sigue:
|
cd = u ± (g D )1/2 | (1-5) |
en la cual g = aceleración de la gravedad, y D = profundidad hidráulica, D = A /T.
De la Ec. 1-3, la celeridad relativa de las ondas cinemáticas se expresa como sigue:
|
v = (β - 1) u | (1-6) |
De la Ec. 1-5, el valor absoluto de la celeridad relativa de ondas dinámicas se expresa como sigue:
|
w = (g D )1/2 | (1-7) |
En canales rectangulares, donde D = d, o en canales hidráulicamente anchos, donde D ≅ d, la celeridad relativa de ondas dinámicas es:
|
w = (g d )1/2 | (1-8) |
La Ec. 1-8 es la celeridad relativa de Lagrange, en honor a Lagrange (1788), quien fue el primero en derivarla.
Número de Froude
El número de Froude se define como sigue (Chow, 1959):
|
u F = _____ w | (1-9) |
El número de Froude clasifica a las siguientes condiciones de flujo:
- F < 1: Flujo subcrítico, o u < w,
- F = 1: Flujo crítico, o u = w,
- F > 1: Flujo supercrítico, o u > w.
En el flujo subcrítico, las ondas superficiales (perturbaciones) pueden trasladarse aguas arriba, ya que la celeridad -w es mayor que la velocidad media del flujo u.
En el flujo crítico, las ondas superficiales (perturbaciones) permanecen estacionarias, ya que su celeridad (absoluta) w es igual a la velocidad media del flujo u.
En el flujo supercrítico, las ondas de superficiales (perturbaciones) pueden trasladarse únicamente aguas abajo, debido a que su celeridad -w es menor que la velocidad media del flujo u.
El Número de Vedernikov
El número de Vedernikov se define como sigue (Vedernikov, 1945; 1946; Powell, 1948; Craya, 1952):
|
v V = _____ w | (1-10) |
El número Vedernikov clasifica a los siguientes estados de flujo:
- V < 1: Flujo estable, donde v < w,
- V = 1: Flujo neutralmente estable , donde v = w,
- V > 1: Flujo inestable, donde v > w.
En el flujo estable, la celeridad relativa de la onda cinemática v es menor que la celeridad relativa de la onda dinámica w, por lo tanto, las ondas superficiales (perturbaciones) tienen la capacidad de disipación.
En el flujo neutralmente estable, la celeridad relativa de la onda cinemática v es igual a la celeridad relativa de la onda dinámica w; por lo tanto, las ondas superficiales (perturbaciones) no se atenúan ni se amplifican. La amplificación y la disipación se cancelan mutuamente.
En el flujo inestable, la celeridad relativa de la onda cinemática v es mayor que la celeridad relativa de la onda dinámica w. Por lo tanto, las ondas superficiales (perturbaciones) tienden a amplificarse. En la práctica, la condición V ≥ 1 conduce al desarrollo de las ondas de rollo, un tren de ondas que viajan aguas abajo, generalmente en los canales de pendiente pronunciada (Cornish, 1907) (Fig. 1-7).
|
| ||||
|
William Froude nació en Dartington, Devon, Inglaterra el 28 de Noviembre de 1810 y murió
de un derrame cerebral en un crucero en Simonstown, Sudáfrica a los 69 años. A lo largo de su vida fue
ingeniero,
hidrodinamicista y arquitecto naval.
Adquirió su formación en matemáticas en Oxford en 1832. Inmediatamente después de
su graduación,
trabajó como topógrafo para Isambard Kingdom Burnel, el afamado empresario de ferrocarriles,
en el Great Western
Railway, en Inglaterra.
En 1857, Brunel le pidió asistencia para mejorar el comportamiento de la nave Great Eastern en altamar.
Siguiendo las sugerencias de Froude, Brunel modificó el diseño de la nave para minimizar el
movimiento de volteo.
A partir de 1859, Froude construyó el primer tanque de remolque, utilizando sus propios recursos.
Además,
llevó
a cabo experimentos de modelos de barcos en dicho tanque. Inició este trabajo
en su casa en
Paignton
y posteriormente trabajó en su otra casa, ubicada en Torquay, llamada Chelston Cross.
En 1861, Froude escribió un artículo sobre el diseño de la estabilidad de los barcos.
El artículo fue publicado en las Actas de la Institución de Arquitectos Navales. Posteriormente,
entre 1863 y 1867, Froude demostró que la escala entre modelo y prototipo (el buque real) se puede aplicar
(es decir, la resistencia de fricción es igual) cuando la velocidad (V)
es proporcional a la raíz cuadrada de la longitud (L). A este concepto
le llamó la "Ley de Comparación."
V = k (L)1/2
en la cual k es el número que se aplica tanto al modelo como al prototipo.
Esta
ley se conoce como la ley de Froude, a pesar de que él mismo reconoció que Ferdinand Reech
(1805-1850)
presentó el mismo concepto veinte años antes.
El trabajo de Froude fue inovador ya que fue el primero en identificar la forma física de mayor eficiencia
para cascos de
los barcos. Además, pudo predecir la estabilidad de buques en base a modelos a escala reducida.
En la hidráulica de canales, la ley de Froude se expresa en términos del número de Froude:
F = V / (gD) 1/2
en la cual V = velocidad media, D = profundidad
hidráulica, y g = aceleración de la gravedad.
A diferencia de la relación original (k), el número de Froude
F es adimensional.
La L ha sido reemplazada por D para
representar
de mejor manera la fuerza de gravedad en el flujo.
|
El exponente β de la relación descarga-área
Las tres velocidades u, v, y w conducen a dos relaciones independientes de velocidad, los números de Froude (Eq. 1-8) y Vedernikov (Eq. 1-9). La tercera relación:
|
v
V β - 1 = _____ = _____ u F | (1-11) |
se conoce como la celeridad relativa adimensional de la onda cinemática, la cual es equivalente al exponente de la relación descarga-área menos 1. Por lo que el exponente β de la Ec. 1-4 es una función de ambos números: el de Froude y el de Vedernikov.
El valor de β varía tanto con el régimen de fricción (laminar, transicional, o turbulento; y Manning o Chezy turbulentos) como con la forma de la sección transversal. Para el flujo laminar, β = 3. Para el flujo turbulento con la fricción de Manning: 1 ≤ β ≤ 5/3, dependiendo de la forma de la sección transversal. Para flujo turbulento con la fricción de Chezy: 1 ≤ β ≤ 3/2, dependiendo de la forma de la sección transversal.
Tipos de secciones transversales
Existen tres tipos asintóticos de secciones transversales de canales:
-
El canal hidráulicamente ancho, para el cual el perímetro mojado P es una constante (Ponce y Porras, 1995). En este caso,
β = 5/3 para la fricción de Manning, y β = 3/2 para la fricción de Chezy. Se considera que una sección transversal es hidráulicamente ancha cuando la relación entre el ancho de superficie y la profundidad de flujoT /d > 10. En la práctica, la mayoría de los canales naturales son hidráulicamente anchos (Fig. 1-8).
Nuccitelli Fig. 1-8 Río Mississippi en Mud Island, Memphis, Tennessee.
-
El canal triangular, para el cual el ancho de superficie T es proporcional a la profundidad de flujo d (Fig. 1-9). Para la fricción de Manning,
β = 4/3 , y para la fricción de Chezy, β = 5/4. El drenaje de carreteras (canaletas) con frecuencia se hace con secciones transversales triangulares.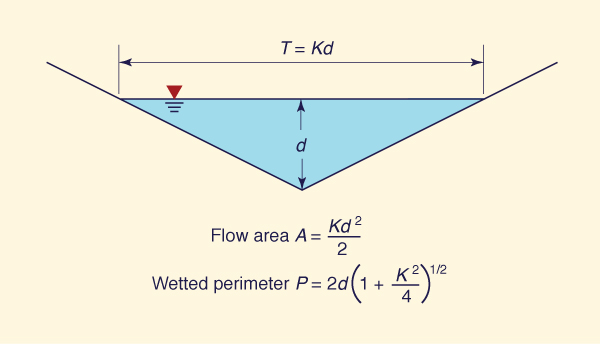
Fig. 1-9 Definición de una sección triangular transversal.
-
El canal inherentemente estable, para el cual el radio hidráulico R es una constante (Ponce y Porras, 1995). En este caso, β ≡ 1 (Fig. 1-10).
Fig. 1-10 Un canal inherentemente estable.
Flujo neutralmente estable
Para la estabilidad neutral: V = 1. Por lo tanto, de acuerdo con la Ec. 1-11, el número de Froude correspondiente al flujo neutralmente estable es:
|
1 Fns = ________ β - 1 | (1-12) |
La Tabla 1-1 muestra los valores de Fns para ciertos valores de β. Es posible observar como β varía de β = 3 (flujo laminar) a β = 1 (sección inherentemente estable), los valores de Fns varían de Fns = 1/2 a Fns = ∞. En otras palabras, cuando β ⇒ 1, Fns ⇒ ∞.
En la práctica, la fricción tiene un límite inferior. Por lo tanto, el número de Froude tiene un limite superior de F = 25. En la mayoría de los casos, un valor de β = 1.04 sería ya estable para fines prácticos.
| Tabla 1-1 Valores de Fns para valores seleccionados de β. | |||
| β | Tipo de flujo | Forma de la sección transversal | Fns |
| 3 | Laminar | Hidráulicamente ancha | 1/2 |
| 8/3 | Laminar-turbulento mixto (Manning 25% turbulento) |
Hidráulicamente ancha | 3/5 |
| 21/8 | Laminar-turbulento mixto (Chezy 25% turbulento) |
Hidráulicamente ancha | 8/13 |
| 7/3 | Laminar-turbulento mixto (Manning 50% turbulento) |
Hidráulicamente ancha | 3/4 |
| 9/4 | Laminar-turbulento mixto (Chezy 50% turbulento) |
Hidráulicamente ancha | 4/5 |
| 2 | Laminar-turbulento mixto (Manning 75% turbulento) |
Hidráulicamente ancha | 1 |
| 15/8 | Laminar-turbulento mixto (Chezy 75% turbulento) |
Hidráulicamente ancha | 8/7 |
| 5/3 | Manning turbulento | Hidráulicamente ancha | 3/2 |
| 3/2 | Chezy turbulento | Hidráulicamente ancha | 2 |
| 4/3 | Manning turbulento | Triangular | 3 |
| 5/4 | Chezy turbulento | Triangular | 4 |
| 1 | Cualquiera | Inherentemente estable | ∞ |
Como se muestra en la Tabla 1-1, los valores de β para canales y para flujo laminar se limitan
a un rango entre
Relaciones de viscosidad
Existen tres clasificaciones para viscosidades de flujo en canales:
La viscosidad interna, o viscosidad cinemática ν del fluído (Apéndice A),
La viscosidad externa (o difusividad hidráulica νh) del flujo permanente; y
La viscosidad externa (o difusividad de onda νw) del flujo transitorio.
La viscosidad cinemática ν del fluido varía en función de la temperatura (Apéndice A).
El concepto de difusividad hidráulica νh se debe a Hayami (1951). Hayami combinó las ecuaciones que rigen el comportamiento del flujo en canales abiertos (Capítulo 10) para desarrollar una ecuación de convección-difusión única. Es decir, una ecuación que describe la convección (un proceso de primer orden) y difusión (un proceso de segundo orden) de una onda de avenida. La difusividad hidráulica se define como sigue:
|
qo νh = _______ 2 So | (1-13) |
en la cual qo = descarga de equilibrio, por unidad de ancho, y So = pendiente de fricción (energía). La difusión de la onda de avenida es directamente proporcional a la descarga de equilibrio unitaria e inversamente proporcional a la pendiente de fricción.
La ecuación 1-13 se expresa en términos de la velocidad y la profundidad del flujo como sigue:
|
uo do νh = _________ 2 So | (1-14) |
Un valor relacionado a la difusividad pero independiente de la pendiente es:
|
νh' = uo do | (1-15) |
Por lo general, para cualquier forma de sección transversal:
|
νh' = uo Ro | (1-16) |
en la cual Ro = radio hidráulico.
En la teoría de la onda cinemática, la longitud característica de tramo se define de la siguiente manera (Lighthill and Whitham, 1955):
|
do Lo = ______ So | (1-17) |
en la que Lo es la longitud del canal en la que el flujo de equilibrio tiene una caída equivalente a su profundidad. Por lo tanto, en términos de la longitud característica de tramo, la difusividad hidráulica es:
|
uo Lo νh = _______ 2 | (1-18) |
De manera semejante a la difusividad hidráulica, la difusividad de onda se define como sigue:
|
uo L νw = _______ 4 π | (1-19) |
en la cual L = longitud de onda.
El Número de Reynolds
El número de Reynolds R es (Chow, 1959):
|
vh' uo Ro R = ______ = ________ ν ν | (1-20) |
El número de Reynolds R clasifica al régimen de flujo en:
- Laminar,
- Transicional, o
- Turbulento.
Bajo condiciones de flujo permanente en un canal, el flujo laminar
está representado por R ≤ 500 y el flujo turbulento con R > 2000. El flujo de
transición está representado por el rango intermedio:
En la práctica, la mayoría de los casos de flujo en canales se encuentran sujetos a un régimen turbulento. Por el contrario, la mayoría de los casos de flujo en planos de superficie libre se encuentran bajo régimen laminar o laminar-turbulento mixto.
El número de onda adimensional
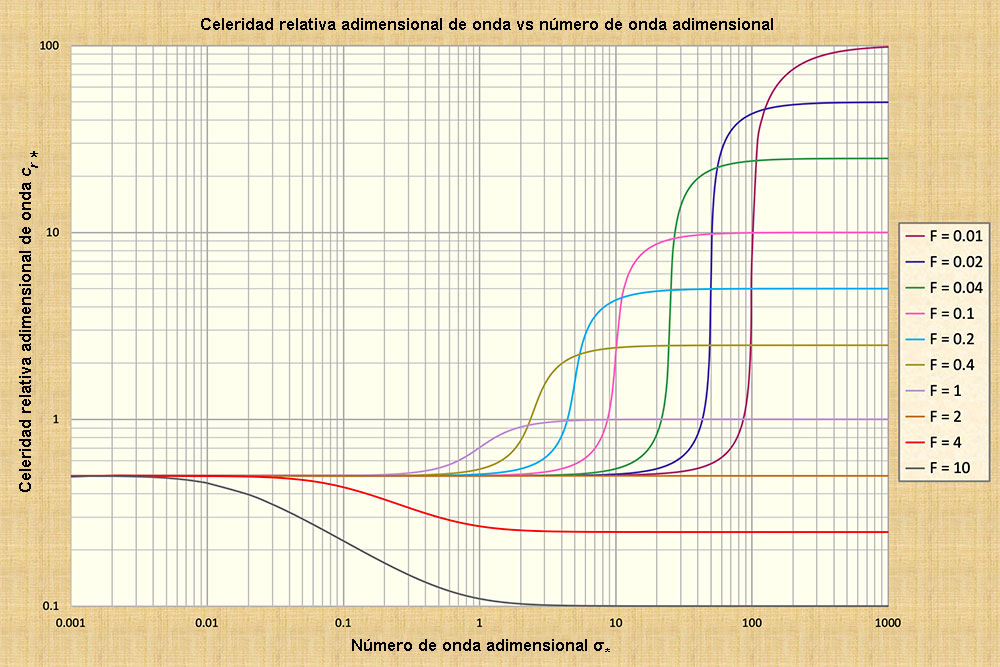
El número de onda adimensional σ se define como sigue (Ponce and Simons, 1977):
|
νh 2 π σ = ______ = _____ Lo νw L | (1-21) |
El número de onda σ describe la escala adimensional de longitud de onda, como se muestra en la Fig. 1-11, en términos de: (a) ondas cinemáticas, (b) ondas dinámicas, y (c) ondas cinemáticas-dinámicas combinadas. La Figura 11 es aplicable a la fricción de Chezy en los canales hidráulicamente anchos.
Bajo flujo cinemático, el cual se muestra en el lado izquierdo de la Fig. 1-11:
-
El balance de momento se describe en términos de las fuerzas de fricción y de gravedad únicamente,
-
Prevalece la celeridad adimensional de onda cinemática relativa (Ec. 1-3), la cual es una constante para todos los números de onda y de Froude, y
-
La atenuación de la onda es teóricamente cero.
Bajo flujo dinámico, el cual se muestra en el lado derecho de la Fig. 1-11:
El balance de momento se describe en términos del gradiente de presión e inercia, únicamente,
Prevalece la celeridad adimensional de onda dinámica relativa (Ec. 1-5), la cual es una constante para todos los números de onda, y variable con el número de Froude, y
La atenuación de la onda es teóricamente cero.
Bajo el flujo cinemático-dinámico mixto, el cual se muestra en la sección central de la Fig. 1-11:
El balance de momento incorpora las cuatro fuerzas presentes en el flujo transitorio en canales (fricción, gravedad, gradiente de presión, e inercia),
No hay celeridad característica, por lo que la onda se encuentra sujeta a una atenuación muy fuerte dentro del rango medio de números de onda adimensionales, y
Para cada curva que se muestra en la Fig. 1-11, el punto de inflexión representa la attenuación máxima (Ver el Capítulo 10) (Ponce y Simons, 1977).
|
Difusividad hidráulica dinámica
La difusividad hidráulica dinámica considera el balance de momento completo (Dooge et al., 1982;
Ponce, 1991a; 1991b), a diferencia de la
difusividad hidráulica de Hayami,
|
uo Lo νh = _______ (1 - V 2) 2 | (1-22) |
Para números de Vedernikov bajos, V ⇒ 0, la difusividad hidráulica dinámica se reduce a la difusividad hidráulica cinemática, es decir, la Ec. 1-18. Por el contrario, en los casos donde los números de Vedernikov sean altos, V ⇒ 1, la difusividad hidráulica dinámica se desvanece por completo. La ausencia total de la atenuación de la onda conduce al desarrollo de las ondas de rollo (Figs. 1-6 and 1-7).
|
Nota de precaución en base al uso del término de "onda dinámica"
En la práctica de la ingeniería hidráulica, la onda cinemática-dinámica mixta,
la cual incluye todos los términos de la ecuación de momento - la fricción, la gravedad, la gradiente
de presión, y la inercia - se conoce como "onda-dinámica," de acuerdo a Fread
(1993). Sin embargo, la onda dinámica original de Lagrange (1788) considera sólo la gradiente
de presión y la inercia. Para añadir a la confusión, a la onda dinámica de Lagrange se le
conocetambién como
"onda de gravedad." El término "onda de gravedad" no es apropiado, ya que la fuerza
de gravedad está claramente ausente de su formulación.
Por lo tanto, es preferible reservar el término "cinemática" para las ondas que se rigen por la
fricción y la gravedad (de acuerdo a Lighthill y Whitham), y "dinámica" para las ondas que se rigen por
el gradiente de presión y la inercia (de acuerdo a Lagrange). El término "cinemático-dinámico mixto" se debe utilizar únicamente para las ondas que se rigen por todos los términos de la ecuación de momento (las cuatro fuerzas).
|
1.4 REGÍMENES DE FLUJO
|
|
Los regímenes de flujo en canales son:
- Laminar,
- Transicional, y
- Turbulento.
Los regímenes de flujo se caracterizan por el número de Reynolds R, Ec. 1-20. En el flujo en canales, el régimen laminar prevalece cuando R ≤ 500, el régimen transicional cuando 500 < R ≤ 2000, y el régimen turbulento cuando R > 2000.
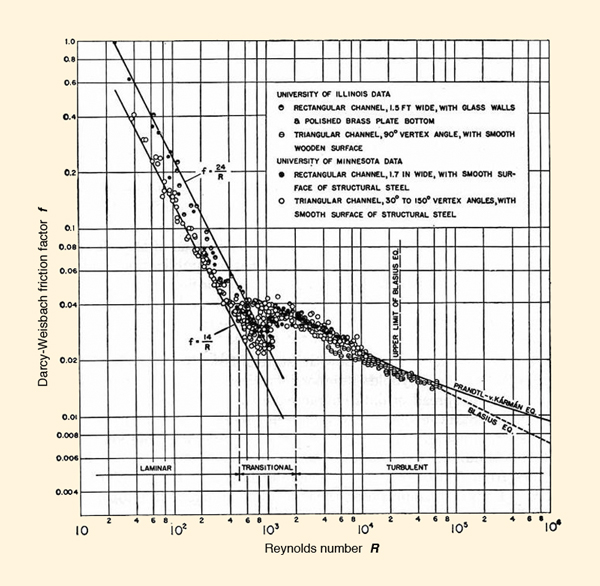
Los regímenes de flujo varían de acuerdo a la rugosidad de la superficie del canal. La Figura 1-12 muestra la relación entre el número de Reynolds R y el factor de fricción de Darcy-Weisbach f para el flujo en canales lisos. La Figura 1-13 muestra la relación entre el número de Reynolds R y el factor de fricción para el flujo en canales rugosos.
La fórmula de fricción de Darcy-Weisbach, desarrollada para el flujo en tuberías, es:
|
L
V 2 hf = f _____ ______ do 2 g | (1-23) |
en la cual hf = pérdida de carga por fricción; f = factor de fricción de Darcy-Weisbach; L = longitud de la tubería; do = diámetro de la tubería; V = velocidad media de flujo; y g = aceleración de la gravedad
|
|
El estudio de las Figuras 1-12 y 1-13 permite las siguientes conclusiones:
-
El flujo laminar prevalece cuando los números de Reynolds son bajos. En estos casos, el factor de fricción de Darcy-Weisbach es inversamente proporcional al número de Reynolds. Por lo general:
K
f = _____
R(1-24) en la cual K es una constante que varía entre 14 (para canales triangulares) y 24 (para canales rectangulares, para superficies de canales lisos; y entre 33 y 60 para las superficies de canales rugosos.
El rango transicional no está bien definido, ya que depende hasta cierto punto de la forma del canal. Para fines prácticos, se puede suponer que el rango transicional para el flujo en canales es:
500 ≤ R ≤ 2000. En el flujo turbulento, la relación entre f y R sigue la fórmula de Blasius (Chow, 1959):
0.223
f = _________
R 0.25(1-25) Esta ecuación es válida para números de Reynolds en el rango: 750 ≤ R ≤ 25,000.
Una expresión general para la relación entre f and R fue desarrollada por von Karman y posteriormente modificada por Prandlt. La ecuación de Prandtl-von Karman es (Chow, 1959):
1
_______ = 2 log (R f 1/2 ) + 0.4
f 1/2(1-26)
Nótese que la ecuación de Prandtl-von Karman se puede expresar en forma explícita de la siguiente manera:
|
1 R = _______ 10 [ ( 1 - 0.4 f 1/2 ) / ( 2 f 1/2 ) ] f 1/2 | (1-27) |
El factor de fricción de Darcy-Weisbach para el flujo en canales
La fórmula de Darcy-Weisbach, Ec. 1-23, es de uso exclusivo para el flujo de conducto cerrado (tubería). Para el flujo en tuberías, la longitud de fricción característica es el diámetro do. Por otro lado, para el flujo en canales, la longitud de fricción característica es el radio hidráulico R, es decir, la relación de área de flujo al perímetro mojado:
|
A R = ______ P | (1-28) |
Dado que el área de flujo de un tubo circular (que fluye lleno) es A = π do2/4, y el perímetro mojado es P = π do, se deduce que el radio hidráulico es igual a 1/4 del diámetro del tubo o, a la inversa, que el diámetro es igual a 4 veces el radio hidráulico. Por lo tanto, la fórmula de Darcy-Weisbach aplicable al flujo en canales es:
|
L
V 2 hf = f ______ ______ 4R 2g | (1-29) |
en la cual V = velocidad media del flujo.
La pendiente de la línea de energía en el flujo en canales es la misma que la pendiente de fricción, del lecho o del fondo, cuando se encuentra bajo flujo permanente. Se expresa como sigue:
|
hf
V 2 f V 2 S = ______ = f _______ = ___ _______ L 8gR 8 gR | (1-30) |
Para una sección transversal arbitraria, el número de Froude es:
|
V F = __________ (gD)1/2 | (1-31) |
en la cual D = profundidad hidráulica: D = A /T.
La ecuación 1-30 se puede expresar en términos del número de Froude como sigue:
|
f D S = ___ _____ F 2 8 R | (1-32) |
La Ecuación 1-32 establece la proporcionalidad entre la pendiente de la línea de energía y el número de Froude. El factor de proporcionalidad es función del factor de fricción de Darcy-Weisbach y el factor de forma D /R.
Para un canal hidráulicamente ancho, para el cual D ≅ R, la Ec. 1-32 se reduce a:
|
f S = ___ F 2 8 | (1-33) |
Para el caso de un canal hidráulicamente ancho, el factor de proporcionalidad entre la pendiente de la línea de energía y el número de Froude es solamente una función del factor de fricción de Darcy-Weisbach. Por convenciencia, para el flujo en canales se puede utilizar un factor de fricción modificado de Darcy-Weisbach f, igual a 1/8 del factor de fricción convencional. La ecuación modificiada de Darcy-Weisbach para el flujo en canales es:
|
S = f F 2 | (1-34) |
La Tabla 1-2 muestra los valores aproximados del factor de fricción Darcy-Weisbach f y el factor de fricción modificado f correspondiente para valores seleccionados de R en el rango turbulento.
| Tabla 1-2 Valores aproximados de factores de fricción
f y f para valores seleccionados de R en el rango turbulento. |
||
| R | f | f |
| 2000 | 0.036 | 0.0045 |
| 4000 | 0.032 | 0.004 |
| 7000 | 0.028 | 0.0035 |
| 10000 | 0.024 | 0.003 |
| 15000 | 0.020 | 0.0025 |
| 60000 | 0.016 | 0.002 |
|
La proporcionalidad entre la pendiente de energía y el número de Froude
La Ecuación 1-33 muestra una propiedad fundamental del flujo en canales abiertos en el rango turbulento: La
proporcionalidad entre la pendiente de la línea de energía y el número de Froude. Las relaciones siguientes
son válidas:
Cuando la f es constante, un aumento en la pendiente de la línea de energía S
aumentará proporcionalmente el número de Froude
F, y viceversa.
Cuando la F es constante,
un aumento en la pendiente de la línea de energía S aumentará proporcionalmente el factor de fricción f, y viceversa.
Cuando la S es constante,
un aumento en el número de Froude F disminuirá proporcionalmente el factor de fricción
f, y viceversa.
|
PREGUNTAS
|
|
-
¿Cuál es la diferencia entre la profundidad de flujo d y la profundidad hidráulica D?
-
¿Es posible un flujo uniforme transitorio? ¿Por qué no?
-
¿Cuáles son las cuatro fuerzas que actúan en el balance de momento en el flujo en canales?
-
¿Qué es una onda cinemática?
-
¿Qué es una onda dinámica según Lagrange?
-
¿Cuál es la definición del número de Froude?
-
¿Cuál es la definición del número de Vedernikov?
-
¿Qué es el flujo neutralmente estable?
-
¿Cuál es el rango normal del exponente β para el flujo en canales y superficial?
-
¿Qué tipo de fricción es descrita por un valor β = 2?
-
¿Bajo que condición puede ser el valor de β menor que 1?
-
¿Cuál es la definición del número de Reynolds?
-
¿Cuál es el rango común para el número de Reynolds en el régimen transicional del flujo en canales?
-
¿Qué es el número de onda adimensional?
-
¿Las ondas cinemáticas se atenúan?
-
¿Las ondas dinámicas se atenúan?
-
¿Las ondas cinemáticas-dinámicas mixtas se atenúan?
-
¿Qué tipo de ondas en el flujo en canal se atenúa más?
-
¿Bajo qué valor de número de onda adimensional la tasa de atenuación de las ondas cinemáticas-dinámicas mixtas alcanza su valor máximo?
-
¿Cuál es la celeridad de onda cinemática relativa adimensional aplicable para la fricción de Chezy para un canal hidráulicamente ancho?
-
¿Cuál es la longitud característica de tramo?
-
¿Qué es la difusividad hidráulica?
-
¿Para qué valor de pendiente del fondo la difusividad hidráulica es máxima?
-
¿Qué es la difusividad hidráulica dinámica?
-
¿Bajo qué condición de flujo desaparece la difusividad hidráulica dinámica?
-
En la práctica de la ingeniería hidráulica, a qué se refiere el término "onda dinámica"?
-
¿Cuál es la fórmula modificada de Darcy-Weisbach modificada, aplicable al flujo en canales?
-
¿Cuál es el rango típico del factor de fricción de Darcy-Weisbach f en el rango turbulento?
-
¿Cuál es el rango típico del factor de fricción modificado de Darcy-Weisbach f en el rango turbulento?
-
¿En teoría, existe un límite superior para el número de Froude? ¿Cómo se puede calcular?
PROBLEMAS
|
|
-
Derive la expresión para el ángulo θ en un canal circular, en función de la profundidad de flujo y y el diámetro D, en la cual D = 2r (Fig. 1-14).
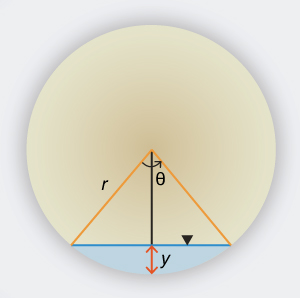
Fig. 1-14 Definición de un canal circular.
-
Demuestre que la descarga máxima en un canal circular (Fig. 1-14) se obtiene para y = 0.94 D. Utilice ONLINE CHANNEL 03. Explique la razón de este comportamiento.
-
Derive la fórmula para el área de flujo A, perímetro mojado P, y el ancho de superficie T para un canal trapezoidal, en términos de la profundidad de flujo y, el ancho de fondo b y la pendiente lateral z H: 1 V (Fig. 1-15).
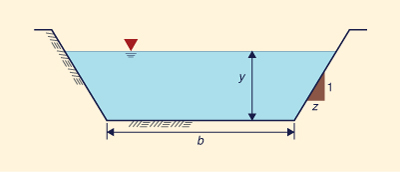
Fig. 1-15 Definición de un canal trapezoidal.
-
Asuma un canal trapezoidal de profundidad de flujo y, ancho de fondo b, y la pendiente lateral
z H: 1 V ¿Qué velocidad media hará que la difusividad hidráulica dinámica desaparezca?(Fig. 1-15). Derive una expresión para la relación ancho-profundidad b/y en función de α, la relación de la profundidad hidráulica D a la profundidad de flujo y. Dado z = 1, y α = 0.99, ¿Cuál es el valor de b/y?Calcule la celeridad relativa adimensional de la onda cinemática aplicable a la fricción de Manning en un canal hidráulicamente ancho.
¿Cuál es el valor de β para un canal hidráulicamente ancho cuando el número de Froude
F = 1.8 y el número de Vedernikov V = 0.9?Un canal hidráulicamente ancho tiene una profundidad de flujo de 1 m, y velocidad de flujo de 1.5 m/s. Calcule el número de Froude. Confirme con ONLINE FROUDE.
Un canal hidráulicamente ancho tiene un exponente de la curva de gasto β = 1.6. La profundidad de flujo es de 1 m, y la velocidad de flujo 1.5 m/s. Calcule el número de Vedernikov. Confirme con ONLINE VEDERNIKOV.
Dado un canal hidráulicamente ancho bajo la fricción de Manning, con velocidad media u = 1 m/s, profundidad de flujo d = 1 m, y la pendiente de fondo S = 0.001. Determine las difusividades hidráulicas cinemáticas y dinámicas.
Dado un canal hidráulicamente ancho con fricción de Chezy y profundidad de flujo d = 1 m.
-
De acuerdo a la fórmula de Blasius, ¿Cuál es el número de Reynolds R que corresponde a un factor de fricción de Darcy-Weisbach f = 0.03?
-
De acuerdo a la fórmula de Prandt-von Karman, ¿Cuál es el número de Reynolds R que corresponde a un factor de fricción de Darcy-Weisbach f = 0.03?
-
En un vertedero WES con pendiente aguas abajo de 0.6 H a 1 V, el factor de fricción Darcy-Weisbach es
f = 0.03. Calcule el número de Froude máximo posible para estas condiciones de flujo. -
Asumiendo un número de Froude máximo posible F = 25, calcule el valor de β que asegure el flujo neutralmente estable.
-
Un canal prismático está fluyendo cerca de flujo crítico. La pendiente del fondo es S = 0.004. ¿Cuál es el valor del factor de fricción modificado de Darcy-Weisbach f?
BIBLIOGRAFÍA
|
|
Chow, V. T. 1959. Open-channel Hydraulics. Mc-Graw Hill, New York.
Cornish, V. 1907. Progressive waves in rivers. The Geographical Journal. Vol. 29, No. 1, January, 23-31.
Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, Circular 521, 141-151, National Institute of Standards and Technology, Gaithersburg, Md.
Dooge, J. C. I., W. B. Strupczewski, and J. J. Napiorkoswki. 1982. Hydrodynamic derivation of storage parameters in the Muskingum model. Journal of Hydrology, 54, 371-387.
Fread, D. 1993. "Flow Routing," Chapter 10 in Handbook of Hydrology, D. R. Maidment, editor, McGraw-Hill, New York.
Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.
Lagrange, J. L. de. 1788. Mécanique analytique, Paris, part 2, section II, article 2, p 192.
Lighthill, M. J., y G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
Ponce, V, M., y D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.
Ponce, V. M. 1989. Engineering Hydrology: Principles and Practices. Prentice-Hall, Englewood Cliffs, New Jersey.
Ponce, V. M. 1991a. The kinematic wave controversy. Journal of Hydraulic Engineering, ASCE, Vol. 117, No. 4, April, 511-525.
Ponce, V. M. 1991b. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.
Ponce, V. M., y P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, April, 376-380.
Powell, R. W. 1948. Vedernikov's criterion for ultra-rapid flow. Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.
Seddon, J. A. 1900. River hydraulics. Transactions, ASCE, Vol. XLIII, 179-243, June.
Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid, Dokl. Akad. Nauk SSSR, 48(4), 239-242.
Vedernikov, V. V. 1946. Characteristic features of a liquid flow in an open channel, Dokl. Akad. Nauk SSSR, 52(3), 207-210.
| http://hidraulicadecanales.sdsu.edu |
|
150324 11:15 |